Cauchy-jakauma

Cauchy-jakauma

Tiheysfunktio
Kertymäfunktio
Parametrit	$x_{0}\!$ lokaatio (reaaliluku) γ > 0 skaala (reaaliluku)
Määrittelyjoukko	$\displaystyle x\in (-\infty ,+\infty )\!$
Tiheysfunktio	${\frac {1}{\pi \gamma \,\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\!$
Kertymäfunktio	${\frac {1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}\!$
Odotusarvo	ei ole
Mediaani	$x_{0}\!$
Moodi	$x_{0}\!$
Varianssi	ei ole
Vinous	ei määritelty
Huipukkuus	ei määritelty
Entropia	$\log(\gamma )\,+\,\log(4\,\pi )\!$
Momentit generoiva funktio	ei ole
Karakteristinen funktio	$\displaystyle \exp(x_{0}\,i\,t-\gamma \,|t|)\!$

Cauchy-jakauma (Cauchyn jakauma) on Augustin Cauchyn mukaan nimetty jatkuva todennäköisyysjakauma. Varsinkin fysikaalisissa sovelluksissa sitä nimitetään myös Lorentzin jakaumaksi (Hendrik Lorentzin mukaan), Cauchyn–Lorentzin jakaumaksi tai Breitin–Wignerin jakaumaksi. Yksin­kertaisinta Cauchy-jakaumaa sanotaan standardiksi Cauchy-jakaumaksi. Sen tiheysfunktio on

$f(x;0,1)={\frac {1}{\pi (1+x^{2})}}.\!$

ja sen kertymäfunktio on arkustangenttifunktion muotoinen:

$F(x;0,1)={\frac {1}{\pi }}\arctan \left(x\right)+{\frac {1}{2}}$.

Kahden standardin normaalisti jakautuneen satunnaismuuttujan suhde noudattaa standardia Cauchy-jakaumaa.

Cauchy-jakauma on siitä erikoinen, että sillä ei ole odotusarvoa eikä varianssia. Tämän vuoksi eräät toden­näköisyys­laskennan tärkeät tulokset kuten suurten lukujen laki ja keskeinen raja-arvolause eivät koske Cauchy-jakaumaa noudattavia satunnais­muuttujia. Koska sillä ei ole odotus­arvoa, sillä ei ole myöskään momentit generoivaa funktiota.

Cauchy-jakauma on yksi harvoista vakaista jakaumista, joiden tiheysfunktio voidaan ilmaista analyyttisesti; muita sellaisia ovat normaalijakauma ja Lévyn jakauma.

Historia

Matemaatikot tutkivat Cauchy-jakauman muotoisia funktioita jo 1700-luvun alussa, mutta toisenlaisessa yhteydessä. Tuolloin niistä käytettiin nimitystä Agnesin noita. Jakauman nimestä huolimatta ensimmäisen tutkielman sen ominaisuuksista jakaumana julkaisi ranskalainen matemaatikko Siméon Denis Poisson vuonna 1824; Cauchyn nimi liitettiin siihen vasta erään vuonna 1853 käydyn akateemisen väittelyn yhteydessä. Jakauman nimi on siis esimerkki Stiglerin lain toteutumisesta. Poisson totesi, että jos otetaan keskiarvo tätä jakaumaa noudattavista havainnoista, se ei havaintojen lukumäärän kasvaessa suppene mitään äärellistä lukua kohti. Niinpä Laplace oli tehnyt virheen soveltaessaan keskeistä raja-arvolausetta tällaiseenkin jakaumaan, sillä lause edellyttää äärellistä odotus­arvoa ja varianssia. Poisson ei kuitenkaan pitänyt asiaa kovin tärkeänä, toisin kuin Bienaymé, joka myöhemmin kävi Cauchyn kanssa pitkällisen väittelyn asiasta.

Tilanteita, joissa Cauchy-jakauma esiintyy

Normaalisti jakautuneiden satunnaismuuttujien suhde

Jos U ja V ovat kaksi riippumatonta normaalisti jakautunutta satunnaismuuttujaa, joiden odotusarvo on 0 ja varianssi 1, niiden suhde U/V noudattaa standardia Cauchy-jakaumaa.

Suorien leikkauspisteen jakauma

Oletetaan, että tasolla jonkin x-akselin ulkopuolella olevan pisteen kautta piirretään satunnaisesti valittu suora siten, että tämän suoran suuntakulma on tasaisesti jakautunut välille -π/2 ... ­π/2. Tällöin sen pisteen sijainti, jossa tämä suora leikkaa x-akselin, noudattaa Cauchy-jakaumaa.

Tämä voidaan todistaa seuraavasti:

Olkoon θ kulma, jonka y-akselilla olevan pisteen (0,b) kautta kulkeva suora muodostaa y-akselin kanssa. Jos suora leikkaa x-akselin pisteessä (x₀, 0), on

$\tan \theta ={\frac {x_{0}}{b}}$,

ja

$\theta =\arctan {\frac {x_{0}}{b}}$,

jolloin jos kulma θ on tasaisesti jakautunut välille -π/2; ... π/2;. Leikkaus­pisteen jakauman kertymä­funktion ilmaisee toden­näköisyys, että pisteen x-koordinaatti on pienempi kuin annettu x₀. Näin tapahtuu, jos

$x<x_{0}$

eli jos

$\theta <\theta _{0}=\arctan {\frac {x_{0}}{b}}$

mutta koska θ on tasaisesti jakautunut välille (-π, π), se saa mitä tahansa tällä välillä olevaa arvoa a pienemmän arvon toden­näköisyydellä

${\frac {a}{\pi }}+1/2$,

ja näin ollen arvoa θ₀ pienemmän arvon toden­näköisyydellä

${\frac {1}{\pi }}\arctan {\frac {x_{0}}{b}}+1/2$,

sillä θ saa nollaa pienemmän arvon toden­näköisyydellä 1/2.

Kyseisen leikkauspisteen sijainnin x-koordinaatin arvo on siis satunnaismuuttuja, jonka kertymä­funktio on

${\frac {1}{\pi }}\arctan {\frac {x}{b}}$

mikä on juuri Cauchy-jakauman Cauchy (0,1) kertymäfunktio.

Jakauman tiheys- ja kertymäfunktio

Tiheysfunktio

Cauchy-jakauman tiheysfunktio on

$f(x;x_{0},\gamma )={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}={1 \over \pi \gamma }\left[{\gamma ^{2} \over (x-x_{0})^{2}+\gamma ^{2}}\right],$

missä parametri x₀ (lokaatioparametri) osoittaa jakauman huipun sijainnin ja γ (skaalaparametri) osoittaa jakauman leveyden, tai tarkemmin sanottuna, millä etäisyydellä jakauman huipusta tiheys­funktion arvo on puolet tästä maksimi­arvosta. Samalla γ on myös puolet jakauman ylä- ja ala­kvartiilien erotuksesta, ja sitä sanotaan joskus todennäköiseksi virheeksi. Augustin-Louis Cauchy käytti vuonna 1827 tästä tiheys­funktiosta sellaistakin muunnosta, jossa skaala­parametri oli infinitesimaalinen, ja täten hän tuli määritellyksi sen, mitä nykyisin sanotaan Diracin deltafunktioksi.

Tiheysfunktion suurin arvo eli jakauman amplitudi on

${\text{Amplitudi}}={\frac {1}{\pi \gamma }}.$

Siinä erikois­tapauksessa, että x₀ = 0 ja γ = 1 saadaan standardi Cauchy-jakauma, jonka tiheysfunktio on

$f(x;0,1)={\frac {1}{\pi (1+x^{2})}}.\!$

Fysiikassa käytetään usein kolmi­parametrista Lorentzin funktiota:

$f(x;x_{0},\gamma ,I)={\frac {I}{\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}=I\left[{\gamma ^{2} \over (x-x_{0})^{2}+\gamma ^{2}}\right],$

missä I on huipun korkeus. Tämä kolmi­parametrinen Lorentzin funktio ei yleensä ole toden­näköisyys­tiheys­funktio, sillä sen integraali ei ole 1 paitsi siinä erikois­tapauksessa, että $I={\frac {1}{\pi \gamma }}.\!$.

Kertymäfunktio

Cauchy-jakauman kertymäfunktio on:

$F(x;x_{0},\gamma )={\frac {1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}$

ja sen kvantiilifunktio eli kertymä­funktion käänteisfunktio on

$Q(p;x_{0},\gamma )=x_{0}+\gamma \,\tan \left[\pi \left(p-{\tfrac {1}{2}}\right)\right].$

Tästä seuraa, että jakauman ala- ja ylä­kvartiilit ovat x₀-γ ja x₀+γ),

ja kvartiilien erotus näin ollen 2γ.

Cauchy-jakauman kvantiili­funktion derivaatta eli jakauman kvantiili­tiheys­funktio on:

$Q'(p;\gamma )=\gamma \,\pi \,{\sec }^{2}\left[\pi \left(p-{\tfrac {1}{2}}\right)\right].\!$

Jakauman differentiaalinen entropia määritellään sen kvantiili­tiheys­funktion avulla:, nimittäin

$h(\gamma )=\int _{0}^{1}\log \,(Q'(p;\gamma ))\,\mathrm {d} p=\log(\gamma )\,+\,\log(4\,\pi ).\!$

Ominaisuuksia

Cauchy-jakauman (eli Lorentz-jakauman) ja Gaussin normaalijakauman tiheysfunktioiden vertailu, josta ilmenevät edellisen paksummat "hännät".

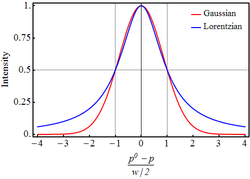
Cauchy-jakauma on esimerkki jakaumasta, jolla ei ole odotusarvoa, varianssia eikä korkeampia momentteja. Sen sijaan sillä kyllä on hyvin määritelty moodi eli tiheys­funktion maksimi­kohta ja mediaani, jotka molemmat ovat suuruudeltaan x₀. Jakauman tiheys­funktion kuvaaja on lisäksi symmetrinen tämän mediaanin suhteen ja muistuttaa muodoltaan normaalijakauman kuvaajaa eli Gaussin käyrää, mutta ei silti toteuta odotus­arvon määritelmän ehtoja. Cauchy-jakauman tiheysfunktio lähestyy kummassakin päässä nollaa oleellisesti hitaammin kuin normaalijakauman; sanotaan, että sillä on paksummat "hännät".

Jos X₁, ..., X_n ovat riippumattomia ja identtisesti jakautuneita satunnais­muuttujia, joista jokainen noudattaa standardia Cauchy-jakaumaa, niiden otos­keski­arvo (X₁+ ... +X_n)/n noudattaa samaa standardia Cauchyn jakaumaa. Tämä voidaan osoittaa laskemalla keskiarvon karakteristinen funktio:

$\phi _{\overline {X}}(t)=\mathrm {E} \left[e^{i{\overline {X}}t}\right]$

missä ${\overline {X}}$ on otos­keski­arvo. Keskeinen raja-arvolause ei siis päde Cauchy-jakaumalle, mutta sillä ei olekaan lauseen edellyttämää äärellistä varianssia, ja näin ollen tämä esimerkki osoittaa, että tämä todella on oleellinen edellytys, jota ei voida jättää huomioon ottamatta. Myöskään suurten lukujen laki ei koske Cauchy-jakaumaa, koska sillä ei ole odotus­arvoa. Cauchy-jakauma on täysin vakaa jakauma.

Standardi Cauchy-jakauma saadaan myös erikois­tapauksena Studentin t-jakaumasta, kun vapausasteita on yksi.

Kuten kaikkien muidenkin vakaiden jakaumien tapauksessa, se lokaatio-skaala-perhe, johon Cauchy-jakauma kuuluu, on suljettu sellaisten lineaaristen muunnosten suhteen, joiden kertoimet ovat reaalilukuja. Lisäksi jakauma­perhe on suljettu reaali­kertoimisten lineaaristen frationaalisten muunnosten suhteen.

Karakteristinen funktio

OlkoonX Cauchy-jakautunut satunnais­muuttuja. Jakauman karakteristinen funktio on

$\phi _{X}(t;x_{0},\gamma )=\mathrm {E} \left[e^{iXt}\right]=\int _{-\infty }^{\infty }f(x;x_{0},\gamma )e^{ixt}\,dx=e^{ix_{0}t-\gamma |t|}.$

mikä on samalla tiheysfunktion Fourier-muunnos. Alkuperäinen toden­näköisyy­stiheys voidaan esittää karakteristisen funktion avulla oleellisesti käyttämällä käänteistä Fourier-muunnosta:

$f(x;x_{0},\gamma )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\phi _{X}(t;x_{0},\gamma )e^{-ixt}\,dt\!$

On huomattava, että karakteristinen funktio ei ole differentioituva origossa: tämä vastaa sitä, että Cauchy-jakaumalla ei ole odotusarvoa.

Miksi odotusarvoa ja momentteja ei voida määrittää

Odotusarvo

Jos todennäköisyysjakaumalla on tiheysfunktio f(x), sen odotusarvo on

$\int _{-\infty }^{\infty }xf(x)\,dx.\qquad \qquad (1)\!$

Kysymys on nyt siitä, miten määritellään integraali molemmista päistä rajoittamattoman välin yli: onko se sama kuin

$\int _{a}^{\infty }xf(x)\,dx+\int _{-\infty }^{a}xf(x)\,dx.\qquad \qquad (2)\!$

jokaisella mieli­valtaisella reaali­luvulla a.

Jos ainakin toinen lausekkeen (2) yhteen­laskettavista on äärellinen, lausekkeet (1) ja (2) ovat yhtä suuret. Mutta Cauchy-jakauman tapauksessa edellinen näistä yhteen­laskettavista on miinus ääretön, jälkimmäinen plus ääretön, eikä niiden summaa voida laskea. Sen vuoksi lauseke (1) ei ole määritelty, eikä Cauchyn jakaumalla sen vuoksi ole odotusarvoa.

Vaikuttaisi ehkä luonnolliselta käsittää lauseke (1) raja-arvoksi

$\lim _{a\to \infty }\int _{-a}^{a}xf(x)\,dx,\!$.

Tämä raja-arvo, niin sanottu Cauchyn perusarvo, on nolla. Mutta lausekkeen (1) voitaisiin yhtä hyvin tulkita tarkoittavan myös esimerkiksi raja-arvoa

$\lim _{a\to \infty }\int _{-2a}^{a}xf(x)\,dx,\!$

joka ei ole nolla, mikä voidaan todeta suorittamalla integrointi.

Monet odotus­arvoa koskevat toden­näköisyys­laskennan tulokset kuten vahva suurten lukujen laki eivät tällaisissa tapauksissa päde.

Korkeammat momentit

Cauchy-jakaumalla ei ole minkään asteen äärellisiä momentteja. Jotkin korkeammista raaoista momenteista sillä kyllä on, ja ne ovat äärettömiä, esimerkiksi raaka toinen momentti:

${\begin{aligned}\mathrm {E} [X^{2}]&\propto \int _{-\infty }^{\infty }{\frac {x^{2}}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }1-{\frac {1}{1+x^{2}}}\,dx\\[8pt]&=\int _{-\infty }^{\infty }dx-\int _{-\infty }^{\infty }{\frac {1}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }dx-\pi =\infty .\end{aligned}}$

Järjestämällä lauseke uudestaan huomataan, että toinen momentti on oleellisesti vakion, tässä luvun 1, integraali äärettömän välin yli. Myös korkeammat parillisen potenssin raa'at momentit saavat arvon ääretön. Parittoman potenssin raakoja momentteja taas ei voida lainkaan määritellä. Ne nimittäin olisivat oleellisesti sama asia kuin lauseke $\infty -\infty$, sillä lausekkeessa olevat kaksi integraalia, joista toinen vähennetään toisesta, ovat molemmat äärettömiä. Ensimmäinen raaka momentti on sama kuin jakauman odotusarvo, jota tässä tapauksessa ei siis myöskään voida määritellä. Tämä taas merkitsee, että jakaumalle ei voida määritellä myöskään keskeisiä momentteja eikä standardoituja momentteja, sillä ne kaikki määritellään odotusarvon avulla. Samasta syystä Cauchy-jakaumalla ei ole myöskään varianssia, sillä se on sama kuin toinen keskeinen momentti, vaikka sillä onkin toinen raaka momentti, joka on ääretön.

Korkeampia momentteja koskevat tulokset seuraavat Hölderin epäyhtälötä, jonka mukaan alempien momenttien hajaantuessa korkeammatkin momentit hajaantuvat.

Parametrien estimointi

Koska Cauchyn jakauman parametrit eivät vastaa odotusarvoa ja varianssia, Cauchy-jakauman parametreja ei voida estimoida otoksen keskiarvon ja varianssin avulla. Jos esimerkiksi otetaan Cauchy-jakauman mukaisesta aineistosta n otosta, tämän otoksen keskiarvo voidaan laskea:

${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$

Vaikka otoksen arvot x_i keskittyvät lähelle mediaania x₀, otoksen keskiarvo voi vaihdella yhä enemmän sitä mukaa kuin lisää otoksia poimitaan, koska on yhä todennäköisempää, että kohdataan tapauksia, jotka poikkeavat siitä paljon. Itse asiassa otosten keskiarvo noudattaa samaa jakaumaa kuin otokset itsekin, toisin sanoen suuren otoksen keskiarvo ei ole lainkaan parempi, joskaan ei huonompikaan arvio mediaanille x₀ kuin mikään yksittäinen otokseen kuuluva havaintokaan. Samoin myös otoksen varianssi kasvaa yhä suuremmaksi, kun lisää otoksia poimitaan.

Siksi mediaanin x₀ ja skaalaparametrin γ arvioimiseksi tarvitaan vahvempia menetelmiä. Muuan yksinkertainen keino on käyttää otoksen mediaania x₀:n estimaattorina sekä ala- ja yläkrvartiilin erotusta estimaattorina γ:lle. Muitakin, tarkempia ja vahvempia menetelmiä on keksitty. Esimerkiksi katkaistu keskiarvo otoksen järjestystilaston keskimmäisistä 24 prosentista tapauksia antaa x₀:lle arvion tehokkaammin kuin koko otoksen mediaani. Kun Cauchy-jakauma kuitenkin on ääripäistään "paksu" eli sen tiheysfunktio lähestyy kummassakin päässä vain hitaasti nollaa, arvion tehokkuus alenee, kun otoskoko ylittää 24 %.

Parametrin x₀ and γ arviointiin voidaan käyttää myös suurimman uskottavuuden estimointia. Se on yleensä kuitenkin hankalaa, koska sitä varten on ratkaistava korkeamman asteen polynomiyhtälö, ja sillä voi olla useita ratkaisuja, jotka vastaavat korkeamman asteen polynomiyhtälön juuret, ja sillä voi olla useita juuria, jotka vastaavat lokaaleja maksimikohtia. Lisäksi vaikka suurimman uskottavuuden estimointi onkin asymptoottisesti tehokas, pienillä otoksilla se on melko tehoton. Otoskoolla n Cauchy-jakauman logaritminen todennäköisyysfunktio on:

${\hat {\ell }}(\!x_{0},\gamma \mid x_{1},\dotsc ,x_{n})=-n\log(\gamma \pi )-\sum _{i=1}^{n}\log \left(1+\left({\frac {x_{i}-x_{0}}{\gamma }}\right)^{2}\right)$

Maksimoimalla logaritminen todennäköisyysfunktio x₀:n ja γ:n suhteen saadaan seuraava yhtälöryhmä:

$\sum _{i=1}^{n}{\frac {x_{i}-x_{0}}{\gamma ^{2}+[x_{i}-\!x_{0}]^{2}}}=0$

$\sum _{i=1}^{n}{\frac {\gamma ^{2}}{\gamma ^{2}+[x_{i}-x_{0}]^{2}}}-{\frac {n}{2}}=0$

On huomattava, että

$\sum _{i=1}^{n}{\frac {\gamma ^{2}}{\gamma ^{2}+[x_{i}-x_{0}]^{2}}}$

on γ:n monotoninen funktio ja että ratkaisun γ täytyy toteuttaa epäyhtälö

$\min |x_{i}-x_{0}|\leq \gamma \leq \max |x_{i}-x_{0}|.$

Pelkän x₀:n ratkaiseminen edellyttää 2n-1:nnen asteen polynomiyhtälön ratkaisemista, ja pelkän γn ratkaiseminen n:nnen asteen polynomiyhtälön ratkaisemista (ensin γ²:n, sitten x₀:n). Siksi yleensä onkin käytettävä tietokoneella suoritettavia numeerisen analyysin menetelmiä, olipa tarkoituksena ratkaista molemmat parametrit tai vain toinen niistä. Suurimman uskottavuuden estimoinnin etuna on asymptoottinen tehokkuus; x₀:n estimointi otoksen mediaanin avulla on vain 81-prosenttisesti niin tehokas kuin sen estimointi suurimman uskottavuuden menetelmällä. Katkaistun otoskeskiarvon menetelmä 24 prosentin järjestystilastolla on asymptoottisesti noin 88-prosenttisesti niin tehokas kuin x₀:n estimointi suurimman uskottavuuden menetelmällä. Menetelmiä voidaan myös yhdistää etsimällä keskimmäisten 24 prosentin järjestystilastolla x₀ jokin alustava likiarvo, jota sitten parannetaan suurimman uskottavuuden estimaattoreilla soveltamalla Newtonin menetelmää.

Moniulotteinen Cauchy-jakauma

Satunnaisvektorin X = (X₁, ..., X_k)' sanotaan noudattavan moniulotteista Cauchy-jakaumaa, jos sen komponenttien jokainen lineaarikombinaatio Y = a₁X₁ + ... + a_kX_k noudattaa Cauchy-jakaumaa. Toisin sanoen jokaisen vakiovektorin $a\in \mathbb {R} ^{k}$ ja satunnaisvektorin X pistetulo a · X noudattaa tavallista (yksiulotteista) Cauchy-jakaumaa. Moniulotteisen Cauchy-jakauman karakteristinen funktio on

$\phi _{X}(t)=e^{ix_{0}(t)-\gamma (t)},\!$

missä x₀(t) ja γ(t) ovat reaalifunktioita, joilla x₀(t) on ensimmäisen asteen homogeeninen funktio ja γ(t) positiivinen homogeeninen ensimmäisen asteen funktio. Täsmällisemmin sanottuna:

$x_{0}(at)=ax_{0}(t),$

$\gamma (at)=|a|\gamma (t),$

kaikilla t.

Esimerkki bivariaattisesta Cauchy-jakaumasta saadaan lausekkeella:

$f(x,y;x_{0},y_{0},\gamma )={1 \over 2\pi }\left[{\gamma \over ((x-x_{0})^{2}+(y-y_{0})^{2}+\gamma ^{2})^{1.5}}\right].$

Vaikka tämä esimerkki ei olekaan analoginen kovariantin matriisin kanssa, voidaan todeta, että x ja y eivät ole riippumattomia.

Analogisesti tavallisen yksiulotteisen tiheysfunktion kanssa myös moniulotteinen Cauchyn tiheysfunktio liittyy läheisesti moniulotteiseen Studentin jakaumaan. Jos viimeksi mainitun vapausasteluku on 1, kyseessä on sama kuin moniulotteisen Cauchy-jakauma. Ja k-ulotteisen Studentin jakauman tiheysfunktio yhdellä vapausasteella on:

$f({\mathbf {x} };{\mathbf {\mu } },{\mathbf {\Sigma } },k)={\frac {\Gamma \left({\frac {1+k}{2}}\right)}{\Gamma ({\frac {1}{2}})\pi ^{\frac {k}{2}}\left|{\mathbf {\Sigma } }\right|^{\frac {1}{2}}\left[1+({\mathbf {x} }-{\mathbf {\mu } })^{T}{\mathbf {\Sigma } }^{-1}({\mathbf {x} }-{\mathbf {\mu } })\right]^{\frac {1+k}{2}}}}.$

Muunnosominaisuudet

• Jos $X\sim {\textrm {Cauchy}}(x_{0},\gamma )\,$, niin $kX+l\sim {\textrm {Cauchy}}(x_{0}{k}+l,\gamma |k|)\,$
• Jos $X\sim {\textrm {Cauchy}}(x_{0},\gamma _{0})\,$ ja $Y\sim {\textrm {Cauchy}}(x_{1},\gamma _{1})\,$ ovat riippumattomia, niin $X+Y\sim {\textrm {Cauchy}}(x_{0}+x_{1},\gamma _{0}+\gamma _{1})\,$
• Jos $X\sim {\textrm {Cauchy}}(0,\gamma )\,$, niin ${\tfrac {1}{X}}\sim {\textrm {Cauchy}}(0,{\tfrac {1}{\gamma }})\,$
• McCullaghin parametraatio Cauchy-jakaumalle: Jos Cauchy-jakauman ilmaiseminen kompleksiparametrin $\psi =x_{0}+i\gamma$, voidaan märitellä, että X ~ Cauchy(ψ), jos X ~ Cauchy$(x_{0},|\gamma |)$. Jos X ~ Cauchy(ψ) niin:

${\frac {aX+b}{cX+d}}$ ~ Cauchy$\left({\frac {a\psi +b}{c\psi +d}}\right)$

missä a,b,c ja d ovat reaalilukuja.

• Jos X ~ Cauchy(ψ) edellä esitetyn määritelmän mukaisessa mielessä, niin

${\frac {X-i}{X+i}}$ ~ CCauchy$\left({\frac {\psi -i}{\psi +i}}\right)$

missä "CCauchy" on sirkulaarinen Cauchy-jakauma.

Suhde muihin jakaumiin

• ${\textrm {Cauchy}}(0,1)$ on sama kuin ${\textrm {t}}(df=1)\,$ Studentin t-jakauma
• ${\textrm {Cauchy}}(\mu ,\sigma )$ on sama kuin ${\textrm {t}}_{(df=1)}(\mu ,\sigma )\,$, ei-standardoitu Studentin t-jakauma
• Jos $X,Y\sim {\textrm {N}}(0,1)$ ja X ja Y ovat riippumattomia, niin ${\tfrac {X}{Y}}\sim {\textrm {Cauchy}}(0,1)\,$
• Jos $X\sim {\textrm {U}}(0,1)\,$ niin $\tan \left({\pi \left(X-{\tfrac {1}{2}}\right)}\right)\sim {\textrm {Cauchy}}(0,1)\,$
• Jos X ~ Log-Cauchy(0, 1) niin ln(X) ~ Cauchy(0, 1)
• Cauchy-jakauma on rajatapaus tyypin 4 Pearsonin jakaumasta^lähde?
• Cauchy-jakauma on erikoistapaus tyypin 7 Pearsonin jakaumasta
• Cauchy-jakauma on hyperbolisen jakauman singulaarinen raja-arvo

Aiheesta muualla

• Cauchy distribution Encyclopedia of Mathematics. Viitattu 13.1.2016.
• GNU Scientific Library – Reference Manual: 20.8: The Cauchy Distribution gnu.org. Viitattu 13.1.2016.
• Ratios of Normal Variables George Marsaglia. Viitattu 13.1.2016.

Todennäköisyysjakaumat

Diskreettejä jakaumia	Bernoullin jakauma Binomijakauma Geometrinen jakauma Hypergeometrinen jakauma Negatiivinen binomijakauma Poissonin jakauma
Jatkuvia jakaumia	Beta-jakauma Cauchy-jakauma Eksponenttijakauma F-jakauma Gamma-jakauma Khii toiseen -jakauma Log-normaalijakauma Normaalijakauma Pareto-jakauma Studentin t-jakauma Tasajakauma Weibull-jakauma
Moniulotteisia jakaumia	Dirichlet-jakauma Moniulotteinen Studentin t-jakauma Multinomijakauma Multinormaalijakauma