Negatiivinen binomijakauma
Todennäköisyysfunktio
r
=
10.
{\displaystyle r=10.}
p
=
0.2
{\displaystyle p=0.2}
p
=
0.5
{\displaystyle p=0.5}
p
=
0.8
{\displaystyle p=0.8}
Merkintä
N
B
(
r
,
p
)
{\displaystyle \mathrm {NB} (r,\,p)}
Parametrit
r > 0 odotettu onnistumiskertap ∈ (0,1) onnistumisen todennäköisyys
Määrittelyjoukko
k ∈ { 0, 1, 2, 3, … } (epäonnistumisten lukumäärä)
Pistetodennäköisyysfunktio
(
k
+
r
−
1
k
)
⋅
p
r
(
1
−
p
)
k
{\displaystyle {k+r-1 \choose k}\cdot p^{r}(1-p)^{k}}
Kertymäfunktio
1
−
I
1
−
p
(
k
+
1
,
r
)
{\displaystyle 1-I_{1-p}(k+1,\,r)}
Odotusarvo
r
(
1
−
p
)
p
{\displaystyle {\frac {r(1-p)}{p}}}
Moodi
⌊
(
1
−
p
)
(
r
−
1
)
p
⌋
{\displaystyle \left\lfloor {\frac {(1-p)(r-1)}{p}}\right\rfloor }
Varianssi
r
(
1
−
p
)
p
2
{\displaystyle {\frac {r(1-p)}{p^{2}}}}
Vinous
2
−
p
r
(
1
−
p
)
{\displaystyle {\frac {2-p}{\sqrt {r(1-p)}}}}
Huipukkuus
6
r
+
p
2
r
(
1
−
p
)
{\displaystyle {\frac {6}{r}}+{\frac {p^{2}}{r(1-p)}}}
Momentit generoiva funktio
(
p
e
s
1
−
(
1
−
p
)
e
s
)
r
,
s
<
|
ln
(
1
−
p
)
|
{\displaystyle \left({\frac {pe^{s}}{1-(1-p)e^{s}}}\right)^{r}\!\!\!,s<|\ln(1-p)|}
Karakteristinen funktio
(
p
e
i
s
1
−
(
1
−
p
)
e
i
s
)
r
{\displaystyle \left({\frac {pe^{\mathrm {i} s}}{1-(1-p)e^{\mathrm {i} s}}}\right)^{r}}
Todennäköisyydet generoiva funktio
(
1
−
p
1
−
p
z
)
r
für alle
|
z
|
<
1
p
{\displaystyle {\biggl (}{\frac {1-p}{1-pz}}{\biggr )}^{\!r}{\text{ für alle }}|z|<{\frac {1}{p}}}
Negatiivinen binomijakauma on dikotomisen toistokokeen mielivaltaisen monennetta onnistumista edeltävien yritysten jakauma .
Negatiivinen binomijakauma on diskreetti ja sen arvojoukko on luonnollisten lukujen joukko . Jos satunnaismuuttuja
X
{\displaystyle X}
negatiivisbinomijakautunut , merkitään
X
∼
Negbin
(
r
,
p
)
.
{\displaystyle X\sim \operatorname {Negbin} (r,p).}
Jakauman parametri
0
≤
p
≤
1
{\displaystyle 0\leq p\leq 1}
r
∈
N
{\displaystyle r\in \mathbb {N} }
Pistetodennäköisyysfunktio on
P
(
X
=
i
)
=
(
r
+
i
−
1
i
)
p
r
(
1
−
p
)
i
.
{\displaystyle \operatorname {P} (X=i)={r+i-1 \choose i}p^{r}(1-p)^{i}.}
Odotusarvo ja varianssi ovat
E
(
X
)
=
r
(
1
−
p
)
p
{\displaystyle \operatorname {E} (X)={\frac {r(1-p)}{p}}}
Var
(
X
)
=
r
(
1
−
p
)
p
2
.
{\displaystyle \operatorname {Var} (X)={\frac {r(1-p)}{p^{2}}}.}
Jos
X
1
∼
Negbin
(
r
1
,
p
)
{\displaystyle X_{1}\sim \operatorname {Negbin} (r_{1},p)}
X
2
∼
Negbin
(
r
2
,
p
)
{\displaystyle X_{2}\sim \operatorname {Negbin} (r_{2},p)}
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
1
+
X
2
∼
Negbin
(
r
1
+
r
2
,
p
)
{\displaystyle X_{1}+X_{2}\sim \operatorname {Negbin} (r_{1}+r_{2},p)}
Negatiivisen binomijakauman yhteys geometriseen jakaumaan on
Negbin
(
1
,
p
)
=
Geom
(
p
)
.
{\displaystyle \operatorname {Negbin} (1,p)=\operatorname {Geom} (p).}
Jakauman nimi tulee pistetodennäköisyysfunktion samankaltaisuudesta binomijakaumaan , ja siitä että pistetodennäköisyysfunktion voi ilmaista negatiivisen binomikertoimen avulla
P
(
X
=
i
)
=
(
−
r
i
)
p
r
(
−
(
1
−
p
)
)
i
.
{\displaystyle \operatorname {P} (X=i)={-r \choose i}p^{r}(-(1-p))^{i}.}
Diskreettejä jakaumia Jatkuvia jakaumia Moniulotteisia jakaumia
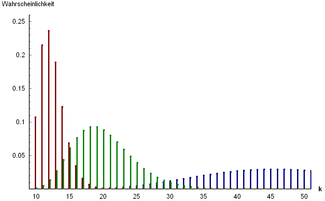 Pistetodennäköisyysfunktiot, kun
Pistetodennäköisyysfunktiot, kun 




























