Uniforminen monitahokas

Tetraedri kuuluu Platonin kappaleisiin.

Pullistettu dodekaedri kuuluu uniformisiin tähtimonitahokkaisiin.

Uniforminen monitahokas on monitahokas, jonka kaikki sivutahkot ovat säännöllisiä monikulmioita ja joka on kärkitransitiivinen, toisin sanoen se voidaan aina kuvata yhtenevyyskuvauksella itselleen siten, että mikä tahansa kärki voidaan kuvata mille tahansa toiselle. Tästä seuraa, että sen kaikki kärjet ovat yhtenevät.

Uniforminen monitahokas voi olla joko

• säännöllinen (jos se on myös tahko- ja särmätransitiivinen)
• kvasisäännöllinen (jos se on myös särmätransitiivinen mutta ei tahkotransitiivinen), tai
• semiregulaarinen (jos se ei ole tahko- eikä särmätransitiivinen).

Uniformisen monitahokkaan ei tarvitse olla kupera, joten monet uniformiset monitahokkaat ovat samalla tähtimonitahokkaita.

On olemassa kaksi ääretöntä uniformisten monitahokkaiden luokkaa sekä lisäksi vielä 75 näihin luokkiin kuulumatonta uniformista monitahokasta:

• Äärettömät luokat:
  • särmiöt eli prismat
  • antiprismat
• Muut kuperat:
  • 5 Platonin kappaletta – säännölliset kuperat monitahokkaat
  • 13 Arkhimedeen kappaleta – 2 kvasisäännöllistä ja 11 semiregulaarista kuperaa monitahokasta
• Tähtimonitahokkaat:
  • 4 Kepler-Poinsotin kappaletta – säännölliset ei-kuperat monitahokkaat
  • 53 uniformista tähtitahokasta – 5 kvasisäännöllistä ja 48 semiregulaarista,

Lisäksi on olemassa myös joukko degeneroituja uniformisia monitahokkaita, joissa osa särmistä yhtyy toisiinsa, muun muassa yksi John Skillingin löytämä, jota sanotaan suureksi kaksoispullistetuksi dirombidodekaedriksi eli Skillingin kuvioksi.

Uniformisten monitahokkaiden duaalikappaleet ovat sivutransitiivisia eli isoedrisiä, ja niiden kärkikuviot ovat säännöllisiä monikulmioita. Ne luokitellaan usein rinnakkain uniformisten duaalikappaleidensa kanssa. Säännöllisen monitahokkaan duaalikappale on säännöllinen, kun taas Arkhimedeen kappaleiden duaalit ovat Catalanin kappaleita.

Uniformisen monitahokkaan käsite on erikoistapaus uniformisen polytoopin käsitteestä, joka soveltuu myös muotoihin korkeampi- tai alempiulotteisessa avaruudessa.

Määritelmä

Coxeter, Longuet-Higgins ja Miller määrittelivät vuonna 1954 uniformiset monitahokkaat kärkitransitiivisiksi monitahokkaiksi, joiden sivut ovat säännöllisiä monikulmioita. Monitahokkaan he määrittelivät sellaiseksi äärelliseksi joukoksi monikulmioita, että jokainen monikulmion sivu on tasan yhden toisenkin monikulmion sivuna, niin että millään monikulmioiden ei-tyhjällä aidolla osajoukolla ei ole samaa ominaisuutta. Monikulmiolla he impilisiittisesti tarkoittivat kolmiulotteisessa euklidisessa avaruudessa olevaa monikulmiota; niiden sallitaan olla ei-kuperia ja leikata toisensa.

Uniformisen monitahokkaan käsitettä on erinäisillä tavoilla yleistetty. Jos ei edellytetä, että sellaisen on oltava yhtenäinen, voidaan myös useamman komponentin, esimerkiksi viiden kuution yhdistelmää pitää uniformisena. Jos ei edellytetä, että monitahokkaan on oltava degeneroitumaton, saadaan myös niin sanottuja degeneroituja uniformisia monitahokkaita. Tämä edellyttää, että monitahokkaan käsite on määriteltävä yleisemmin.

Branko Grünbaum kiinnitti vuonna 1994 julkaisemassaan artikkelissa huomiota siihen, että vaikka jo Eukleides luetteli viisi säännöllistä monitahokasta ja myöhemmin muun muassa Kepler, Poinsot, Hess ja Brückner olivat eri tavoin luokitelleet monitahokkaita, kukaan heistä ei ollut esittänyt itse monitahokkaan käsitteelle täsmällistä ja yksikäsitteistä määritelmää. Samassa artikkelissa hän itse esitti käsitteelle jokseenkin monimutkaisen määritelmän.

McMullen ja Schulte esittivät vuonna 2003 monitahokkaan käsitteelle yleisemmän määritelmän. Heidän mukaansa monitahokas on kaksiulotteinen abstrakti polytooppi, jolla on ei-degeneroitunut kolmiulotteinen realisaatio. Tässä abstrakti polytooppi on sen sivutahkojen yhdistelmä, joka toteuttaa useita ehtoja, ja realisaatio on kuvaus sen kärkien joukosta johonkin avaruuteen, ja realisaatiota sanotaan ei-degeneroituneeksi, jos millä tahansa kahdella abstraktin polytoopin tahkolla on erilliset realisaatiot.

Monitahokas voi olla degeneroitunut esimerkiksi seuraavilla tavoilla:

• Kätketyt tahkot. Joillakin monitahokkailla osa tahkoista voi olla kätkettyjä siinä mielessä, ettei mikään niiden sisäpiste näy ulkopuolelta. Sellaisia ei yleensä pidetä uniformisina monitahokkaina.
• Degeneroidut komponentit. Monitahokas saattaa koostua useammasta melkein toisistaan erillään olevasta komponentista, jolla kuitenkin on yksi tai useampi yhteinen särmä. Yhtenäisten särmien vuoksi monitahokas on tällöin kuitenkin topologisessa mielessä yhtenäinen.
• Kaksinkertaiset peitteet. On olemassa suunnistumattomia monitahokkaita, joilla on kaksoispeite ja ja jotka täyttävät uniformisen monitahokkaan määritelmän ehdot. Näillä kaksoispeitteillä on kaksinkertaisia tahkoja, särmiä ja kärkiä. Niitä ei yleensä lueta uniformisiin monitahokkaisiin.
• Kaksinkertaiset tahkot. On useita monitahokkaita, joilla on Wythoffin konstruktiolla aikaansaatuja kaksinkertaisia tahkoja. Useimmat kirjoittajat eivät salli kaksinkertaisia tahkoja ja poistavat ne osana konstruktiota.
• Kaksinkertaiset särmät. Skillingin kuviolla on kaksinkertaisia särmiä, kuten degeneroituneilla uniformisilla monitahokkaillakin, mutta niiden tahkoja ei muodostaa kirjoittaa kahden uniformisen monitahokkaan yhdisteenä.

Historia

Säännölliset kuperat monitahokkaat:

• Säännölliset monitahokkaat eli Platonin kappaleet tunnettiin jo antiikin Kreikassa, ja niitä tutkivat pythagoralaiset, Platon (n. 424–348 eKr.), Theaitetos (n. 417–369 eKr.), Timaios Lokroilainen n. 420–380 eKr.) ja Eukleides (noin 300 eKr.). Säännöllisen dodekaedrin keksivät etruskit ennen vuotta 500 eKr.

Ei-säännölliset uniformiset kuperat monitahokkaat:

• Kuboktaedrin tunsi jo Platon.
• Arkhimedes (287–212 eKr.) löysi kaikki 13 Arkhimedeen kappaletta. Hänen oma teoksensa aiheesta on kadonnut, mutta Pappos Aleksandrialainen (n. 290–350 jKr.) mainitsee Arkhimedeen luetelleen 13 monitahokasta.
• Piero della Francesca (1415–1492) löysi uudelleen Platonin kappaleiden viisi typistettyä muunnosta: typistetyn tetraedrin, typistetyn oktaedrin, typistetyn kuution, typistetyn dodekaedrin ja typistetyn ikosaedrin.
• Luca Pacioli julkaisi Francescan tutkimukset vuonna 1509 uudestaan teoksessaan De divina proportione. Siinä hän lisäsi joukkoon Leonardo da Vincin kuvaaman rombikuboktaedrin, jota hän sanoi ikosiheksaedriksi, koska siinä oli 26 tahkoa.
• Johannes Kepler (1571–1630) julkaisi vuonna 1619 ensimmäisenä täydellisen luettelon Arkhimedeen kappaleista ja tunnisti uniformisten särmiöiden ja antiprismojen äärettömät perheet.

Säännölliset tähtimonitahokkaat:

• Kepler löysi vuonna 1619 kaksi säännöllisistä Kepler–Poinstotin kappaleista ja Louis Poinsot vuonna 1809 kaksi muuta. Augustin Cauchy (1789–1857) todisti, ettei tällaisia kappaleita ole enempää kuin jo tunnetut neljä, ja nimen niille antoi Arthur Cayley (1821–1895).

Muut 53 ei-säännöllistä tähtimonitahokasta:

• Jäljellä olevista 53 uniformisesta monitahokkaasta Edmund Hess löysi kaksi vuonna 1878, Albert Badoureau 36 lisää vuonna 1881. Vuonna 1881 Pitsch löysi heistä riippumatta 18 tällaista monitahokasta, joista kolme oli ennen tuntemattomiua. Kaikkiaan näistä tunnettiin sen jälkeen 41.
• Geometrikko H.S.M. Coxeter löysi loput 12 uniformista tähtimonitahokasta yhteistyössä J. C. P. Millerin (1930–1932) kanssa, mutta ei julkaissut tutkimuksiaan. M.S. Longuet-Higgins ja H.C. Longuet-Higgins löysivät itsenäisesti niistä 11. Lesavre ja Mercier löysivät niistä viisi uudestaan vuonna 1947.
• H. S. M. Coxeter, M. S. Longuet-Higgins ja J. C. P. Miller julkaisivat vuonna 1954 luettelon tuntemistaan uniformisista monitahokkaista
• S. P. Sopov todisti vuonna 1970, että edellä mainittujen esittämä luettelo on täydellinen eli että enempää uniformisia monitahokkaita ei ole.
• Vuonna 1974, Magnus Wenninger julkaisi teoksen Polyhedron models, jossa hän luetteli kaikki 75 ei-prismaattista uniformista monitahokasta. Monilla niistä oli ennen julkaisemattomat nimet, jotka niille antoi Norman Johnson.
• J. Skilling todisti vuonna 1975 edeltäjistään riippumatta, että luettelo oli täydellinen, ja osoitti, että jos uniformisen monitahokkaan määritelmää väljennetään siten, että särmät saavat yhtyä toisiinsa, tällaisia monitahokkaita saadaan vain yksi lisää.
• Vuonna 1987 Edmond Bonan piirsi kaikki uniformiset monitahokkaat ja niiden duaalikappaleet Turbo Pascal -ohjelmalla nimeltä Polyca. Melkein kaikki niistä näytettiin Eastbournen kongressiteatterissa, Britanniassa pidetyssä International Stereoscopic Unionin kongressissa.
• Vuonna 1993 Zhi Har'El muodosti täydelliset kaleidoskooppiset konstruktiot uniformisille monitahokkaille ja niiden duaalikappaleille Kaleido- nimisellä tietokoneohjelmalla ja teki asiasta yhteenvedon artikkelissa Uniform Solution for Uniform Polyhedra.
• Samana vuonna 1993 R. Mäder laati tätä Kaleido-ratkaisua vastaavan ohjelman Mathematica-ohjelmistoon hieman erilaisella indeksointijärjestelmällä.
• Vuonna 2002 Peter W. Messer löysi minimaalisen joukon suljetussa muodossa ilmaistavia lausekkeita, joilla voidaan määrittää minkä tahansa uniformisen monitahokkaan ja sen duaalikappaleen tärkeimmät kombinatoriset ja metriset suureet, kun tunnetaan vain sen Wythoffin symboli.

Kuperat uniformiset monitahokkaat

Wythoffin konstruktiot lähtökohtana suorakulmainen kolmio (p q 2)

Esimerkkinä kuutiosta ja oktaedrista saadut muodot

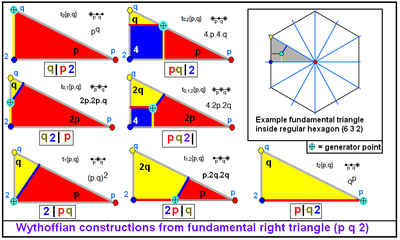
Kuperat uniformiset monitahokkaat voidaan nimetä Wythoffin konstruktio-operaatioilla sen mukaan, mikä on niiden suhde säännöllisiin monitahokkaisiin.

Yksityiskohtaisemmin kuperat uniformiset monitahokkaat luetellaan jäljempänä Wythoffin konstruktioiden mukaan kussakin symmetriaryhmässä.

Wythoffin konstruktio sisältää toistoja, jotka saadaan alemmista symmetrian muodoista. Kuutio on säännöllinen monitahokas ja samalla särmiö, jonka pohjana on neliö. Oktaedri on säännöllinen monitahokas ja samalla antiprisma, jonka tahkot ovat kolmioita. Oktaedri on samalla typistetty tetraedri. Monet monitahokkaat saadaan toistamalla eri konstruktioita, ja sen mukaisesti ne on merkitty eri väreillä.

Wythoffin konstruktio soveltuu yhtä lailla myös uniformisiin monitahokkaisiin sekä pallopinnan uniformisiin tessellaatioihin, minkä vuoksi nekin ovat seuraavissa taulukoissa mukana. Pallopinnan laatoituksiin kuuluvat myös hosoedrit ja diedrit, jotka ovat degeneroituneita monitahokkaita.

Nämä symmetriaryhmät muodostetaan peilauksilla saaduista pisteryhmistä kolmessa ulottuvuudessa, ja kutakin niistä edustaa peruskolmio (p q r), missä p > 1, q > 1, r > 1 ja 1/p + 1/q + 1/r < 1.

• Tetraedrinen symmetria (3 3 2) – kertaluku 24
• Oktaedrinen symmetria (4 3 2) – kertaluku 48
• Ikosaedrinen symmetria (5 3 2) – kertaluku 120
• diedrinen symmetria (n 2 2), missä n = 3,4,5,... – kertaluku 4n

Loput muodot, joilla ei ole peilaussymmetriaa, konstruoidaan alternaatiolla, toisin sanoen poistamalla joka toinen kärki sellaisesta monitahokkaasta, jolla on parillinen määrä tahkoja.

Särmiöiden ja niiden diedrisen symmetrian myötä Wythoffin konstruktioilla pallopinnalla saadaan lisää kaksi säännöllisten tessellaatioiden luokkaa, joita vastaavat monitahokkaat kuitenkin ovat degeneroituneita: diedrit, joilla on vain kaksi tahkoa, ja hosoedrit, joilla on vain kaksi kärkeä. Särmiöt saadaan säännöllisistä hosoedreista typistämällä.

Jäljempänä seuraavissa taulukoissa kuperat uniformiset monitahokkaat, särmiöitä lukuun ottamatta, on merkitty järjestysnumeroilla 1–18, ja ne on lueteltu symmetriaryhmiensä mukaan järjestettyinä.

Prismaattisia muotoja on äärettömän monta, ja ne jakautuvat neljään perheeseen:

1. hosoedrit H_2... (vain pallopinnan tessellaationa)
2. diedrit D_2... (vain pallopinnan tessellaatioina)
3. särmiöt P_3... (typistettyjä hosoedreja)
4. antiprismat A_3... (pullistettujan särmiöitä)

Wythoffin konstruktio-operaatiot

Operaatio	Symboli	Coxeterin diagrammi	Kuvaus
Alkuperäinen	{p,q} t0{p,q}		Mikä tahansa monitahokas tai laatoitus
Suoristettu (r) (engl. rectified)	r{p,q} t1{p,q}	|q	Särmät typistetään täysin niin, että niistä jää jäljelle vain niiden keskipiste. Saadun monitahokkaan tahkoina ovat sekä alkuperäisen monitahokkaan että sen duaalikappaleen tahkojen keskiosat. Monitahokkaat nimetään kahden alkuperäisen monitahokkaan tahkojen lukumäärien mukaan: {p,q} ja {q,p}. Esimerkiksi kuboktaedri r{4,3} saadaan suoristamalla kuutiosta ja oktaedrista.
Kahdesti suoristettu (2r) (engl. birectified) (myös duaali	2r{p,q} t2{p,q}		Kahdesti suoristettu (duaali) saadaan typistämällä edelleen niin, että alkuperäisen monitahokkaan tahkot kutistuvat pisteiksi. Uudet tahkot syntyvät alkuperäisen monitahokkaan jokaisen kärjen ympärille. Särmien lukumäärä on sama kuin alkuperäisessä monitahokkaassa, mutta ne ovat kohtisuorassa alkuperäisen monitahokkaan särmiin nähden. Kahdesti suoritettu monitahokas on sama kuin alkuperäisen monitahokkaan duaalikappale.
Typistetty (t) (engl. truncated)	t{p,q} t0,1{p,q}		Alkuperäisen monitahokkaan jokaisen kärjen ympäriltä leikataan pala pois, ja uusi tahko täyttää syntyneen aukon. Pois leikattavan alueen suuruus voi vaihdella, mutta on vain yksi ratkaisu, jolla saadaan uniforminen typistetty monitahokas. Tämän monitahokkaan tahkoilla on kaksinkertainen määrä sivua alkuperäisen monitahokkaan tahkoihin verrattuna, ja siinä ovat mukana myös duaalikappaleen tahkot.
Kaksoistypistetty (2t) (engl. bitruncated) (myös typistetty duaali)	2t{p,q} t1,2{p,q}	|}}	Kaksoistypistystä voidaan pitää duaalin typistämisenä. Kaksoistypistetty kuutio on typistetty oktaedri.
Kantelloitu (rr)(engl. catellated) (myös laajennettu)	rr{p,q}		Kärkien typistämisen lisäksi jokaista alkuperäistä särmää on leikattu vinoksi niin, että niiden paikalle saadaan uusia suorakulmaisia tahkoja. Uniforminen kantelloitu monitahokas on alkuperäisen monitahokkaan ja sen duaalikappaleen puolivälissä. Kantelloidun monitahokkaan nimi muodostetaan yhdistämällä alkuperäisen monitahokkaan ja sen duaalikappaleen nimet ja lisäämällä näin saadun nimen alkuun etuliike rombi, esimerkiksi kuutiosta ja oktaedrista saadaan rombikuboktaedri rr{4,3}.
Täystypistetty (tr) (engl. Omnitruncated tai cantitruncated)	tr{p,q} t0,1,2{p,q}		Typistys- ja kantellointioperaation yhdistetään. Täystypistetyn monitahokkaan tahkoilla on kaksinkertainen määrä sivuja alkuperäisen monitahokkaan tahkoihin verrattuna, kaksinkertainen määrä tahkoja alkuperäisen kappaleen duaaliin verrattuna ja uusina tahkoina neliöitä alkuperäisen monitahokkaan särmien ympärillä.

Alternaatio-operaatiot

Operaatio	Symboli	Coxeterin diagrammi	Kuvaus
Pullistettu suoritettu (sr) (engl. snub rectified)	sr{p,q}	|	Täystypistetty monitahokas, josta joka toinen kärki on poistettu. Kaikissa alkuperäisissä tahkoissa on vain puolet alkuperäisten sivujen lukumääristä, ja neliöt surkastuvat särmiksi. Koska täystypistetyissä muodoissa on kolme tahkoa kärkeä kohti, muodostuu uusia kolmioita. Yleensä nämä alternoivat tahkojen muodot poikkeavat jonkin verran alkuperäisistä, jotta saadaan jälleen uniformiset monitahokkaat. Jälkimmäisen variaation mahdollisuus riippuu vapausasteesta.
Pullistettu (s) (engl. snub)	s{p,2q}		Alternoitu typistetty
kanttinen pullistettu (s2) engl. cantic snub)	s2{p,2q}
Alternoidusti kantelloitu (hrr) engl. Alternated cantellation)	hrr{2p,2q}	}}	Mahdollinen vain uniformisille tessellaatioille, jotka voidaan käsittää äärettömiksi monitahokkaiksi. Saadaan alternaatiolla operaatiosta Esimerkiksi
Puoli (h)	h{2p,q}		Saadaan alternaatiolla operaatiosta , sama kuin Tiedosto:CDel labelp
Kanttinen (h2) (engl. cantic)	h2{2p,q}		Sama kuin
Puolisuoristettu (hr) (engl. half rectified)	hr{2p,2q}		Mahdollinen vain uniformisille tessellaatioille. Saadaan alternaatiolla operaatiosta , sama kuin tai Esimerkiksi = tai
Neljännes (q)	q{2p,2q}		Mahdollinen vain uniformisille tessellaatioille, sama kuin Esimerkiksi }} = tai

Taulukot monitahokkaista johdettuina säännöllisistä monitahokkaista

	Alkuperäinen	Typistetty	Suoristettu	Kaksoistypistetty (typ. duaali)	Kaksoissuoristettu (duaali)	Kantelloitu	Täystypistetty	Pullistettu
Coxeterin diagrammi
Laajennettu Schläflin symboli	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	ht0,1,2{p,q}
Wythoffin symboli (p q 2)	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Kärkikonfiguraatio	pq	q.2p.2p	(p.q)2	p.2q.2q	qp	p.4.q.4	4.2p.2q	3.3.p.3.q
Tetraedrinen (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Oktaedrinen (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Ikosaedrinen (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

Seuraavassa taulukossa ovat pallopinnan tessellaatiot, joilla on diedrinen symmetria:

(p 2 2)	Alkuperäinen	Typistetty	Suoristettu	Kaksoistypistetty (typ. duaali)	Kaksoissuoristettu (duaali)	Kantelloitu	Täystypistetty	Pullistettu
Coxeterin diagrammi
Laajennettu Schläflin symboli	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	${\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{p,2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t0{p,2}	t0,1{p,2}	t1{p,2}	t1,2{p,2}	t2{p,2}	t0,2{p,2}	t0,1,2{p,2}	ht0,1,2{p,2}
Wythoffin symboli	2 | p 2	2 2 | p	2 | p 2	2 p | 2	p | 2 2	p 2 | 2	p 2 2 |	| p 2 2
Kärkikonfiguraatio	p2	2.2p.2p	p.2.p.2	p.4.4	2p	p.4.2.4	4.2p.4	3.3.3.p
Diedrinen (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Diedrinen (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	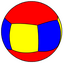4.4.6	3.3.3.3
Diedrinen (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
Diedrinen (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	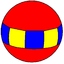4.4.10	3.3.3.5
Diedrinen (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

Tetraedrisesti symmetriset monitahokkaat

Pallopinnan tetraedrisella symmetrialla (T_d saadaan viisi uniformista monitahokasta, ja kuudes saadaan pullistusoperaatiolla.

Tetraedrinen symmetria saadaan lähtemällä peruskolmiosta, jonka yhdessä kärjessä on kaksi peiliä, molemmissa muissa kaksi peiliä, ja sitä esittää symboli (3 3 2). Sitä esittää myös Coxeterin ryhmä A₂ tai [3,3], taikka Coxeterin diagrammi: .

Näin saadaan 24 kolmiota, jotka muodostavat seuraavan tetrakis-heksaedrin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Graafi A3	Graafi A2	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
								Pos. 2 [3] (4)	Pos. 2 [2] (6)	Pos. 2 [3] (4)	Tahkoja	Särmiä	Kärkiä
1	Tetraedri						{3,3}	{3}			4	6	4
[1]	Kahdesti suoristettu tetraedri (Sama kuin tetraedri)						t2{3,3}={3,3}			{3}	4	6	4
2	Suoristettu tetraedri (Sama kuin oktaedri)						t1{3,3}=r{3,3}	{3}		{3}	8	12	6
3	Typistetty tetraedri						t0,1{3,3}=t{3,3}	{6}		{3}	8	18	12
[3]	Kaksoistypistetty tetraedri (Sama kuin typistetty tetraedri)						t1,2{3,3}=t{3,3}	{3}		{6}	8	18	12
4	Rombitetratetraedri (Sama kuin kuboktaedri)						t0,2{3,3}=rr{3,3}	{3}	{4}	{3}	14	24	12
5	Typistetty tetratetraedri (Sama kuin typistetty oktaedri)						t0,1,2{3,3}=tr{3,3}	{6}	{4}	{6}	14	36	24
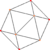
6	Pullistettu tetratetraedri (Sama kuin ikosaedri)						sr{3,3}	{3}	2 {3}	{3}	20	30	12

Oktaedrisesti symmetriset monitahokkaat

Pallopinnan oktaedrisella symmetrialla (O_h) saadaan seitsemän uniformista monitahokasta, ja toiset seitsemän saadaan poistamalla näin saaduista joka toinen kärki. Näistä 14 muodosta kuusi on samoja, jotka esiintyvät myös edellä tetraedristesti symmetristen monitahokkaiden taulukossa.

Oktaedrinen symmetria saadaan lähtemällä peruskolmiosta (4 3 2), jossa nämä luvut tarkoittavat peilien lukumääriä sen kussakin kärjessä. Sitä esittää myös Coxeterin ryhmä B₂ tai [4,3], taikka Coxeterin diagrammi: .

Näin saadaan 48 kolmiota, jotka muodostavat seuraavan disdyakis-dodekaedrin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Graafi B3	Graafi B2	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
								Pos. 2 [4] (6)	Pos. 1 6px	Pos. 0 [3] (8)	Tahkoja	Särmiä	Kärkiä
7	Kuutio						{4,3}	{4}			6	12	8
[2]	Oktaedri						{3,4}			{3}	8	12	6
[4]	Suoristettu kuutio Suoristettu oktaedri (Kuboktaedri)						{4,3}	{4}		{3}	14	24	12
8	Typistetty kuutio						t0,1{4,3}=t{4,3}	{8}		{3}	14	36	24
[5]	Typistetty oktaedri						t0,1{3,4}=t{3,4}	{4}		{6}	14	36	24
9	Kantelloitu kuutio Kantelloitu oktaedri rombikuboktaedri						t0,2{4,3}=rr{4,3}	{8}	{4}	{6}	26	48	24
10	Täystypistetty kuutio täystypistetty oktaedri typistetty kuboktaedri						t0,1,2{4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	Pullistettu oktaedri (Sama kuin ikosaedri)						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	Puolikuutio (Sama kuin tetraedri)						= h{4,3}={3,3}	1/2 {3}			4	6	4
[2]	Kanttinen kuutio (Sama kuin typistetty tetraedri)						= h2{4,3}=t{3,3}	1/2 {6}		1/2 {3}	8	18	12
[4]	(Sama kuin kuboktaedri)						= rr{3,3}				14	24	12
[5]	(Sama kuin typistetty oktaedri)						|}} = tr{3,3}				14	36	24
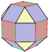
[9]	Kanttinen pullistettu oktaedri (sama kuin rombikuboktaedri)						s2{3,4}=rr{3,4}				26	48	24
11	Pullistettu kuutio Pullistettu kuboktaedri						sr{4,3}	{4}	2 {3}	{3}	38	60	24

Ikosaedrisesti symmetriset monitahokkaat

Pallopinnan ikosaedrisella symmetrialla (I_h) saadaan seitsemän uniformista monitahokasta sekä vielä yksi lisää poistamalla joka toinen kärki. Näin saaduista kahdeksasta muodosta vain yksi on sama, joka esiintyy myös edellä tetraedrisesti ja oktaedristen monitahokkaiden taulukoissa.

Oktaedrinen symmetria saadaan lähtemällä peruskolmiosta (5 3 2), jossa nämä luvut tarkoittavat peilien lukumääriä sen kussakin kärjessä. Sitä esittää myös Coxeterin ryhmä G₂ tai [4,3], taikka Coxeterin diagrammi: .

Näin saadaan 120 kolmiota, jotka muodostavat seuraavan disdyakis-triakontaedrin tahkot ja jotka seuraavassa esitetään vuorottelevin värein pallon pinnalla:

#	Nimi	Graafi A3	Graafi A2	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
								Pos. 2 [5] (12)	Pos. 1 [2] (30)	Pos. 0 [3] (20)	Tahkoja	Särmiä	Kärkiä
12	Dodekaedri						{5,3}	{5}			12	30	20
[6]	Ikosaedri						}} {3,5}			{3}	20	30	12
13	Suoritettu dodekaedri Suoristettu ikosaedri Ikosidodekaedri						t1{5,3}=r{5,3}	{5}		{3}	32	60	30
14	Typistetty dodekaedri						|3 t0,1{5,3}=t{5,3}	{10}		{3}	32	90	60
15	Typistetty ikosaedri		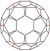				}} t0,1{3,5}=t{3,5}	{5}		{6}	32	90	60
16	Kantelloitu dodekaedri Kantelloitu ikosaedri Rombikosidodekaedri						}} t0,2{5,3}=rr{5,3}	{5}	{4}	{3}	62	120	60
17	Täystypistetty dodekaedri Täystypistetty ikosaedri Typistetty ikosidodekaedri						}} t0,1,2{5,3}=tr{5,3}	{10}	[4}	{6}	62	180	120
18	Pullistettu dodekaedri Pullistettu ikosidodekaedri						sr{5,3}	{5}	2 {3}	{3}	92	150	60

Diedrinen symmetria, särmiöt ja antiprismat

Pallopinnan diedrisella symmetrialla (D_ph) saadaan kaksi ääretöntä joukkoa uniformisia monitahokkaita, särmiöt ja antiprismat, sekä lisäksi kaksi ääretöntä joukkoa degeneroituja monitahokkaita, hosoedrit ja dihedrit, joita vastaavat tietyt laatoitukset eli tessellaatiot pallon pinnalla.

Diedrinen symmetria saadaan lähtemällä peruskolmiosta (p 2 2), jossa nämä luvut tarkoittavat peilien lukumääriä sen kussakin kärjessä. Sitä esittää myös Coxeterin ryhmä I₂(p) tai [n2], taikka Coxeterin diagrammi: .

Seuraavassa esitetään viisi ensimmäistä diedristä symmetriaa: D₂ ... D₆. Diedrinen symmetria D_p on kertalukua 4n ja esittää bipyramidin tahkoja. Pallopinnalla sitä vastaa päiväntasaaja pituussuunnassa sekä tasavälein n pituuspiiriä.

Diedrinen symmetria (2 2 2)

Diedrisellä symmetrialla D_2h (2 2 2) saadaan 8 peruskolmiota, jotka muodostavat seuraavassa näkyvän neliöpohjaisen bipyramidin eli oktaedrin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
						Pos. 2 | [2] (2)	Pos. 1 [2] (2)	Pos. 0 [2] (2)	Tahkoja	Särmiä	Kärkiä
D2 H2	kaksikulmainen diedri kaksikulmainen hosoedri				{2,2}	{2}			2	2	2
D4	Typistetty kaksikulmainen diedri (Sama kuin neliödiedri)				t{2,2}={4,2}	[4}			2	4	4
P4 [7]	Täystypistetty kaksikulmainen diedri (Sama kuin kuutio)				}} t0,1,2{2,2}=tr{2,2}	{4}	{4}	[4}	6	12	8
A2 [1]	Pullistettu kaksikulmainen diedri sama kuin tetraedri)				sr{2,2}		2 {3}		4	6	4

Diedrinen symmetria (3 2 2)

Diedrisellä symmetrialla D_3h (3 2 2) saadaan 12 peruskolmiota, jotka muodostavat seuraavan kuusikulmaisen bipyramidin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
						Pos. 2 [3] (2)	Pos. 1 [2] (3)	Pos. 0 [2] (3)	Tahkoja	Särmiä	Kärkiä
D3	Kolmikulmainen diedri				{3,2}	{3}			2	3	3
H3	Kolmikulmainen hosoedri				{2,3}			{2}	3	3	2
D6	Typistetty kolmikulmainen diedri (sama kuin kuusikulmainen diedri)				t{3,2}	{6}			2	6	6
P3	Typistetty kolmikulmainen hosoedri (Kolmikulmainen särmiö)				t{2,3}	{3}	[4}		5	9	6
P6	Täystypistetty kolmikulmainen diedri (Kuusikulmainen särmiö)				Tiedosto:CDel 3.pnx}} t0,1,2{2,3}=tr{2,3}	{6}	[4}	[4}	8	18	12
A3 [2]	Pullistettu kolmikulmainen diedri (Sama kuin kolmikulmainen antiprisma) (Sama kuin oktaedri)				sr{2,3}	{3}	2 {3}		8	12	6
P3	Kanttinen pullistettu kolmikulmainen diedri (Kolmikulmainen särmiö)				}} s2{2,3}=t{2,3}				5	9	6

Diedrinen symmetria (4 2 2)

Diedrisellä symmetrialla D_4h (4 2 2) saadaan 12 peruskolmiota, jotka muodostavat seuraavan kahdeksankulmaisen bipyramidin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
						Pos. 2 [4] (2)	Pos. 1 [2] (4)	Pos. 0 [2] (4)	Tahkoja	Särmiä	Kärkiä
D4	neliödiedri				{4,2}	[4}			2	4	4
H4	neliöhosoedri				{2,4}			{2}	4	4	2
D8	Typistetty neliödiedri (Sama kuin kahdeksankulmainen diedri)				|2 t{4,2}	{8}			2	8	8
P4 [7]	Typistetty neliöhosoedri (Kuutio)				}} t{2,4}	{4}	{4}		6	12	8
D8	Täystypistetty neliödiedri (Kahdeksankulmainen särmiö)				|2 t0,1,2{2,4}=tr{2,4}	{8}	[4}	[4}	10	24	16
A4	Pullistettu neliödiedri (Neliöpohjainen antiprisma)				Tiedosto:CDel node hTiedosto:CDel node hTiedosto:CDel node h sr{2,4}	[4}	2 {3}		10	16	8
P4 [7]	Kanttinen pullistettu neliödiedri (Kuutio)				Tiedosto:CDel node hTiedosto:CDel node h s2{4,2}=t{2,4}				6	12	8
A2 [1]	Pullistettu neliöpohjainen hosoedri (Kaksikulmainen hosoedri) (Tetraedri)				Tiedosto:CDel node hTiedosto:CDel node h s{2,4}=sr{2,2}				4	6	4

Diedrinen symmetria (5 2 2)

Diedrisellä symmetrialla D_5h (4 2 2) saadaan 20 peruskolmiota, jotka muodostavat seuraavan kymmenkulmaisen bipyramidin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
						Pos. 2 [5] (2)	Pos. 1 [2] (5)	Pos. 0 [2] (5)	Tahkoja	Särmiä	Kärkiä
D5	Viisikulmainen diedri				{5,2}	{5}			2	5	5
H5	Viisikulmainen hosoedri				{2,5}			{2}	5	5	2
D10	Typistetty viisikulmainen diedri (Sama kuin kymmenkulmainen diedri)				t{5,2}	{10}			2	10	10
P5	Typistetty viisikulmainen hosoedri (Sama kuin viisikulmainen särmiö)				t{2,5}	{5}	[4}		7	15	10
P10	Täystypistetty viisikulmainen diedri (Kymmenkulmainen särmiö)				t0,1,2{2,5}=tr{2,5}	{10}	[4}	[4}	12	30	20
A5	Pullistettu viisikulmainen diedri (Viisikulmainen antiprisma)				Tiedosto:CDel node hTiedosto:CDel node hTiedosto:CDel node h}} sr{2,5}	{5}	2 {3}		12	20	10
P5	Kanttinen pullistettu viisikulmainen diedri (Viisikulmainen särmiö)				Tiedosto:CDel node hTiedosto:CDel node h s2{5,2}=t{2,5}				7	15	10

Diedrinen symmetria (6 2 2)

Diedrisellä symmetrialla D_6h (4 2 2) saadaan 24 peruskolmiota, jotka muodostavat seuraavan kaksitoistakulmaisen bipyramidin tahkot ja jotka seuraavassa esitetään myös vuorottelevin värein pallon pinnalla:

#	Nimi	Kuva	Laatoitus	Kärkikuvio	Coxeterin ja Schläflin symbolit	Tahkojen muodot eri positioissa			Elementtien lukumäärät
						Pos. 2 [6] (2)	Pos. 1 [2] (6)	Pos. 0 [2] (6)	Tahkoja	Särmiä	Kärkiä
D6	Kuusikulmainen diedri				{6,2}	{6}			2	6	6
H6	Kuusikulmainen hosoedri				{2,6}			{2}	6	6	2
D12	Typistetty kuusikulmainen diedri (Sama kuin kaksitoistakulmainen diedri)				|2 t{6,2}	{12}			2	12	12
H6	Typistetty kuusikulmainen hosoedri (Sama kuin kuusikulmainen särmiö)				}} t{2,6}	{6}	[4}		8	18	12
P12	Täystypistetty kuusikulmainen diedri (12-kulmainen särmiö)				|2}} t0,1,2{2,6}=tr{2,6}	{12}	[4}	[4}	14	36	24
A6	Pullistettu kuusikulmainen diedri (Kuusikulmainen antiprisma)				Tiedosto:CDel node hTiedosto:CDel node hTiedosto:CDel node h sr{2,6}	{6}	2 {3}		14	24	12
P3	Kanttinen kuusikulmainen diedri (Kolmikulmainen särmiö)				= h2{6,2}=t{2,3}				5	9	6
P6	Kanttinen pullistettu kuusikulmainen diedri (Kuusikulmainen särmiö)				Tiedosto:CDel node hTiedosto:CDel node h}} s2{6,2}=t{2,6}				8	18	12
A3 [2]	Pullistettu heksagonaalinen hosoedri (Sama kuin triangulaarinen antiprisma) (Sama kuin oktaedri)				Tiedosto:CDel node hTiedosto:CDel node h}} s{2,6}=sr{2,3}				8	12	6

Uniformiset tähtimonikulmiot

Uniformisia tähtimonitahokkaita, jotka eivät ole särmiöitä, on kaikkiaan 57. Ne voidaan muodostaa Wythoffin konstruktiolla Schwarzin kolmioista.

Uniformisista tähtimonitahokkaista neljä on säännöllisiä (Kepler-Poinsotin kappaleet), viisi kvasisäännöllistä ja loput 48 semiregulaarisia.

Eri tutkijat ovat numeroineet uniformiset monitahokkaat eri tavoin. Seuraavissa taulukoissa sarake C# tarkoittaa Coxeterin vuonna 1954, W# Wenningerin vuonna 1974 ja K# Kaleidon vuonna 1993 käyttämää numerointia. Coxeterin numeroinnissa kuperat muodot saivat numerot 15–32, kolme prismaattista muotoa numerot 33–35 ja ei-kuperat muodot numerot 36–92. Wenninger antoi Platonin kappaleille numerot 1–5, Arkhimedeen kappaleille numerot 6–18, tähtimäisille muodoille numerot 19–66, mihin sisältyy myös neljä säännöllistä ei-kuperaa monitahokasta, sekä loput numerot 67–119 ei-kuperille uniformisille monitahokkaille. Kaleidon numeroinnissa 80 muotoa ryhmiteltiin symmetrian mukaan: numerot 1–4 kuuluivat sellaisten prismaattisten muotojen äärettömille perheille, joilla on diedrinen symmetria, numerot 6–9 tetraedrisesti, numerot 10–26 oktaedrisesti ja numerot 46–80 ikosaedrisesti symmetrisille kappaleille. U# tarkoittaa Mathematica -teoksessa käytettyä numerointia, joka eroaa Kaleidon numeroinnista siinä, että viisi prismaattista muotoa siirrettiin viimeisiksi, jolloin ei-prismaattiset muodot saivat numerot 1–75. Sarake ”Khii” taulukoissa tarkoittaa Eulerin karakteristikaa.

Särmiöt eivät ole mukana seuraavissa taulukoissa.

Kepler–Poinsotin kappaleet

Nimi	Kuva	Wythoffin symboli	Kärki- kuvio	Symm.	C#	W#	U#	K#	Kärkiä	Särmiä	Tahkoja	Khii	Orien- toituva?	Tiheys	Tahkojen tyypit
Suuri dodekaedri		5/2 | 2 5	(5.5.5.5.5)/2	Ih	C44	W021	U35	K40	12	30	12	-6	Kyllä	3	12{5}
Suuri ikosaedri		5/2 | 2 3	(3.3.3.3.3)/2	Ih	C69	W041	U53	K58	12	30	20	2	Kyllä	7	20{3}
Pieni tähti- dodekaedri		5 | 2 5/2	(5/2)5	Ih	C43	W020	U34	K39	12	30	12	-6	Kyllä	3	12{5/2}
Suuri tähti- dodekaedri		3 | 2 5/2	(5/2)3	Ih	C68	W022	U52	K57	20	30	12	2	Kyllä	7	12{5/2}

Kvasisäännölliset uniformiset tähtimonitahokkaat

Nimi	Kuva	Wythoffin symboli	Kärki- kuvio	Symm.	C#	W#	U#	K#	Kärkiä	Särmiä	Tahkoja	Khii	Orien- toituva?	Tiheys	Tahkojen tyypit
Suuri ikosidodekaedri		2 | 5/2 3	(5/2.3)2	Ih	C70	W094	U54	K59	30	60	32	2	Kyllä	7	20{3}+12{5/2}
Dodeka- dodekaedri		2 | 5/2 5	(5/2.5)2	Ih	C45	W073	U36	K41	30	60	24	-6	Kyllä	3	12{5}+12{5/2}
Pieni trigonaarinen ikosidodekaedri		3 | 5/2 3	(5/2.3)3	Ih	C39	W070	U30	K35	20	60	32	-8	Kyllä	2	20{3}+12{5/2}
Ditrigonaalinen dodekadodekaedri		3 | 5/3 5	(5/3.5)3	Ih	C53	W080	U41	K46	20	60	24	-16	Kyllä	4	12{5}+12{5/2}
Suuri ditrigonaalinen ikosidodekaedri		3/2 | 3 5	(5.3.5.3.5.3)/2	Ih	C61	W087	U47	K52	20	60	32	-8	Kyllä	6	20{3}+12{5}

|}

Muut uniformiset tähtimonitahokkaat

Nimi	Kuva	Wythoffin symboli	Kärki- kuvio	Symm.	C#	W#	U#	K#	Kärkiä	Särmiä	Tahkoja	Khii	Orien- toituva?	Tiheys	Tahkojen tyypit
Oktahemioktaedri		3/2 3 | 3	6.3/2.6.3	Oh	C37	W068	U03	K08	12	24	12	0	Kyllä		8{3}+4{6}
Tetrahemiheksaedri		3/2 3 | 2	4.3/2.4.3	Td	C36	W067	U04	K09	6	12	7	1	Ei		4{3}+3{4}
Kubohemioktaedri		4/3 4 | 3	6.4/3.6.4	Oh	C51	W078	U15	K20	12	24	10	-2	Ei		6{4}+4{6}
Pieni rombiheksaedri		2 4 (3/2 4/2) |	4.8.4/3.8/7	Oh	C60	W086	U18	K23	24	48	18	-6	Ei		12{4}+6{8}
Pieni kubikuboktaedri		3/2 4 | 4	8.3/2.8.4	Oh	C38	W069	U13	K18	24	48	20	-4	Kyllä	2	8{3}+6{4}+6{8}
Ei-kupera suuri rombikuboktaedri		3/2 4 | 2	4.3/2.4.4	Oh	C59	W085	U17	K22	24	48	26	2	Kyllä	5	8{3}+(6+12){4}
Pieni dodekahemi- dodekaedri		5/4 5 | 5	10.5/4.10.5	Ih	C65	W091	U51	K56	30	60	18	-12	Ei		12{5}+6{10}
Suuri dodekahemi- ikosaedri		5/4 5 | 3	6.5/4.6.5	Ih	C81	W102	U65	K70	30	60	22	-8	Ei		12{5}+10{6}
Pieni ikosihemi- dodekaedri		3/2 3 | 5	10.3/2.10.3	Ih	C63	W089	U49	K54	30	60	26	-4	Ei		20{3}+6{10}
Pieni dodekikosaedri		3 5 (3/2 5/4) |	10.6.10/9.6/5	Ih	C64	W090	U50	K55	60	120	32	-28	Ei		20{6}+12{10}
Pieni rombidodekaedri		2 5 (3/2 5/2) |	10.4.10/9.4/3	Ih	C46	W074	U39	K44	60	120	42	-18	Ei		30{4}+12{10}
Pieni dodekikosi- dodekaedri		3/2 5 | 5	10.3/2.10.5	Ih	C42	W072	U33	K38	60	120	44	-16	Kyllä	2	20{3}+12{5}+12{10}
Rombikoksaedri		2 3 (5/4 5/2) |	6.4.6/5.4/3	Ih	C72	W096	U56	K61	60	120	50	-10	Ei		30{4}+20{6}
Suuri ikosikosi- dodekaedri		3/2 5 | 3	6.3/2.6.5	Ih	C62	W088	U48	K53	60	120	52	-8	Kyllä	6	20{3}+12{5}+20{6}
Tähtimäinen typistetty heksaedri		2 3 | 4/3	8/3.8/3.3	Oh	C66	W092	U19	K24	24	36	14	2	Kyllä	7	8{3}+6{8/3}
Suuri rombiheksaedri		2 4/3 (3/2 4/2) |	4.8/3.4/3.8/5	Oh	C82	W103	U21	K26	24	48	18	-6	Ei		12{4}+6{8/3}
Suuri kubikuboktaedri		3 4 | 4/3	8/3.3.8/3.4	Oh	C50	W077	U14	K19	24	48	20	-4	Kyllä	4	8{3}+6{4}+6{8/3}
Suuri dodekahemi- dodekaedri		5/35/2 | 5/3	10/3.5/3.10/3.5/2	Ih	C86	W107	U70	K75	30	60	18	-12	Ei		12{5/2}+6{10/3}
Pieni dodekahemi- ikosaedri		5/35/2 | 3	6.5/3.6.5/2	Ih	C78	W100	U62	K67	30	60	22	-8	Ei		12{5/2}+10{6}
Suuri ikosihemi- dodekaedri		3/2 3 | 5/3	10/3.3/2.10/3.3	Ih	C85	W106	U71	K76	30	60	26	-4	Ei		20{3}+6{10/3}
Kubitypistetty kuboktaedri		4/3 3 4 |	8/3.6.8	Oh	C52	W079	U16	K21	48	72	20	-4	Kyllä	4	8{6}+6{8}+6{8/3}
Suuri typistetty kuboktaedri		4/3 2 3 |	8/3.4.6/5	Oh	C67	W093	U20	K25	48	72	26	2	Kyllä	1	12{4}+8{6}+6{8/3}
Typistetty suuri dodekaedri		2 5/2 | 5	10.10.5/2	Ih	C47	W075	U37	K42	60	90	24	-6	Kyllä	3	12{5/2}+12{10}
Pieni tähtimäinen typistetty dodekaedri		2 5 | 5/3	10/3.10/3.5	Ih	C74	W097	U58	K63	60	90	24	-6	Kyllä	9	12{5}+12{10/3}
Suuri tähtimäinen typistetty dodekaedri		2 3 | 5/3	10/3.10/3.3	Ih	C83	W104	U66	K71	60	90	32	2	Kyllä	13	20{3}+12{10/3}
Typistetty suuri ikosaedri		2 5/2 | 3	6.6.5/2	Ih	C71	W095	U55	K60	60	90	32	2	Kyllä	7	12{5/2}+20{6}
Suuri dodekikosaedri		3 5/3(3/2 5/2) |	6.10/3.6/5.10/7	Ih	C79	W101	U63	K68	60	120	32	-28	Ei		20{6}+12{10/3}
Suuri rombidodekaedri		2 5/3 (3/2 5/4) |	4.10/3.4/3.10/7	Ih	C89	W109	U73	K78	60	120	42	-18	Ei		30{4}+12{10/3}
Ikosidodeka- dodekaedri		5/3 5 | 3	6.5/3.6.5	Ih	C56	W083	U44	K49	60	120	44	-16	Kyllä	4	12{5}+12{5/2}+20{6}
Pieni trigonaalinen dodekikosi- dodekaedri		5/3 3 | 5	10.5/3.10.3	Ih	C55	W082	U43	K48	60	120	44	-16	Kyllä	4	20{3}+12{;5/2}+12{10}
Suuri trigonaalinen dokekikosi- dodekaedri		3 5 | 5/3	10/3.3.10/3.5	Ih	C54	W081	U42	K47	60	120	44	-16	Kyllä	4	20{3}+12{5}+12{10/3}
Suuri dodekikosi- dodekaedri		5/2 3 | 5/3	10/3.5/2.10/3.3	Ih	C77	W099	U61	K66	60	120	44	-16	Kyllä	10	20{3}+12{5/2}+12{10/3}
Pieni ikosikosi- dodekaedri		5/2 3 | 3	6.5/2.6.3	Ih	C40	W071	U31	K36	60	120	52	-8	Kyllä	2	20{3}+12{5/2}+20{6}
Rombodideka- dodekaedri		5/2 5 | 2	4.5/2.4.5	Ih	C48	W076	U38	K43	60	120	54	-6	Kyllä	3	30{4}+12{5}+12{5/2}
Suuri rombikosi- dodekaedri		5/3 3 | 2	4.5/3.4.3	Ih	C84	W105	U67	K72	60	120	62	2	Kyllä	13	20{3}+30{4}+12{5/2}
Ikositypistetty dodeka- dodekaedri		5/3 3 5 |	10/3.6.10	Ih	C57	W084	U45	K50	120	180	44	-16	Kyllä	4	20{6}+12{10}+12{10/3}
Typistetty dodeka- dodekaedri		5/3 2 5 |	10/3.4.10/9	Ih	C75	W098	U59	K64	120	180	54	-6	Kyllä	3	30{4}+12{10}+12{10/3}
Suuri typistetty ikosidodekaedri		5/3 2 3 |	10/3.4.6	Ih	C87	W108	U68	K73	120	180	62	2	Kyllä	13	30{4}+20{6}+12{10/3}
Pullistettu dodeka- dodekaedri		| 2 5/2 5	3.3.5/2.3.5	I	C49	W111	U40	K45	60	150	84	-6	Kyllä	3	60{3}+12{5}+12{5/2}
Invertoitu pullistettu dodeka- dodekaedri		| 5/3 2 5	3.5/3.3.3.5	I	C76	W114	U60	K65	60	150	84	-6	Kyllä	9	60{3}+12{5}+12{5/2}
Suuri pullistettu ikosidodekaedri		| 2 5/2 3	34.5/2	I	C73	W116	U57	K62	60	150	92	2	Kyllä	7	(20+60){3}+12{5/2}
Suuri invertoitu pullistettu ikosidodekaedri		| 5/3 2 3	34.5/3	I	C88	W113	U69	K74	60	150	92	2	Kyllä	13	(20+60){3}+12{5/2}
Suuri retropullistettu ikosidodekaedri		| 3/25/3 2	(34.5/2)/2	I	C90	W117	U74	K79	60	150	92	2	Kyllä	37	(20+60){3}+12{5/2}
Suuri pullistettu dodekikosi- dodekaedri		| 5/35/2 3	33.5/3.3.5/2	I	C80	W115	U64	K69	60	180	104	-16	Kyllä	10	(20+60){3}+(12+12){5/2}
Pullistettu ikosidodeka- dodekaedri		| 5/3 3 5	33.5.5/3	I	C58	W112	U46	K51	60	180	104	-16	Kyllä	4	(20+60){3}+12{5}+12{5/2}
Pieni pullistettu ikosikosi- dodekaedri		| 5/2 3 3	35.5/2	Ih	C41	W110	U32	K37	60	180	112	-8	Kyllä	2	(40+60){3}+12{5/2}
Pieni retropullistettu ikosikosi- dodekaedri		| 3/23/25/2	(35.5/3)/2	Ih	C91	W118	U72	K77	60	180	112	-8	Kyllä	38	(40+60){3}+12{5/2}
Suuri dirombikokosi- dodekaedri		| 3/25/3 3 5/2	(4.5/3.4.3. 4.5/2.4.3/2)/2	Ih	C92	W119	U75	K80	60	240	124	-56	Ei		40{3}+60{4}+24{5/2}

Luetteloon voidaan lisätä vielä seuraava suuri kaksoispullistettu dirombododekaedri, jonka 360 särmästä 240 on pareittain päällekkäin muodostaen 120 kahden yhtyvän särmän paria. Koska sen särmät ovat tällä tavoin degeneroituneet, sitä ei aina lueta uniformisiin monitahokkaisiin kuuluvaksi. Jos nämä 120 paria lasketaan kukin yhdeksi särmäksi, jossa toisensa kohtaa neljä tahkoa, kappaleella on vain 240 särmää, ja sen Eulerin karakteristikaksi saadaan 24.

Nimi	Kuva	Wythoffin symboli	Kärki- kuvio	Symm.	C#	W#	U#	K#	Kärkiä	Särmiä	Tahkoja	Khii	Orien- toituva?	Tiheys	Tahkojen tyypit
Suuri kaksoispullistettu dirombidodekaedri		| (3/2) 5/3 (3) 5/2	(5/2.4.3.3.3.4. 5/3. 4.3/2.3/2.3/2.4)/2	Ih	--	--	--	--	60	360 (*)	204	-96	Ei		120{3}+60{4}+24{5/2}

Lähteet

• M. Brückner: Vielecke und vielflache. Theorie und geschichte. Leipzig: Teubner, 1900. Teoksen verkkoversio.
• Magnus Wenninger: Polyhedron Models. Cambridge University Press, 1974. ISBN 0-521-09859-9
• J. Skilling: The complete set of uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 6.3.1975, 278. vsk, nro 1278, s. 111–135. doi:10.1098/rsta.1975.0022 ISSN 0080-4614
• UniformPolyhedron.html Wolfram MathWorld. Eric W. Weisstein. Viitattu 20.11.2018.

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Uniforminen monitahokas Wikimedia Commonsissa