Ikosidodekaedri

Ikosidodekaedri on monitahokas, jolla on sivutahkoinaan 20 tasasivuista kolmiota ja 12 säännöllistä viisikulmiota Sillä on 30 keskenään samanlaista kärkeä, joista jokaisessa kohtaa toisensa kaksi kolmiota ja kaksi viisikulmiota, sekä 60 keskenään samanlaista särmää, joista jokaisen toisella puolella on kolmio, toisella puolella viisikulmio. Ikosidodekaedri kuuluu Arkhimedeen kappaleisiin ja on myös kvasisäännöllinen monitahokas.

Nimi ikosidodekaedri johtuu kreikan kielen lukusanoista ikosi, είκοσι (20) ja dodeka, δώδεκα (12) ja viittaa siten kappaleen eri muotoisten sivutahkojen lukumääriin.

Geometria

Ikosidodeakaedrilla on ikosaedrinen symmetria, ja sen ensimmäinen stellaatio on sellaisen dodekaedrin ja sen duaalikappaleen ikosaedrin yhdistelmä, joiden sivujen keskipisteissä ikosidodekaedrin kärjet ovat.

Ikosaedrin duaalikappale on rombinen triakontaedri. Ikosidodekaedrin läpi kulkee kuusi sellaista tasoa, joista jokaisella se voidaan jakaa kahdeksi pentagonaaliseksi rotundaksi, jotka kuuluvat Johnsonin kappaleisiin.

Ikosikodekaedri voidaan käsittää pentagonaaliseksi gyrobirotunda, kahden pentagonaalinen rotundan yhdistelmäksi. Yhdistämällä nämä rotundat eri tavalla voidaan muodostaa myös pentagonaalinen ortobirotunda, joka on yksi Johnsonin kappaleista. Tässä muodossa sillä on diedrinen symmetria D_5d, [10,2⁺], (2*5), kertalukua 20.

Ikosidodekaedrin särmät voidaan kuvata perspektiivisesti kuudella kymmenkulmiolla, joista kaksi leikkaa toisensa jokaisessa kappaleen 30 kärkipisteestä.

Ikosidodekaedrin keskipisteen kautta kulkee kuusi sellaista tasoa, että kun jokin niistä leikataan ikosidodekaedrin kanssa, leikkauskuviona saadaan säännöllinen kymmenkulmio. Jos nämä kymmenkulmiot projisoidaan pallopinnalle, ne muodostavat siinä kuusi isoympyrää. Buckminster Fuller käytti näitä kuutta isoympyrää sekä kahdesta muusta monitahokkaasta saatavaa isoympyrää, joista toisesta niitä saatiin 15, toisesta 10, määritellessään palloikosaedrin 31 isoympyrää.

Ikosidodekaedrin Schläflin symboli on {3 5}.

Karteesiset koordinaatit

Jos ikosaedrin keskipiste on origossa ja sen särmä on yhden pituusyksikön pituinen, sen kärkien karteesiset koordaatit voivat olla esimerkiksi:

• $(0,0,\pm \phi )$
• $(\pm {\frac {1}{2}},\pm {\frac {\phi }{2}},\pm {\frac {\phi ^{2}}{2}})$

sekä näiden kaikki parilliset permutaatiot, missä $\phi$ on kultainen suhde, ${\frac {1}{2}}+{\frac {\sqrt {5}}{2}}$.

Ortogonaaliset projektiot

Ikosidodekaedrilla on neljä erityistä ortogonaalista projektiota, joiden keskuksina ovat kärki, särmä, kolmiomainen sivu ja viisikulmainen tahko. Kaksi jälkimmäistä vastaavat Coxeterin tasoja A₂ ja H₂

Ortogonaalinen projektio

Keskuksena	Kärki	Särmä	Kolmiomainen tahko	Viisikulmainen tahko
Kappale
Särmien muodostama kuvio
Projektiivinen symmetria	[2]	[2]	[6]	[10]
Duaalikappale

Pinta-ala ja tilavuus

Jos ikosidodekaedrin särmän pituus on a, sen pinta-ala (A) ja tilavuus (V) ovat:

${\begin{aligned}A&=\left(5{\sqrt {3}}+3{\sqrt {5}}{\sqrt {3+4\varphi }}\right)a^{2}&&=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&&\approx 29.3059828a^{2}\\V&={\frac {14+17\varphi }{3}}a^{3}&&={\frac {45+17{\sqrt {5}}}{6}}a^{3}&&\approx 13.8355259a^{3}.\end{aligned}}$

Pallopinnan laatoitus

Kuusi kymmenkulmiota ja niiden yhteensä 60 särmää, jotka vastaavat pallopinnan isoympyröitä

Ikosidodekaedri voidaan esittää myös pallopinnan laatoituksena eli sen jakamisena osiin, ja sellaisena se voidaan projisoida tasolle stereografisella projektiolla. Tämä projektio on konformikuvaus eli siinä kulmat pysyvät ennallaan, mutta pituudet ja pinta-alat eivät. Pallopinnan isoympyrät ja näin ollen myös ikosidodekaedrin särmät kuvautuvat tasolle ympyränkaarina.

	keskuksena viisikulmio	keskuksena kolmio
Ortografinen projektio	Stereografiset projektiot

Ortografiset projektiot

Ikosododekaedrin symmetria-akselit, joiden suhteen sillä on kaksin-, kolmin- ja viisinkertaiset symmetriat

Ikosidodekaedri ja muut monitahokkaat

Ikosidodekaedri on suoristettu dodekaedri ja samalla suoristettu ikosaedri, joka saadaan näistä kummastakin säännöllisestä monitahokkaasta leikkaamalla niiden jokaisesta kärjestä pala pois. Ikosidodekaedriin sisältyvät dodekaedrin 12 viisikulmiota ja ikosaedrin 20 kolmiota.

Ikosidodekaedri on myös sukua Johnsonin kappaleisiin kuuluvalle viisikulmaiselle ortobirotundalle, joka saadaan yhdistämällä kaksi viisikulmaista rotundaa, jotka ovat toistensa peilikuvia. Ikosidodekaedria voidaan sen vuoksi nimittää myös viisikulmaiseksi gyrobirotundaksi, sillä se saadaan viisikulmaisesta ortobirotundasta kiertämällä sen ylä- ja alapuoliskoa toistensa suhteen.

(Kahtiajako)

Ikosidodekaedri (viisikullainen gyrobirotunda) Viisikulmainen orthobirotunda Viisikulmainen rotunda

Ikosidodekaedri typistetyssä kuutiossa

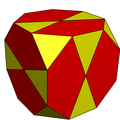
Typistetty kuutio voidaan muuttaa ikosidodekaedriksi jakamalla sen kahdeksankulmiot kukin kahdeksi viisikulmioksi ja kahdeksi kolmioksi. Sillä on pyritoedrinen symmetria.

On olemassa kahdeksan uniformista tähtimonitahokasta, joiden kärjet sijoittuvat toisiinsa nähden samoin kuin ikosidodekaedrissa. Niistä kahdella on ikosidodekaedrin kanssa myös yhteiset särmät: pienellä ikosihemidodekaedrilla (jolla sen kanssa yhteiset kolmiomaiset sivut) ja pienellä dodekahemidodekaedrilla (jolla on sen kanssa yhteiset viisikulmaiset sivut). Ikosidodekaedrin kärkien sijainti on yhteinen myös viiden oktaedrin yhdistelmän sekä viiden tetrahemiheksaedrin kanssa.

Ikosidodekaedri	Pieni ikosihemidodekaedri	Pieni dodekahemidodekaedri
Suuri ikosidodekaedri	Suuri dodekahemidodekaedri	Suuri ikosihemidodekaedri
Dodekadodekaedri	Pieni dodekahemikosaedri	Suuri dodekahemikosaedri
Viiden oktaedrin yhdistelmä	Viiden tetrahemiheksaedrin yhdistelmä

Neliulotteisessa geometriassa

Neliulotteisessa geometriassa ikosidodekaedri esiintyy säännöllisen 600-solun ekvatoriaalisena poikkileikkauksena. Toisin sanoen 600-solun kärjistä ne 30, jotka ovat 90 asteen päässä solun kahdesta vastakkaisesta kärjestä 600-solun ympäri piirretyllä hyperpallolla, ovat ikosidodekaedrin kärjet. Tällaisen 600-solun särmien muodostama kuvio tasolle projisoituna koostuu 72 säännöllisestä kymmenkulmiosta. Kuusi niistä ovvat vastakkaisten kärkien parin määrittelemät ekvatoriaaliset kymmenkulmiot. Juuri nämä kuusi kymmenkulmiota muodostavat ikosidodekaedrin särmien projektiokuvan.

Ikosidodekaedraalinen graafi

Ikosidodekaetrin viisinkertaisesti symmetrinen Schlegelin diagrammi

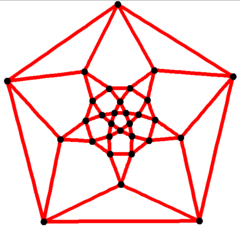
Matemaattisessa graafiteoriassa ikosidodekaedraalinen graafi on ikosidodekaedrin kärkien ja särmien muodosma graafi. Sillä on 30 solmua, joita yhdistää 60 kaarta. Koska ikosidodekaedri kuuluu Arkhimedeen kappaleisiin, sitä vastaava graafi kuuluu Arkhimedeen graafeihin. Sen jokaisessa solmussa kohtaa toisensa neljä kaarta, joten se on neljännen asteen graafi (engl. Quartic graph)

Katso myös

• Kuboktaedri
• Ikosaedri

Lähteet

• Robert Williams: ”Section 3–9”, The Geometrical Foundation of Natural Structure: A Source Book of Design. Dower Publications, Inc., 1979. ISBN 0-486-23729-X
• P. Cromwell: ”Archimedean solids”, Polyhedra, s. 79–86. Cambridge, 1997. ISBN 0-521-55432-2

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Ikosidodekaedri Wikimedia Commonsissa