Diedrinen symmetria kolmessa ulottuvuudessa

Pisteryhmät kolmessa ulottuvuudessa

Involutionaalinen symmetria Cs, (*) [ ] =	Syklinen symmetria Cnv, (*nn) [n] =	Diedrinen symmetria Dnh, (*n22) [n,2] =
Polyedrinen ryhmä, [n,3], (*n32)
Tetraedrinen symmetria Td, (*332) [3,3] =	Oktaedrinen symmetria Oh, (*432) [4,3] =	Ikosaedrinen symmetria Ih, (*532) [5,3] =

Diedrinen symmetria on geometriassa sellaisen kolmiulotteisen kappaleen tai pistejoukon symmetria, jolla on symmetriaryhmänä jokin abstakti diedriryhmä Dih_n ( n ≥ 2 ). Eri tavoin diedrisesti symmetrisiä kappaleita ovat muun muassa särmiöt, bipyramidit, antiprismat ja trapetsoedrit. Tällaiselle kappaleelle voidaan suorittaa jonkin akselin ympäri 360/n asteen rotaatio, jolla se kuvautuu itselleen, toisin sanoen tämä rotaatio on kappaleen symmetriaoperaatio. Lisäksi kappaleen symmetriaoperaatiota saattavat olla peilaukset eräiden tämän akselin kautta kulkevien tai sitä vastaan kohtisuorien tasojen suhteen.

Tyypit

Kolmessa ulottuvuudessa on kolme tyyppiä diedrisiä symmetrioita. Seuraavassa esitetään ne kaikki Schönfliesin, Coxeterin ja orbifoldimerkinnöillä.

Kiraalinen

• D_n, [n,2]⁺, (22n) kertaluvun 2n – diedrinen symmetria eli para-n-kulmainen ryhmä (abstrakti ryhmä Dih_n)

Akiraaliset

• D_nh, [n,2], (*22n), kertaluvun 4n – prismaattinen symmetria eli täysi orto-n-kulmainen ryhmä (abstrakti ryhmä Dih_n × Z₂)
• D_nd (tai D_nv), [2n,2⁺], (2*n), kertaluvun 4n – antiprismaattinen symmetria eli täysi gyro-n-kulmainen ryhmä (abstrakti ryhmä Dih_2n)

Kun luku n on annettu, kaikilla kolmella on n-kertainen pyörähdyssymmetria yhden akselin suhteen (rotaatiossa kulman 360°/n kappale ei muutu), ja kaksinkertainen symmetria kohtisuoran akselin suhteen. Arvolla n = ∞ nämä vastaavat kolmea friisiryhmää. Tässä on käytetty Schönfliesin merkintää sekä Coxeterin symbolia hakasuluissa ja orbifoldimerkintää tavallisissa suluissa. Termiä horisontaalinen (h) käytetään, kun rotaatioakseli on pystysuora.

Kahdessa ulottuvuudessa symmetriaryhmä D_n sisältää peilauksia suorien suhteen. Kun kaksiulotteinen taso on asetettu vaakasuorasti kolmiulotteiseen avaruuteen, tällainen peilaus voidaan käsittää rajoittumaksi joko tämän tason peilauksesta pystysuoran tason suhteen tai 180°:n rotaatiosta peilaussuoran ympäri. Kolmessa ulottuvuudessa nämä ovat kaksi aivan eri operaatiota: ryhmä D_n sisältää vain rotaatiot, ei peilauksia. Saman kertaluvun pyramidaalinen symmetria C_nv muodostaa oman ryhmänsä.

Heijastussymmetrialla n-kertaisen rotaation akselia vastaan kohtisuoran tason suhteen saadaan D_nh [n], (*22n).

Säännöllisiä särmiöitä, joiden symmetriaryhmä on D_nh, missä n on pohjamonikulmion kulmien lukumäärä.

D_nh on säännöllisen n-kulmaisen särmiön ja myös säännöllisen n-sivuisen bipyramidin symmetriaryhmä. D_nd on säännöllisen n-sivuisen antiprisman ja D_n osittain kierretyn särmiön symmetriaryhmä.

Tässä edellytetään, että n on vähintään 2, sillä seuraavat ryhmät ovat samoja:

• D₁ ja C₂ ovat sama kertaluvun 2 ryhmä, johon kuuluu vain 180°:n rotaatio
• D_1h ja C_2v ovat sama kertaluvun 4 ryhmä, johon kuuluvat peilaus tason suhteen ja 180°:n rotaatio tässä tasossa olevan suoran ympäri
• D_1d ja C_2h ovat sama kertaluvun 4 ryhmä, johon kuuluvat peilaus tason suhteen ja 180°:n rotaatio tasoon nähden kohtisuorassa olevan suoran ympäri

Tapauksessa n = 2 ei ole yhtä pääakselia ja kahta lisäakselia vaan kolme keskenään samankaltaista akselia.

• D₂ [2,2]⁺, (222) kertalukua 4 on yksi kolmesta symmetriaryhmätyypistä, jota vastaava abstrakti ryhmä on Kleinin neliryhmä. Sillä on kolme toisiinsa nähden kohtisuoraa kaksinkertaista rotaatioakselia. Se on kuboidin symmetriaryhmä, kun siihen on merkitty S-kirjain kahdelle vastakkaiselle sivulle samoin päin suunnattuina.
• D_2h, [2,2], (*222) kertalukua 8 on kuboidin symmetriaryhmä.
• D_2d, [4,2⁺], (2*2) kertalukua 8 on muun muassa seuraavien kappaleiden symmetriaryhmä:
• neliökuboidi, jonka yhteen neliömäiseen sivuun on piirretty lävistäjä ja toiseen sivuun sitä vastaan kohtisuora lävistäjä;
• säännöllinen tetraedri, joka on venytetty kahden vastaakkaisen sivun keskipisteiden välisen janan suunnassa (D_2d on tetraedrisen symmetrian T_d aliryhmä); skaalauksella vähennetään symmetriaa.

Aliryhmät

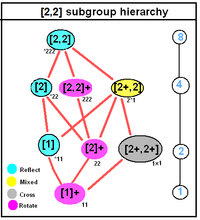D2h, [2,2], (*222), aliryhmien hierarkia

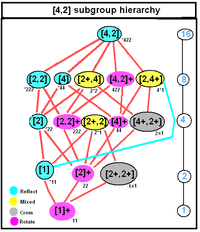D4h, [4,2], (*224), aliryhmien hierarkia

Ryhmällä D_nh, [n,2], (*22n), kertalukua 4n, on seuraavat aliryhmät:

• C_nh, [n⁺,2], (n*), kertalukua 2n
• C_nv, [n,1], (*nn), kertalukua 2n
• D_n, [n,2]⁺, (22n), kertalukua 2n

Ryhmällä D_nd, [2n,2⁺], (2*n), kertalukua 4n, on seuraavat aliryhmät:

• S_2n, [2n⁺,2⁺], (n×), kertalukua 2n
• C_nv, [n⁺,2], (n*), kertalukua 2n
• D_n, [n,2]⁺, (22n), kertalukua 2n

D_nd on myös ryhmän D_2nh aliryhmä.

Esimerkkejä

D2h, [2,2], (*222) Kertaluku 8	D2d, [4,2+], (2*2) Kertaluku 8	D3h, [3,2], (*223) Kertaluku 12
koripallon saumat	baseball-pallon saumat (kun saumausten suuntia ei oteta huomioon)	rantapallo (kun värejä ei oteta huomioon)

D_nh, [n], (*22n):

särmiöitä

D_5h, [5], (*225):

pentagrammipohjainen särmiö

pentagrammipohjainen antiprisma

D_4d, [8,2⁺], (2*4):

pullistettu neliöpohjainen antiprisma

D_5d, [10,2⁺], (2*5):

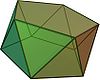viisikulmainen antiprisma

viisikulmainen risteävä antiprisma

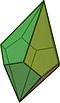pentagonaalinen trapetsoedri

D_17d, [34,2⁺], (2*17):

17-kulmainen antiprisma

Lähteet

• H. S. M. Coxeter, W. O. J. Moser: Generators and Relations for Discrete Groups. New York: Springer-Verlag, 1980. ISBN 0-387-09212-9
• N. W. Johnson: ”Chapter 11:5: Finite symmetry groups: Spherical Coxeter Groups”, Geometries and Transformations. Määritä julkaisija! ISBN 978-1-107-10340-5
• John Horton Conway, Dabiel H. Huson: The Orbifold Notation for Two-Dimensional Groups. Structural Chemistry, 2002, 13. vsk, nro 3, s. 247–257. Springer Netherlands. doi:10.1023/A:1015851621002

Aiheesta muualla

• Symmetry: Solids (Kuvia eri tavoin diedrisesti symmetrisistä kappaleista) University of Exeter. Viitattu 15.7.2020.