Antiprisma

Uniformisten antiprismojen joukko
Tyyppi	uniforminen monitahokas
Tahkoja	2 n-kulmiota, 2n kolmiota
Särmiä	4n
Kärkiä	2n
Conwayn monitahokasmerkintä	An
Kärkikuvio	3.3.3.n
Schläflin symboli	{ }⊗{n} s{2,2n} sr{2,n}
Coxeterin diagrammit
Symmetriaryhmä	Dnd, [2+,2n], (2*n), kertaluku 4n
Rotaatioryhmä	Dn, [2,n]+, (22n), kertaluku 2n
Duaalimonitahokas	Trapetsoedri
Ominaisuudet	kupera, semiregulaarinen, kärkitransitiivinen
Verkko

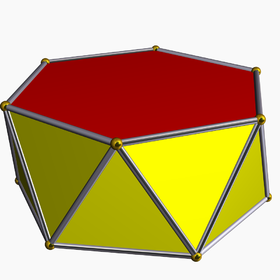
Antiprisma on geometriassa monitahokas, jonka muodostaa kaksi keskenään yhtenevää, yhden­suuntaisille tasoille asetettua monikulmiota, joita sanotaan antiprisman pohjiksi ja joita yhdistää toisiinsa vuorotteleva nauha kolmioita. Jos pohjat ovat n-kulmioita, sanotaan antiprismaa n-sivuiseksi antiprismaksi.

Antiprismat ovat prismatoidien alaluokka, ja ne voidaan myös katsoa surkastuneiksi erikois­tapaukseksi pullistetuista moni­tahokkaista.

Antiprismat muistuttavat muutoin särmiöitä, paitsi että niiden pohjia on kierretty toistensa suhteen ja että niiden sivutahkot eivät ole suunnikkaita vaan kolmioita.

Jos pohja on säännöllinen n-kulmio, erityisen huomattava on antiprisma, jonka pohjia on kierretty toisiinsa kulman ⁠180°/n⁠ verran. Vielä säännöllisempi antiprisma saadaan, jos pohjien keskipisteet toisiinsa yhdistävä jana on kohtisuorassa pohjatasoihin nähden, jolloin kyseessä on suora antiprisma. Sillä on tahkoina kaksi n-kulmiota, joita yhdistää 2n tasakylkistä kolmiota.

Uniformiset antiprismat

Antiprismaa sanotaan uniformiseksi, jos sen kaikki tahkot ovat säännöllisiä monikulmioita. Jos sen pohjat ovat säännöllisiä n-kulmioita, muina tahkoina sillä on 2n tasasivuista kolmiota. Uniformiset antiprismat muodostavat äärettömän sarjan uniformisia monitahokkaita, samoin kuin uniformiset särmiötkin.

Tapauksessa n = 2 vastaava särmiö on surkastunut, mutta antiprismaksi saadaan erikoistapauksena, kaksikulmaisena antiprismana, säännöllinen tetraedri. Tapauksessa n = 3 saadaan kolmikulmaiseksi antiprismaksi säännöllinen oktaedri.

Uniformisia antiprismoja

Antiprisman nimi	Kaksikulmainen (digonaalinen) antiprisma (tetraedri)	Kolmikulmainen (trigonaalinen) antiprisma (oktaedri)	Nelikulmainen (tetragonaalinen) antiprisma	Viisikulmainen (pentagonaalinen) antiprisma	Kuusikulmainen (heksagonaalinen) antiprisma	Seitsenkulmainen (heptagonaalinen) antiprisma	...	Apeirogonaalinen antiprisma
Monitahokkaan kuva
Vastaava pallopinnan laatoitus
Kärkikonfiguraatio	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3		∞.3.3.3

Antiprismojen duaalikappaleet

Antiprismojen duaalikappaleita ovat trapetsoedrit. Niitä tutki tiettävästi ensimmäisenä Johannes Kepler, joka myös antoi niille nimen, joskin on mahdollista, että jo Arkhimedes tunsi ne, sillä niiden kärjet toteuttavat samat ehdot kuin Arkhimedeen kappaleet.

Schlegelin diagrammit

A3

A4

A5

A6

A7

A8

Karteesiset koordinaatit

Jos suoran n-kulmaisen antiprisman sivutahkot ovat tasakylkisiä kolmioita, sen kärkien karteesiset koordinaatit ovat:

$\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)$

missä k saa kaikki kokonaislukuarvot välilt 0...2n - 1. Jos sivutahkot ovat tasasivuisia kolmiota, on

$2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.$

Pinta-ala ja tilavuus

Olkoon a uniformisen antiprisman sirämän pituus. Silloin kappaleen tilavuus on

$V={\frac {1}{12}}na^{2}(\cot {\frac {\pi }{2n}}+\cot {\frac {\pi }{n}}){\sqrt {1-{\frac {1}{4\cos ^{2}{\frac {\pi }{2n}}}}}}$,

ja sen tahkojen yhteenlaskettu pinta-ala on

$A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.$

Antiprismoista johdettuja monitahokkaita

On olemassa ääretön joukko typistettyjä antiprismoja, muun muassa vähemmän symmetrinen muoto typistetystä oktaedrista (typistetty kolmikulmainen antiprisma). Ne voidaan alternoida niin, että saadaan pullistettuja antiprismoja. Niistä kaksi kuuluu Johnsonin kappaleisiin, ja typistetty kolmikulmainen antiprisma on vähemmän symmetrinen muoto säännöllisestä ikosaedrista.

Antiprismoja
				...
s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,2n}
Typistettyjä antiprismoja
				...
ts{2,4}	typistetty oktaedri ts{2,6}	ts{2,8}	ts{2,10}	ts{2,2n}
Pullistettuja antiprismoja
Pullistettu disfenoidi J84	Säännöllinen ikosaedri	Pullistettu antiprisma J85	Epäsäännölliset...
				...
ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}	{2,2n}

Symmetria

Sellaisen suoran n-kulmaisen antiprisman symmetriaryhmä, jonka pohja on säännöllinen monikulmio ja sivutahkoina tasakylkiset kolmiot, on D_nd kertalukua 4n. Poikkeuksena ovat tetraedri, jolla on laajempi symmetriaryhmä T_d kertalukua 24, johon sisältyy aliryhminä kolme versiota ryhmästä D_2d, sekä oktaedri, jonka symmetriaryhmä O_h on kertalukua 48 ja sisältää aliryhminään kolme versiota ryhmästä D_3d.

Peilaus pisteen suhteen eli inversio kuuluu symmetriaryhmään, jos ja vain jos n on pariton.

Anriprisman rotaatioryhmä on D_n kertalukua 2n. Poikkeuksena ovat tetraedri, jolla on laajempi rotaatioryhmä T kertalukua 12 sisältäen aliryhminään kolme versiota ryhmästä D₂, sekä oktaedri, jolla on laajempi rotaatioryhmä O kertalukua 24 sisältäen aliryhminään neljä versiota ryhmästä D₃.

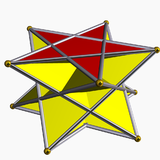
Tähtiantiprismat

5/2-antiprisma			5/3-antiprisma
9/2-antiprisma		9/4-antiprisma		9/5-antiprisma

Kuvassa ovat kaikki tähtimäiset ja ei-tähtimäiset 3–15-sivuiset antiprismat sekä lisäksi 29-sivuinen antiprisma

Uniformisia tähtiantiprismoja nimetään niiden pohjana olevien tähtimonikulmioiden {p/q} mukaan. Niitä on kahta tyyppiä: eteneviä (engl. prograde) ja takautuvia (engl. retrograde eli leikattuja. Takautuvilla muodoilla kärkikuviot leikkaavat toisensa, ja niitä merkitään muotoa p/(p - q) olevilla murtoluvuilla murtolukujen p/q sijasta, esimerkiksi 5/3 luvun 5/2 sijasta.

Takautuvissa antiprismoissa kolmiomaiset sivutahkot, jotka yhdistävät pohjat toisiinsa, leikkaavat rotaatiosymmetria-akselin. Etenevissä antiprismoissa näin ei ole laita.

Joitakin tähtiantiprismoja, joiden pohjana on säännöllinen tähtimonikulmio, ei voida konstruoida niin, että kaikki särmät olisivat yhtä pitkät, ja näin ollen ne eivät ole uniformisia monitahokkaita. Tähtiantiprismaojen komponentit voidaan myös konstruoida, kun luvuilla p ja q on yhteisiä tekijöitä; niinpä antiprisma 10/4 on kahden 5/2 -antiprisman yhdistelmä.

Seuraavassa taulukossa on kuvattu tähtiantiprismat 12-kulmaisiin saakka sekä niiden pohjakuviot ja merkinnät.

Tähtiantiprismat symmetrian mukaan
Symmetriaryhmä	Uniformiset tähdet				Muut tähdet
d4d [2+,8] (2*5)					neliö 3.3/2.3.4
d5h [2,5] (*225)	Pentagrammi 3.3.3.5/2				Viisikulmio 3.3/2.3.5
d5d [2+,10] (2*5)	Pentagrammi 3.3.3.5/3
d6d [2+,12] (2*6)		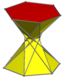			Kuusikulmio 3.3/2.3.6
d7h [2,7] (*227)	Heptagrammi (7/2) 3.3.3.7/2	Heptgrammi (7/4) 3.3.3.7/4
d7d [2+,14] (2*7)	Heptagrammi (7/3) 3.3.3.7/3
d8d [2+,16] (2*8)	Oktagrammi (8/3) 3.3.3.8/3	Oktagrammi (8/5) 3.3.3.8/5
d9h [2,9] (*229)	Enneagrammi (9/2) 3.3.3.9/2	Enneagrammi (9/4)3.3.3.9/4
d9d [2+,18] (2*9)	Enneagrammi (9/4)
d10d [2+,12] (2*10)	Dekagrammi (10/3) 3.3.3.10/3
d11h [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
d11d [2+,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
d12d [2+,24] (2*12)	Dodekagrammi (12/5) 3.3.3.12/5	Dodekagrammi (12/7)3.3.3.12/7
...

Antiprima arkkitehtuurissa

One World Trade Center (kuvassa keskellä)

One World Trade Center New Yorkissa on pitkänomainen neliöpohjaisen antiprisman muotoinen pilvenpiirtäjä.

Lähteet

• Anthony Pugh: ”Ch 2: Archimedean polyhedra, prisma and antiprisms”, Polyhedra: A visual approach. Berkeley: University of California Press. ISBN 0-520-03056-7

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Antiprisma Wikimedia Commonsissa