Matematiikka
| Tähän artikkeliin tai osioon ei ole merkitty lähteitä, joten tiedot kannattaa tarkistaa muista tietolähteistä. Voit auttaa Wikipediaa lisäämällä artikkeliin tarkistettavissa olevia lähteitä ja merkitsemällä ne ohjeen mukaan. |

Matematiikka on deduktiiviseen päättelyyn perustuva formaali eli käsitteellinen tiede. Matematiikassa tutkitaan muun muassa lukuja, määriä, rakenteita, muutoksia ja avaruuksia. Matemaattisen formalismin mukaan matematiikka on aksiomaattisesti määriteltyjen abstraktien rakenteiden tutkimista symbolisen logiikan ja matemaattisen merkintäjärjestelmän keinoin. Matematiikkaa käytetään fysikaalisten ja käsitteellisten suhteiden ilmaisemisen kielenä, jonka kielioppi ja käsitteistö on määritelty äärimmäisen tarkkaan. Tämä mahdollistaa asioiden ilmaisemisen yksikäsitteisesti, kun oletetaan loogisten rakenteiden pysyvän muuttumattomina.
Matematiikka ei tutki ympäröivää, fysikaalista todellisuutta, vaan käsitteellisiä riippuvuussuhteita. Tämän takia sitä ei yleensä lueta luonnontieteisiin, vaikka matematiikan ja matemaattisten menetelmien soveltaminen on tärkeä osa luonnontieteitä ja monet matematiikan tutkimusongelmat ovat peräisin luonnontieteistä, erityisesti fysiikasta. Esimerkiksi Isaac Newtonin kehittämä mekaniikka ja painovoimateoria vaikutti suuresti differentiaali- ja integraalilaskennan kehittymiseen.
Matematiikalla on luonnontieteiden lisäksi paljon sovelluskohteita myös esimerkiksi tekniikan ja teknologian eri aloilla, yhteiskuntatieteissä ja taloustieteessä. Toisaalta matematiikassa tutkitaan myös puhtaasti matematiikan sisäisiä alueita, joille ei välttämättä ainakaan heti ole sovellusalueita millään muulla tieteenalalla. Nykyään matemaattinen tutkimus esimerkiksi korkeakouluissa usein jaetaankin tällaiseen puhtaaseen matematiikkaan ja soveltavaan matematiikkaan, joka tutkii matematiikan soveltamista käytännön ongelmiin, mutta tarkkaa rajaa puhtaan ja soveltavan matematiikan välille on vaikea vetää.
Myös eläimillä on havaittu olevan kykyä oppia matemaattisia taitoja. Esimerkiksi mehiläiset kykenevät suorittamaan yksinkertaisia yhteen- ja vähennyslaskuja. Ne ymmärtävät myös suuruusjärjestyksen käsitteen sekä pystyvät erottamaan parittomat lukumäärät parillisista eli kahdella jaollisista lukumääristä.[1] Jotkin varislinnut ymmärtävät nollan käsitteen.[2]
Etymologia ja yleiskatsaus
[muokkaa | muokkaa wikitekstiä]Sana matematiikka (kreik. μαθηματικά, ’mathēmatiká’) tulee kreikan sanasta μάθημα (máthēma), joka tarkoittaa tiedettä, tietoa tai oppimista. Matemaatikkoa tarkoittava kreikankielinen sana μαθηματικός (mathematikós) tarkoittaa ”halukas oppimaan”.
Matematiikan pääalueet syntyivät käytännön tarpeista. Laskutaito oli tarpeellinen niin kaupankäynnissä, maanmittauksessa kuin tähtitieteellisten tapahtumien ennustamisessakin. Matematiikka on siis alun perin muiden tieteiden (lähinnä luonnontieteiden) työkalu ja tutkimustulosten tarkka ilmaisuväline. Matematiikan avulla voidaan teoreettisesti tarkastella käytännössä havaittuja asioita ja tehdä näistä tutkimustuloksista johtopäätöksiä. Kuitenkin jo antiikin Kreikassa tunnettiin ajatus matematiikan kauneudesta.[3]
Matematiikan vanhimpia osa-alueita ovat aritmetiikka eli laskuoppi sekä geometria. Aritmetiikka käsittelee numeroita ja lukuja, joista ensimmäisenä on otettu käyttöön positiiviset kokonaisluvut eli luonnolliset luvut, sekä niillä suoritettavia laskutoimituksia. Lukukäsitteen myöhemmät laajennukset ovat johtaneet muidenkin lukulajien kuten reaalilukujen ja kompleksilukujen käyttöönottoon. Lukuteoria tutkii lukujen syvempiä ominaisuuksia. Yhtälöiden ratkaisemisessa tarvittavien menetelmien tutkimus johtaa algebraan.
Avaruuksien tutkiminen saa alkunsa geometriasta. Ensin kehitettiin euklidinen geometria, josta trigonometria on eriytynyt omaksi erikoisalakseen. Myöhemmin osoittautui, ettei euklidinen geometria ole ainoa looginen mahdollisuus, ja sen ohella onkin kehitetty myös epäeuklidisia geometrioita.
Nykyisen korkeamman matematiikan pääosiksi mainitaan tavallisesti abstrakti algebra, analyysi ja topologia, jotka jakaantuvat moniin osa-alueisiin. Matematiikan peruskäsitteiden tarkempi analysointi on johtanut joukko-opin kehittymiseen.
Matemaatikot loivat lukuisia välttämättömiä käsitteitä tietokoneita kehitettäessä; näistä kehittyi edelleen informaatioteoria.
Historia
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Matematiikan historia
Matematiikan historia on hyvin pitkä. Matematiikka on fysiikan ja tähtitieteen ohella vanhimpia tieteenaloja.
Matematiikan ensimmäisten vaiheiden tarkka selvittäminen on mahdotonta, sillä ihmiskunta oppi laskemaan ennen kirjoitustaidon syntyä. Niinpä mitään kirjallisia dokumentteja ensimmäisistä laskusäännöistä tai geometrisista hahmotelmista ei ole jäljellä. Matematiikan varhaishistoriaa voidaan tutkia parhaiten arkeologisten löytöjen, kielitieteen ja eläinten tarkkailun avulla. On todettu, että monet eläimet kykenevät erottamaan ainakin viittä alkiota pienempien joukkojen kokoeron. Siten voidaan olettaa, että jonkinlainen luvun käsite on hyvin vanha. Tätä tukee myös monien kielten kieliopillisen luvun jaottelu yhteen ja moneen, jossain tapauksessa kahteen ja kolmeenkin.
Siitä, että on ymmärretty kahden kiven ja kolmen kiven välinen ero, on ollut todennäköisesti pitkä matka siihen, että on ymmärretty abstraktin käsitteen ”kolme” liittävän yhteen kolme kiveä ja kolme puuta.[3][4] Tätä ajatusta tukee se, että monet joukkojen kokoeroja hahmottavat eläimet eivät pysty tähän. Lisäksi ensimmäiset kieliin ilmaantuneet lukusanat ovat tarkoittaneet alun perin esimerkiksi kahta kiveä. Lukua on siis ollut vaikea hahmottaa yhteydestään irrallisena käsitteenä. Joidenkin teorioiden mukaan järjestysluvut olisivat syntyneet ennen kardinaalilukuja. Tätä on perusteltu sillä, että monissa rituaaleissa ja myyteissä tapahtumien ja henkilöiden järjestyksellä on ollut tärkeä osa.[4] Kielet eivät kuitenkaan tue tätä käsitystä, sillä lähes kaikissa kielissä järjestysluvut muodostetaan kardinaalilukusanojen johdannaisina.
Vanhimmat arkeologiset todisteet lukumäärien laskennasta ovat noin 30 000 vuotta vanhoja. Tšekistä löydetyssä luussa on yhteensä 55 lovea, jotka on jaoteltu viiden ryhmiin. Viisi on ollut luonnollinen valinta sopivaksi joukoksi, koska sormia on yhdessä kädessä viisi. Kymmenen (kahden käden sormet) ja kaksikymmentä (sormet ja varpaat) ovat olleet myös varhaisia lukujärjestelmien kantalukuja. Amerikan intiaaniheimoille tehdyssä tutkimuksessa kolmannes käytti viisijärjestelmää, kolmannes kymmenjärjestelmää, vajaa kolmannes binaarijärjestelmää ja loput kolmijärjestelmää. Kaksikymmenjärjestelmästä on todisteita lähinnä Euroopasta, missä sen jäänteitä näkyy yhä kielissä, ranskan 80 (quatre-vingt) on suomeksi neljä kahtakymmentä. Varhaisimmat kirjoitetut todisteet näyttävät suosineen viisijärjestelmää, mutta kielen saadessa selvän formaalisen muodon kymmenjärjestelmä on noussut yleisimmäksi.[4]
Geometrian varhaisvaiheita on lukujen syntyäkin vaikeampi selvittää. Kreikkalaiset sijoittivat geometrian synnyn muinaiseen Egyptiin, jossa sitä tarvittiin maanmittaukseen. On kuitenkin selvää, ettei kehittynyt geometrinen ajattelu ole syntynyt tuolloin tyhjästä, vaan jo paljon aiemmin on ollut jonkinlaista geometrista hahmotuskykyä. Monet muutkin eläimet, etenkin apinat, pystyvät hahmottamaan muodon abstraktina, tietystä esineestä irrallisena asiana ja ryhmittelemään eri esineitä muodon perusteella ryhmiin.
Vanhimmat todisteet luovasta geometrisesta ajattelusta voidaan nähdä geometrisia kuvioita esittävissä luolamaalauksissa ja erilaisissa punostöissä. Jo niissä on nähtävissä esimerkiksi ajatus kuvioiden yhdenmuotoisuudesta ja symmetriasta.[5]
Matematiikan filosofia
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Matematiikan filosofia
Matematiikan filosofia on filosofian osa-alue, joka tutkii matematiikan filosofisia perusteita, oletuksia ja seurauksia.
Matematiikan filosofian teemoja ovat muun muassa:
- Mikä on matemaattisten olioiden ontologinen luonne?
- Mitä matemaattiseen olioon viittaaminen tarkoittaa?
- Mikä on matemaattisen väittämän luonne?
- Mikä on matemaattisen totuuden luonne?
- Minkälaista tutkimusta matematiikassa tulisi suorittaa?
- Mikä on matematiikan ja logiikan suhde?
- Miksi ja millä tavalla matematiikka on hyödyllistä tieteelle?
- Mitä on matemaattinen kauneus?
Tärkeitä teemoja matematiikassa
[muokkaa | muokkaa wikitekstiä]Seuraava lista antaa vain yhden mahdollisen näkemyksen.
Kvantiteetti
[muokkaa | muokkaa wikitekstiä]- Kvantiteetti lähtee liikkeelle laskemisesta ja mittaamisesta.
Rakenne
[muokkaa | muokkaa wikitekstiä]- Ajatuksia koosta, symmetriasta ja matemaattisesta rakenteesta.
- Algebralliset struktuurit.
Avaruus
[muokkaa | muokkaa wikitekstiä]- Visuaalisempi lähestymistapa matematiikkaan.
Muutos
[muokkaa | muokkaa wikitekstiä]- Tapa ilmaista ja käsitellä muutosta matemaattisissa funktioissa ja lukujen välillä.
Perusteet ja metodit
[muokkaa | muokkaa wikitekstiä]- Lähestymistapoja, joiden avulla voi ymmärtää matematiikan luonnetta.
Diskreetti matematiikka
[muokkaa | muokkaa wikitekstiä]- Diskreetti matematiikka sisältää tekniikoita, jotka pätevät objekteihin, joilla voi olla vain tiettyjä, erillisiä arvoja.
Sovellettu matematiikka
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Sovellettu matematiikka
- Sovellettu matematiikka pyrkii ratkaisemaan tosielämän ongelmia matematiikkaan liittyvien eri osa-alueiden avulla.
- Matemaattinen fysiikka – Mekaniikka – Numeerinen analyysi – Todennäköisyys – Tilastotiede – Matemaattinen talous – Finanssimatematiikka – Peliteoria – Matemaattinen biologia – Kryptografia – Tietokoneavusteinen matematiikka
Tärkeitä teoreemoja
[muokkaa | muokkaa wikitekstiä]- Nämä teoreemat ja olettamukset ovat kiinnostaneet matemaatikkoja ja ei-matemaatikkoja.
- De Moivren kaava – Eulerin lause – Fermat'n suuri lause – Goldbachin väittämä – Poincarén väittämä – Pythagoraan lause – Riemannin hypoteesi
Tärkeitä konjektuureja
[muokkaa | muokkaa wikitekstiä]- Nämä kuuluvat matematiikan suurimpiin ratkaisemattomiin ongelmiin. Katso myös luettelo ratkaisemattomista matemaattisista ongelmista.
- Goldbachin konjektuuri – Riemannin hypoteesi – Collatzin konjektuuri – P=NP? – avoimet Hilbertin ongelmat.
Sekalaisia
[muokkaa | muokkaa wikitekstiä]- aksiooma – funktio – joukko – kommutatiivisuus – kunta – lause – lemma – luku – numero – osajoukko – otaksuma – relaatio – rengas – ryhmä – lause – yhtälö
Alkioita eri avaruuksissa
[muokkaa | muokkaa wikitekstiä]- algebrallinen luku – alkuluku – imaginaariluku – irrationaaliluku – kokonaisluku – kompleksiluku – luonnollinen luku – matriisi – murtoluku – rationaaliluku – reaaliluku – transsendenttiluku – vektori
Tutkimusalueita
[muokkaa | muokkaa wikitekstiä]- algebra – analyysi – aritmetiikka – diskreetti matematiikka – fraktaaligeometria – funktioteoria – geometria – joukko-oppi – lineaarialgebra – logiikka – lukuteoria – numeeriset menetelmät – peliteoria – ryhmäteoria – tilastotiede – todennäköisyys – topologia – verkkoteoria
Katso myös
[muokkaa | muokkaa wikitekstiä]- Ajanvietematematiikka
- Digitaalinen signaalinkäsittely
- Luettelo matemaatikoista
- Luettelo ratkaisemattomista matemaattisista ongelmista
- Mallintaminen
- Matemaattinen merkintä
- Tiede ja matematiikka
Lähteet
[muokkaa | muokkaa wikitekstiä]- Boyer, Carl B. & Merzbach, Uta C.: Tieteiden kuningatar – Matematiikan historia, osa I. (A history of mathematics, 1985.) Suomentanut Kimmo Pietiläinen. Helsinki: Art House, 1994. ISBN 951-884-150-0
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ Eläintiede | Mehiläinen tajuaa parillisen ja parittoman – vain ihmisen on tiedetty pystyvän samaan suoritukseen Helsingin Sanomat. 22.6.2022. Viitattu 23.6.2022.
- ↑ Eläintiede | Varis osoittautui todella älykkääksi siivekkääksi, sillä lintu ymmärsi jopa nollan merkityksen Helsingin Sanomat. 4.8.2021. Viitattu 16.5.2024.
- ↑ a b Matematiikan kauneus sykähdyttää mutta avautuu vain harvoille | Tieteessä tapahtuu www.tieteessatapahtuu.fi. Viitattu 24.8.2023.
- ↑ a b c Boyer, osa I s. 23–29
- ↑ Boyer, osa I s. 29–31
Kirjallisuutta
[muokkaa | muokkaa wikitekstiä]- Bentley, Peter J.: Numerot: Kuinka matematiikka muutti maailmaa. (The book of numbers, 2008.) Suomentanut Tommi Uschanov. Helsinki: Ajatus, 2009. ISBN 978-951-20-7632-1
- Karttunen, Hannu: Matematiikka. (Tiedettä kaikille. Ursan julkaisuja 99) Helsingissä: Tähtitieteellinen yhdistys Ursa, 2006. ISBN 952-5329-48-8
- Kivelä, Simo K.: M niinkuin matematiikka: Lukiotason matematiikan tietosanakirja. 2. tarkistettu painos. Jyväskylä: MFKA-kustannus, 2000. ISBN 952-9656-57-2 Teoksen verkkoversio.
- Stewart, Ian: Kirjeitä nuorelle matemaatikolle. (Letters to a young mathematician, 2006.) Suomentanut Juha Pietiläinen. Helsinki: Terra Cognita, 2007. ISBN 978-952-5697-02-5
- Thompson, Jan; Martinsson, Thomas (toim.): Matematiikan käsikirja. (436 sivua) Helsinki: Tammi, 1994. ISBN 951-31-0471-0
- Bell, Eric Temple: Men of Mathematics. Simon & Schuster, 1965. ISBN 0-671-62818-6
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä]- Makupalat-linkkikirjaston matematiikkalinkit
- Matematiikkalehti Solmu
- Matematiikkalehti Solmu – Matematiikan historia. Kirjoittanut dosentti Matti Lehtinen.
- Matematiikkalehti Solmu: Matematiikan verkkosanakirja
- Ylen Elävä arkisto – Matematiikka (2004) (audio)
- Ylen Elävä arkisto – Matematiikka osana kulttuuria (2004) (audio)
- Matemaattiset aineet (Opintoluotsi)
- Matematiikkaa Geogebra-ohjelmalla luotua materiaalia
- Math – Khan Academy (englanniksi)
- Maailmankaikkeuden kieli ei avaudu kaikille yhtä helposti








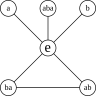













![{\displaystyle [1,2,3][1,3,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3456de48f67f15147542c745a3a8cbe64d9ed7e)
![{\displaystyle [2,1,3][2,3,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2982b802b037da0f46b428d63581818291e5a8bd)
![{\displaystyle [3,1,2][3,2,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fd3d1378424e83c7f56eef8db2ea044b149c25a)

