Tason yhtenevyyskuvaus

Tason yhtenevyyskuvaus eli tason isometria on geometriassa euklidisen tason yhtenevyyskuvaus itselleen eli kuvaus, jossa taso­kuvioiden geometriset ominaisuudet kuten janojen pituus ja kulmat säilyvät. Tason yhtenevyys­kuvauksia on neljää tyyppiä: yhden­suuntais­siirto eli translaatio, kierto eli rotaatio (geometria), peilaus suoran suhteen sekä peilauksen ja translaation yhdistettynä kuvauksena muodostettu liukupeilaus. Joskus mainitaan yhtenä yhtenevyys­kuvauksen tyyppinä myös peilaus pisteen suuntaan, joka kuitenkin on sama kuin 90 asteen kierto.

Euklidisen tason yhtenevyys­kuvaukset muodostavat ryhmän, kaksi­ulotteisen euklidisen ryhmän, jossa lasku­toimituksena on kuvausten yhdistäminen. Jokainen tason yhtenevyys­kuvaus voidaan muodostaa yhdistettynä kuvauksena enintään kolmesta peilauksesta suorien suhteen.

Translaatiossa ja rotaatiossa säilyy myös kätisyys, peilauksessa ja liuku­peilauksessa sen sijaan ei, vaan niissä kuvio muuttuu peilikuvakseen tai sen kaltaiseksi.

Havainnollisia esimerkkejä

Tason yhtenevyys­kuvauksia ovat kaikki tavat, joilla tasoa voidaan muuntaa ilman kuvioiden koon tai muodon muutoksia. Voidaan esimerkiksi kuvitella, että tasoa esittää läpi­näkyvä muovi­kalvo pöydällä. Esimerkkejä yhtenevyys­kuvauksista ovat tällöin:

• siirretään muovi­kalvoa 10 cm oikealle
• kierretään muovi­kalvoa 10 astetta jonkin merkityn pisteen ympäri, joka itse pysyy paikoillaan
• käännetään muovi­kalvo ylös­alaisin nostamalla se välillä pois pöydältä. On huomattava, että jos kalvon toiselle puolelle on piirretty jokin kuvio, sen kääntämisen jälkeen kuvio näkyy peilikuvanaan.

Edellä mainitut ovat esimerkkejä translaatiosta, rotaatiosta ja peilauksesta. Näiden lisäksi on vielä yksi yhtenevyys­kuvausten tyyppi, jota sanotaan liuku­peilaukseksi (engl. glide reflection) ja jota käsitellään tarkemmin jäljempänä.

Sen sijaan kalvon taittaminen, leikkaaminen tai sulattaminen eivät vastaa yhtenevyys­kuvauksia, eivät myöskään sen taivuttaminen, venyttäminen tai vääntäminen mutkalle.

Muodollinen määritelmä

Euklidisen tason isometria on etäisyydet säilyttävä kuvaus tasolta itselleen. Toisin sanoen se on kuvaus

$M:{\textbf {R}}^{2}\to {\textbf {R}}^{2}$

jossa jokaiselle tason pisteparille p, q pätee

$d(p,q)=d(M(p),M(q)),\,\!$

missä d(p, q) on pisteiden p ja q välinen tavanomainen euklidinen etäisyys.

Tason yhtenevyyskuvausten luokittelua

Voidaan osoittaa, että tason yhtenevyys­kuvauksia on neljää tyyppiä. On huomattava, että alla olevat kuvaus­tyyppien merkinnät eivät ole täysin standardoituja.

• Translaatio, jolle käytetään merkintää T_v missä v on $\mathbb {R} ^{2}$:n vektori. Tämän vaikutus on, että taso siirtyy v:n suuntaan. Ninpä jokaiselle tason pisteelle p on

$T_{v}(p)=p+v,\,\!$

tai (x, y)-koordinaatistossa,

$T_{v}(p)={\begin{bmatrix}p_{x}+v_{x}\\p_{y}+v_{y}\end{bmatrix}}.$

• Rotaatio, jolle käytetään merintää R_c,θ, missä θ on se tason piste, jonka ympäri tasoa kierretään ja θ kiertokulma. Koordi­naatis­tossa rotaatio voidaan helpoimmin ilmaista muodostamalla se kahdesta operaatiosta. Ensiksikin rotaatiota origon ympäri esittää yhtälö

$R_{0,\theta }(p)={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}{\begin{bmatrix}p_{x}\\p_{y}\end{bmatrix}}.$

Nämä matriisit ovat orto­gonaalisia matriiseja, joiden determinantti on 1. Toisin sanoen ne ovat sellaisia neliö­matriiseja G, joiden on transpoosi on sama kuin sen käänteismatriisi eli $GG^{T}=G^{T}G=I_{2}.$. (Orto­gonaalisen matriisin determinantti voi olla myös −1; tällaiset tapaukset vastaavat peilauksia, kuten jäljempänä todetaan.) Rotaatiot origon ympäri muodostavat myös ryhmän, orto­gonaalisen ryhmän SO(2).

Rotaatio pisteen c ympäri voidaan muodostaa suorittamalla ensin translaatio, jossa c kuvautuu origoon, sitten rotaatio origon ympäri ja lopulta toinen translaatio, jossa origo kuvautuu jälleen pisteeseen c. Tosin sanoen

$R_{c,\theta }=T_{c}\circ R_{0,\theta }\circ T_{-c},$

eli

$R_{c,\theta }(p)=c+R_{0,\theta }(p-c).\,\!$

Vaihtoehtoisesti voidaan suorittaa ensin rotaatio origon ympäri ja sitten translaatio:

$R_{c,\theta }(p)=R_{0,\theta }p+v.\,\!$

• Peilaus eli peili-isometria, jolle käytetään merkintää F_c,v, missä c on tason piste ja v $\mathbb {R} ^{2}$:n yksikkövektori. Tämä peilaa pisteen o suoran L suhteen, joka on kohti­suorassa v:tä vastaan ja kulkee c:n kautta. Suoraa L sanotaan peilaus­akseliksi. Jotta F_c,v:lle löytyisi kaava,p − c:n komponentti t vektorin v suunnassa määritetään pistetulon avulla,

$t=(p-c)\cdot v=(p_{x}-c_{x})v_{x}+(p_{y}-c_{y})v_{y},$

minkä jälkeen p:n peilaus saadaan vähennys­laskulla

$F_{c,v}(p)=p-2tv.\,$

Jokaista rotaatiota origon ympäri ja peilausta origon kautta kulkevan suoran suhteen vastaa jokin orto­gonaalinen matriisi, jonka determi­nantti on joko 1 tai −1, ja kääntäen. Nämä muodostavat orto­gonaalisen ryhmän O(2). Niissä tapauksissa, joissa determi­nantti on −1, saadaan:

$R_{0,\theta }(p)={\begin{pmatrix}\cos \theta &\sin \theta \\\sin \theta &-\cos \theta \end{pmatrix}}{\begin{bmatrix}p_{x}\\p_{y}\end{bmatrix}}.$

mikä voidaan muodostaa yhdistämällä peilaus x-akselin suhteen ja rotaatio kulman θ verran, tai yhtäpitävästi peilaus sellaisen suoran suhteen, joka muodostaa x-akselin kanssa kulman θ/2. Peilaus yhden­suuntaisen suoran suhteen vastaa sitä, että tähän lisätään jokin sitä vastaan kohti­suora vektori.

• Liukupeilaus, jolle käytetään merkintää G_c,v,w, missä c on jokin tason piste, v yksikkövektori $\mathbb {R} ^{2}$:ssa ja w v:n kanssa kohti­suorassa oleva vektori, joka ei ole nollavektori. Tämä on yhdistetty kuvaus, jonka muodostavat peilaus c:n ja v:n määräämän suoran kanssa sekä translaatio w:n suunnassa. Toisin sanoen

$G_{c,v,w}=T_{w}\circ F_{c,v},$

eli,

$G_{c,v,w}(p)=w+F_{c,v}(p).\,$

(Pitää myös paikkansa, että

$G_{c,v,w}(p)=F_{c,v}(p+w);\,$

toisin sanoen tulos on sama, jos translaatio ja heijastus suoritetaan päin­vastaisessa järjestyksessä.)

Vaihtoehtoisesti voidaan ensin kertoa orto­gonaalisella matriisilla, jonka determinantti on −1 ja joka vastaa peilausta origon kautta kulkevan suoran suhteen, ja sen jälkeen suorittaa translaatio. Tuloksena on tällöinkin liuku­peilaus, paitsi siinä erikois­tapauksessa, että translaatio on kohti­suorassa peilaus­suoraa vastaan, missä tapauksessa tulos on sama kuin peilattaessa erään toisen, alku­peräisen peilaus­suoran kanssa yhden­suuntaisen suoran suhteen.

Identtinen kuvaus kuvaa jokaisen pisteen itselleen, toisin sanoen I(p) = p kaikille pisteille p. Sekin voidaan käsittää erikois­tapaukseksi sekä translaatiosta että rotaatiosta. Se on ainoa yhtenevyys­kuvaus, joka kuuluu useampaan kuin yhteen edellä luetelluista tyypeistä.

Kaikki tason yhtenevyys­kuvaukset voidaan muodostaa kertomalla orto­gonaalisella matriisilla ja lisäämällä jokin vakio­vektori; jos matriisin determinantti on 1, kyseessä on rotaatio, translaatio tai identtinen kuvaus, ja jos se on −1, on kyseessä liuku­peilaus tai peilaus.

"Satunnainen" yhtenevyys­kuvaus, jota esittää paperi­palan nostaminen pöydältä ja sen palauttaminen sille mieli­valtaiseen kohtaan, on "melkein varmasti" rotaatio tai liuku­peilaus, sillä näillä on kolme vapaus­astetta. Tämä pätee riippumatta todennäköisyysjakaumasta niin kauan kuin θ ja lisätyn vektorin suunta ovat riippumat­tomia ja tasaisesti jakautuneet ja translaatio­vektorin pituudella on jatkuva jakauma. Puhdas translaatio ja puhdas peilaus suoran suhteen ovat erikois­tapauksia, joilla on vain kaksi vapaus­astetta, kun taas identtisellä kuvauksella niitä ei ole yhtään.

Peilausten yhdistelmät

Euklidisessa tasossa on seuraavat mahdollisuudet.

Yhtenevyyskuvaukset peilauksina

• [d  ] Identtinen kuvaus

Kaksi peilausta saman suoran suhteen palauttaa jokaisen pisteen alku­peräiselle paikalleen. Kaikki pisteet ovat kuvauksen kiinto­pisteitä riippumatta siitä, minkä suoran suhteen taso peilataan kahteen kertaan.

• [db] Peilaus

Peilissä oikea ja vasen käsi vaihtuvat, kätisyys vaihtuu, ja samaan tapaan käy tason peilauksessa suoran suhteen. Matemaattisin termein ilmaistuna, topo­loginen orientaatio kääntyy päin­vastaiseksi. Peilaus­suoralla olevat pisteet pysyvät paikoillaan. Peilaus kahden eri suoran suhteen johtaa aina eri tulokseen.

• [dp] Kierto eli rotaatio

Kaksi toisensa leikkaavaa suoraa, joiden suhteen peilaus suoritetaan. Niillä on yksi yhteinen piste, joka pysyy paikoillaan. Kaikki muut pisteet kiertyvät sen ympäri kulman verran, joka on kaksi kertaa peilaus­suorien välinen kulma. Mitkä tahansa kaksi peilaussuoraa, jotka leikkaavat toisensa samassa pisteessä ja joiden välinen kulma on sama, johtavat samaan tulokseen, kunhan peilaukset suoritetaan samassa järjes­tyk­sessä.

• [dd] Yhden­suuntais­siirto eli translaatio

Kaksi peilaus­suoraa, jotka eivät leikkaa toisiaan, ovat yhden­suuntaisia. Jokainen piste siirtyy saman verran, kaksi kertaa peilaus­suorien välisen etäisyyden verran, ja samaan suuntaan. Mikään piste ei pysy paikallaan. Mitkä tahansa kaksi tietyn suuntaista peilaus­suoraa, joilla on sama keskinäinen väli­matka, johtavat samaan tulokseen, kunhan peilaukset suoritetaan samassa järjestyksessä.

• [dq] Liukupeilaus

Kolme peilaus­suoraa. Jos ne kaikki ovat yhden­suuntaisia, voidaan valita yksi suora, jonka suhteen peilattaessa tulos olisi sama. Muussa tapauksessa voidaan löytää kolme suoraa, joista kaksi on yhden­suuntaisia ja kolmas niitä vastaan kohti­suorassa ja jonka suhteen peilattaessa tulos olisi sama. Tuloksena on peilauksen ja peilaus­suoran suuntaisen translaation yhdistelmä. Kiinto­pisteitä ei ole.

Kolme peilausta riittää

Useampien peilaus­suorien lisääminen ei tuo tasossa lisää mahdollisuuksia, sillä ne voidaan aina järjestää uudestaan siten, että osa niistä kumoaa toistensa vaikutukset.

Todistus. Yhtenevyys­kuvauksen määrittää yksi­käsitteisesti kolme pistettä, jotka eivät ole samalla suoralla, ja niiden kuva­pisteet. Oletetaan, että p₁, p₂ ja p₃ kuvautuvat pisteisiin q₁, q₂ ja q₃; tämän aikaan­saamiseksi voidaan seuraavalla tavalla muodostaa kolme peilaus­suoraa. Jos p₁ ja q₁ ovat kaksi eri pistettä, valitaan peilaus­suoraksi niiden välisen janan keskinormaali. Nyt p₁ kuvautuu pisteeseen q₁ ja molemmat muut peilaus­suorat voidaan valita niin, että ne kulkevat q₁:n kautta ja pitävät sen paikoillaan. Käytetään pisteiden p₂ ja p₃ kuva­pisteille tässä peilauksessa merkintöjä p₂′ ja p₃′.

Jos q₂ ei ole sama kuin p₂′, valitaan pisteessä q₁ olevan kulman puolittaja uudeksi peilaussuoraksi. Kun p₁ ja p₂ nyt ovat paikoillaan, p₃ on pisteessä p₃′′; ja jos se ei ole paikoillaan, kolmas peilaus pisteiden q₁ ja q₂ kautta kulkevan suoran suhteen kuvaa sen pisteeseen q₃. Täten jokainen yhtenevyys­kuvaus voidaan muodostaa yhdistämällä enintään kolmesta peilauksesta. mot.

Tunnistus

Mikä näistä yhtenevyys­kuvausten tyypeistä kulloinkin on kyseessä, voidaan seuraavan taulukon mukaisesti tunnistaa sen perusteella, säilyttääkö se kätisyyden vai vaihtaako se sen, ja onko sillä ainakin yksi kiinto­piste. (Identtistä kuvausta ei oteta huomioon.)

		Säilyykö kätisyys?
		Kyllä	Ei
Kiintopiste?	Kyllä	Rotaatio	Peilaus
	Ei	Translaatio	Liukupeilaus

Ryhmän rakenne

Tason yhtenevyys­kuvausten ryhmää sanotaan euklidiseksi ryhmäksi. Yhtenevyys­kuvaukset, jotka muodostetaan parittomasta määrästä peilauksia - itse peilaus sekä liukupeilaus - vaihtavat aina keskenään vasemman ja oikean. Yhtenevyys­kuvauksella sanotaan olevan parillinen tai pariton pariteetti riippuen siitä, voidaanko muodostaa yhdistämällä parillisesta vai parittomasta määrästä peilauksia. Parilliset yhtenevyys­kuvaukset - identtinen kuvaus sekä translaatio ja rotaatio, eivät koskaan tee niin. Ne voidaan käsittää tason jäykiksi liikkeiksi, ja ne muodostavat tämän ryhmän normaalin aliryhmän. Sen enempää koko euklidinen ryhmä kuin tämä ali­ryhmäkään eivät ole Abelin ryhmiä; esimerkiksi jos taso peilataan kahden yhdensuuntaisen suoran suhteen eri järjestyksissä, tuloksena on kaksi translaatiota päin­vastaisiin suuntiin.

Todistus: Identtinen kuvaus on yhtenevyys­kuvaus; mikään ei muutu, joten etäisyydetkään eivät muutu. Ja jos yksi kuvaus ei muuta etäisyyksiä, ei sitä voi muuttaa kaksi, kolme tai useampikaan tällainen kuvaus yhdistettynä; näin ollen yhtenevyys­kuvausten yhdistetty kuvaus on jälleen yhdistetty kuvaus, ja yhtenevyys­kuvausten joukko on suljettu niiden yhdistämisen suhteen. Identtinen kuvaus on myös identiteetti kuvausten yhdistämisessä, ja yhdistäminen on liitännäinen; sen vuoksi yhtenevyys­kuvaukset muodostavat puoliryhmän. Ryhmässä jokaisella alkiolla on myös käänteis­alkio. Peilauksen käänteis­kuvaus on sama peilaus itse, eli peilaukset ovat involuutioita. Ja koska jokainen yhtenevyys­kuvaus voidaan esittää peilauksista yhdistettynä kuvauksena, sen käänteis­kuvaus saadaan suorittamalla nämä peilaukset päin­vastaisessa järjestyksessä. On huomattava, että jos kaksi perättäistä peilausta saman suhteen, jotka kumoavat toisensa, jätetään huomiotta, suoritettavien peilausten lukumäärä pienenee parillisen luvun verran, mikä säilyttää yhdistetyn kuvauksen pariteetin, jota paitsi identtisellä kuvauksella on parillinen pariteetti. Tämän vuoksi kaikki yhtenevyyskuvaukset muodostavat ryhmän, ja parilliset yhtenevyys­kuvaukset muodostavat sen aliryhmän. (Parittomien yhtenevyys­kuvausten joukkoon identtinen kuvaus ei kuulu, joten ne eivät muodosta ali­ryhmää.) Tämä aliryhmä on normaali aliryhmä, sillä jos kahden parittoman yhtenevyys­kuvauksen väliin lisätään parillinen yhtenevyys­kuvaus, tuloksena on parillinen yhtenevyys­kuvaus. mot.

Koska parillisten kuvausten aliryhmä on normaali, se on homeomorfismin ydin, ja sen tekijäryhmä on iso­morfinen ryhmän kanssa, johon kuuluvat yksi peilaus ja identtinen kuvaus.

Kuvausten yhdistäminen

Yhtenevyys­kuvausten yhdistäminen muuttaa niiden tyyppejä usein eri tavoin. Identtistä kuvausta voidaan pitää joko kahden peilauksen yhdistettynä kuvauksena tai ei yhdenkään; kummassakaan tapauksessa se ei muuta muiden kuvausten tyyppiä. Kahden peilauksen yhdistäminen antaa tulokseksi trans­laation tai rotaation, tai erikois­tapauksessa identtisen kuvauksen, joka kuuluu triviaalilla tavalla molempiin ryhmiin. Peilaus yhdistettynä jompaan­kumpaan näistä voi palautua yhdeksi peilaukseksi, mutta ellei niin tapahdu, tuloksena on ainoa kolmesta peilauksesta yhdistetty kuvaus, liukupeilaus. Kahden translaation yhdistäminen johtaa aina kuvaukseen, joka itsekin on translaatio. Moni­mutkaisempia ovat tapaukset, joissa ainakin toinen kuvauksista on rotaatio. Tiedämme, että rotaation yhdistäminen joko toiseen rotaatioon tai translaatioon on aina parillinen yhtenevyys­kuvaus. Translaation ja rotaation yhdistettynä kuvauksena saadaan toinen rotaatio, jossa kiertokulma on sama mutta kiinto­piste toinen. Sen sijaan kahden rotaation yhdistetty kuvaus voi olla joko rotaatio tai trans­laatio. Usein sanotaan, että kahden rotaation yhdistetty kuvaus johtaa rotaatioon, ja Euler todisti tätä koskevan teoreeman kolmi­ulotteisessa avaruudessa; tämä kuitenkin pätee vain rotaatioille, joilla on yhteinen kiinto­piste.

Translaatioiden, rotaatioiden ja ortogonaaliset aliryhmät

Edellä olevan perusteella voidaan yhtenevyys­kuvausten ryhmälle muodostaa uusia ali­ryhmiä. Erään sellaisen muodostavat kaikki trans­laatiot, ja myös kaikki rotaatiot saman pisteen ympäri muodostavat aina ali­ryhmän. Molemmat ovat parillisen ali­ryhmän ali­ryhmiä, ja trans­laatioiden ali­ryhmä on sen normaali ali­ryhmä. Koska trans­laatiot ovat normaali al­iryhmä, ne voidaan sulkea pois, jolloin jäljelle jää sellaisten yhtenevyys­kuvausten aliryhmä, joilla on kiinto­piste, ortogonaalinen ryhmä.

Translaatioiden ja peilausten yhdistetyt kuvaukset

Todistus. Jos kahdella rotaatiolla on yhteinen kiinteä piste, ne kaksi suoraa, joiden suhteen suoritetta­vista peilauksista yhdistämällä jälkimm­äinen saadaan, voidaan valita siten, että niistä ensim­mäinen on sama kuin ensim­mäisen rotaation jälkim­mäisen peilauksen peilaus­suora. Täten neljästä peilauksesta kaksi keskim­mäistä kumoavat toisensa ja jäljelle jäävät vain ensim­mäinen rotaation ensim­mäinen ja jälkim­mäisen rotaation jälkim­mäinen peilaus. Niinpä kahden sellaisen rotaation yhdistetty kuvaus, joilla on yhteinen kiinteä piste, on rotaatio, jolla on sama kiinteä piste niiden kumman­kin kanssa ja jonka kierto­kulma on niiden kierto­kulmien summa.

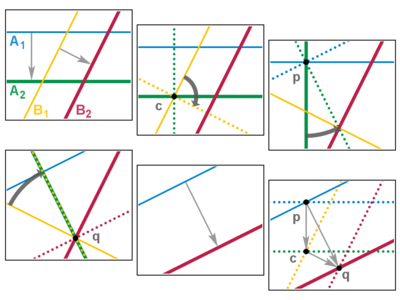
Jos kaksi trans­laatiota ovat yhden­suuntaisia, ne kaksi suoraa, joiden suhteen suoritetta­vista peilauksista yhdistämällä jälkim­mäinen saadaan, voidaan valita siten, että niistä ensim­mäinen on sama kuin ensim­mäisen trans­laation jälkim­mäisen peilauksen peilaus­suora. Täten neljästä peilauksesta kaksi keskim­mäistä kumoavat toisensa ja jäljelle jäävät vain ensim­mäisen trans­laation ensim­mäinen ja jälkim­mäisen trans­laation jälkim­mäinen peilaus. Niinpä kahden yhden­suuntaisen trans­laation yhdis­tetty kuvaus on niiden kanssa yhden­suuntainen trans­laatio, jossa siirretty matka on niissä kummassa­kin siirrytyn matkan summa. Jos taas translaatiot eivät ole yhden­suuntaiset ja peilaus­suorat ovat A₁, A₂ (ensim­mäinen trans­laatio) sekä B₁, B₂ (jälkim­mäinen trans­laatio), leikkaavat A₂ ja B₁ jossakin. Merkitään niiden leikkauspistettä c:llä, ja yhdistele­mällä peilaukset toisin saadaan kahdesta keskim­mäisestä yhdistä­mällä rotaatio pisteen c ympäri. Sama rotaatio voidaan saada myös kiertä­mällä näitä kahta peilaus­suoraa 90° pisteen c, jolloin niiden välinen kulma pysyy ennallaan. Nyt A₁ ja A₂′ leikkaavat toisensa 90°:n kulmassa jossakin pisteessä, jolle käytetään merkintää p, ja samoin B₁′ ja B₂ leikkaavat toisensa jossakin pisteessä q. Yhdistellään peilaukset jälleen uudestaan siten, että ensimmäistä paria kierretään pisteen p ympäri siten, että B₂″ kulkee q:n kautta ja vastaavasti toista paria pisteen q ympäri siten, että A₁″ kulkee p:n kautta. Nyt kaksi keskimmäistä peilaussuoraa yhtyvät ja peilaukset kumoavat toisensa, kun taas ensimmäinen ja viimeinen ovat edelleen yhdensuuntaiset. Näin ollen kahden translaation yhdistetty kuvaus on trans­laatio silloinkin, kun ne eivät ole yhden­suuntaiset. Lisäksi ne kolme pistettä, joiden ympäri peilaus­suoria kierrettiin, muodostavat kolmion, joka esittää vektorien yhteen­laskua: 2(p c) + 2(c q) = 2(p q). mot.

Konstruointi aliryhmän avulla

Aliryhmän rakenne tarjoaa toisen keinon, jolla mikä tahansa yhtenevyys­kuvaus voidaan muodostaa:

Valitaan kiinteä piste ja jokin sen kautta kulkeva suora peilaussuoraksi

1. Jos yhtenevyys­kuvaus on pariton, suoritetaan peilaus, muussa tapauksessa ei.
2. Jos on tarpeen, suoritetaan rotaatio (kierto) valitun pisteen ympäri
3. Jos on tarpeen, suoritetaan translaatio (yhdensuuntais­siirto)

Tämä toimii, koska translaatiot muodostavat kaikkien yhtenevyys­kuvausten normaalin ali­ryhmän, jonka tekijäryhmänä on ortogonaalinen ryhmä, ja rotaatiot annetun pisteen ympäri muodostavat orto­gonaalisen ryhmän normaalin ali­ryhmän, jonka tekijä­ryhmänä on yksi peilaus.

Diskreetit aliryhmät

Säännöllisen viisikulmion symmetrioiden diedriryhmä

Tähän saakka käsitellyt ali­ryhmät ovat kaikki olleet, paitsi äärettömiä, myös jatkuvia, Lien ryhmiä. Jokainen ali­ryhmä, johon kuuluu ainakin yksi ei-triviaali translaatio, on ääretön, mutta orto­gonaalisella ryhmällä on myös äärellisiä ali­ryhmiä. Esimerkiksi säännöllisen viisikulmion symmetrioita ovat rotaatiot sellaisten kulmien verran, jotka ovat 72°:n (360° / 5) moni­kertoja sekä peilaukset sen sivujen keskinormaalien suhteen. Nämä muodostavat ryhmän D₅, jossa on 10 alkiota. Sillä on aliryhmä, C₅, johon kuuluu viisi rotaatiota mutta eivät peilaukset. Nämä ryhmät kuuluvat kahteen perheeseen, D_n ja C_n, jotka voidaan muodostaa jokaiselle kokonais­luvulle n > 1. Yhdessä nämä perheet muodostavat kaksi­ulotteiset pisteryhmät.

Translaatio ei itsensä kanssa yhdistettynä johda identtiseen kuvaukseen, suoritet­tiinpa se kuinka monta kertaa tahansa, mutta erään yhtenevyys­kuvausten ali­ryhmän muodostavat kaikki translaatiot, jotka saadaan suorittamalla annettu translaatio tai sen käänteiskuvaus mieli­valtaisen monta kertaa. Tämä ryhmä on iso­morfinen kokonaislukujen ryhmän kanssa. Ali­ryhmiä saadaan myös niistä kuvauksista, jotka saadaan toistamalla kahta trans­laatiota, kumpaakin toisistaan riippumatta mieli­valtaisen monta kertaa. Nämä muodostavat tason hilaryhmän.

Näitä kahden­laisia diskreettejä ryhmiä voidaan myös yhdistellä. Diskreetit rotaatiot ja peilaukset annetun pisteen ympäri ja diskreetit trans­laatiot yhdessä muodostavat niin sanottuja friisi­ryhmiä (engl. frieze group) ja tapetti­ryhmiä (engl. wallpaper group). Mielenkiintoista kylläkin, vain pieni osa ryhmistä, jotka liittyvät kiinteisiin pisteisiin, ovat yhteen­sopivia diskreettien trans­laatioiden kanssa. Itse asiassa tämä yhteen­sopivuus asettaa siinä määrin rajoittavia ehtoja, aina iso­morfis­meja myöten, että on olemassa vain seitsemän erilaista friisi­ryhmää ja 17 erilaista tapetti­ryhmää. Esimerkiksi viisikulmion symmetriat, D₅, eivät ole yhteen­sopivia trans­laatioiden diskreetin ryhmän kanssa. (Missä tahansa useampi­ulotteisessa avaruudessa on niin ikään vain äärellinen määrä tällaisia kristallo­grafisia ryhmiä, mutta niiden luku­määrä kasvaa nopeasti; esimerkiksi kolmessa ulottuvuudessa on 320 ja neljässä ulottuvuudessa 4783 ryhmää.)

Yhtenevyyskuvaukset kompleksitasolla

Jos tason pisteitä käsitellään kompleksilukuina, tason yhtenevyys­kuvaukset ovat joko muotoa

${\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega z\end{array}}$

tai

${\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega {\overline {z}}{\mbox{,}}\end{array}}$

missä a ja ω ovat eräitä kompleksilukuja ja |ω| = 1. Tämä on helppo todistaa: jos a = f(0) ja $\omega$ = f(1) − f(0) ja jos määritellään

${\begin{array}{rccc}g\colon &\mathbb {C} &\longrightarrow &\mathbb {C} \\&z&\mapsto &{\frac {f(z)-a}{\omega }}{\mbox{,}}\end{array}}$

on g yhtenevyyskuvaus, g(0) = 0, ja g(1) = 1. Nähdään helposti, että g on joko identtinen kuvaus tai kompleksikonjugaatti, ja todistettava lause seuraa tästä sekä siitä, että f(z) = a + ωg(z).

Tämä liittyy yksinkertaisella tavalla edellä esitettyyn tason yhtenevyys­kuvausten luokitteluun sillä

• tyyppiä z → a + z olevat funktiot ovat trans­laatiota;
• tyyppiä z → $\omega$z olevat funktiot ovat rotaatiota (kun |ω| = 1);
• kompleksikonjugaation ottaminen on peilaus.

Lähteet

• Tason yhtenevyyskuvauksista

Kirjallisuutta

• Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6