Lambertin oikeapintainen tasoprojektio

Lambertin oikeapintainen tasoprojektio on eräs kuvaus pallopinnalta tason kiekolle eli ympyräviivan sisäpuolelle jäävälle alueelle. Siinä jokainen pallopinnan alue kuvautuu tasoalueelle, jonka pinta-ala on yhtä suuri kuin alkuperäisen alueen, mutta kulmien suuruudet muuttuvat. Kuvaus on nimetty sveitsiläisen matemaatikko Johann Heinrich Lambertin mukaan, joka esitti sen vuonna 1772.[1]
Lambertin oikeapintaista tasoprojektiota käytetään kartografiassa karttaprojektiona. Esimerkiksi Yhdysvalloissa National Atlas of the United States käytti sitä Map Maker -sovelluksessa[2], ja Euroopan ympäristövirasto suosittelee sen käyttöä tilastollista aineistoa kuvaavissa Euroopan kartoissa.[3] Sitä käytetään myös tieteellisissä yhteyksissä kuten geologiassa suorien suuntien kuvaamiseen kolmiulotteisessa avaruudessa. Tähän tarkoitukseen käytetään apuna erityisellä ruudukolla varustettua paperia, joka tunnetaan nimellä Schmidtin verkko.[4]
Matemaattinen määritelmä
[muokkaa | muokkaa wikitekstiä]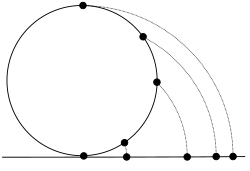
Lambertin oikeapintainen tasoprojektio määritellään ajattelemalla, että taso sivuaa pallopintaa jossakin pisteessä S. Olkoon P mielivaltainen tason piste, ei kuitenkaan S:n antipodipiste. Olkoon d pisteiden S ja P välinen suora etäisyys kolmiulotteisessa avaruudessa (ei siis pallopintaa pitkin mitattuna). Tällöin piste P kuvautuu tasolle pisteeseen P′, jonka etäisyys sivuamispisteestä S on d.
Täsmällisemmin sanottuna on olemassa yksikäsitteinen ympyrä S, joka kulkee pisteen P kautta ja on kohtisuorassa tasoa vastaan. Se leikkaa tason kahdessa pisteessä, ja merkitään P′:llä sitä niistä, joka on lähempänä P:tä. Piste P kuvautuu siihen. S:n antipodipisteellä ei ole yksikäsitteistä kuvauspistettä, koska sitä tällä tavoin vastaava ympyrä ei ole yksikäsitteinen. Piste S itse kuvautuu itselleen; sitä vastaavan "ympyrän" säde on nolla.[5]
Koordinaatit
[muokkaa | muokkaa wikitekstiä]Jos sivuamispiste S sijaitsee leveyspiirillä ja pituuspiirillä , maan pinnan piste, jonka maantieteellinen leveys on ja pituus , kuvautuu tasolle pisteeseen, jonka karteesiset koordinaatit (x, y) ovat:
missä tekijä k' on
- .[6]
Tekijä k' on verrannollinen kartan paikalliseen mittakaavaan kussakin pisteessä kyseisen pisteen ja sivuamispisteen kautta kulkevaa suoraa vastaan kohtisuorassa suunnassa.[7]
Erikoistapauksia
[muokkaa | muokkaa wikitekstiä]Jos sivuamispiste S on pohjoisnavalla (φ1 = 90°), on ja . Tällöin k:n lauseke yksinkertaistuu muotoon
ja koordinaattien lausekkeet muotoon
Leveyspiiri kuvautuu tällöin ympyräksi, jonka keskipiste on kartan pohjoisnavalla ja jonka säde on
- .
Jos taas sivuamispiste S on päiväntasaajalla (φ1 = 0°), on ja Tällöin k':n lauseke yksinkertaistuu muotoon
ja koordinaattien lausekkeet muotoon
Ominaisuuksia
[muokkaa | muokkaa wikitekstiä]Seuraavassa oletetaan, että vaakasuora taso sivuaa origokeskeistä yksikköpalloa pisteessä (0, 0, -1). Tällöin Lambertin oikeapintainen tasoprojektio matemaattisena kuvauksena on määritelty muissa yksikköpallon pinnan pisteissä paitsi pisteessä (0, 0, 1). Muut pallopinnan pisteet se kuvaa origokeskeiselle avoimelle kiekolle, jonka säde on 2. Pallon päiväntasaajan eli ne pisteet, joissa z = 0 se kuvaa origokeskeiselle ympyrälle, jonka säde on . Päiväntasaajatason alapuolella olevat pisteet, joissa z < 0, kuvautuvat tämän ympyrän sisäpuolelle, yläpuolella olevat sen ulkopuolelle.
Projektio on bijektio pallopinnalta, josta on poistettu piste (0,0,1) avoimelle kiekolle, jonka säde on 2. Se on myös diffeomorfismi, toisin sanoen äärettömän monta kertaa differentioituva molemmissa suunnissa. Siinä kuvajoukon pinta-ala on aina yhtä suuri kuin lähtöjoukon, mikä voidaan osoittaa laskemalla pinta-alkion ala pallolla, kun sitä parametrisoi projektion käänteiskuvaus. Karteesisissa koordinaateissa se on
Tämä merkitsee, että pallopinnalla olevan alueen pinta-alan määrittämiseksi riittää mitata sitä tason kiekolla vastaavan alueen pinta-ala.
Toisaalta projektiossa eivät pallopinnan käyrien väliset kulmat säily. Missään kuvauksessa joltakin pallon alueelta jollekin tason alueelle eivät säilykään sekä pinta-alat että kulmat. (Jos molemmat säilyisivät, kyseessä olisi lokaali isometria, jossa Gaussin kaarevuus säilyisi, mikä ei kuitenkaan ole mahdollista, koska pallopinnalla ja tasolla on eri suuri kaarevuus.) Se seikka, että tasokuviot eivät voi täydellisesti vastata pallopinnan alueita, onkin kartografian perustava ongelma.
Tästä seuraa, että pallopinnan alueet saattavat kuvautua tasolle suuresti vääristyneinä. Lambertin oikeapintaisessa tasoprojektiossa tämä vääristymä on erityisen suuri kaukana projektion sivuamispisteestä. Yleensä tätä projektiota käytetäänkin vain enintään pallonpuoliskon laajuista aluetta esittävissä kartoissa. Koko maapallo voidaan kuitenkin kuvata kahdella erillisellä Lambertin oikeapintaisen tasoprojektion mukaisella kartalla, joiden sivuamispisteet ovat toistensa antipodissa.
Sovelluksia
[muokkaa | muokkaa wikitekstiä]Lambertin tasoprojektio tarkoitettiin alun perin oikeapintaiseksi karttaprojektioksi. Nykyisin sitä käytetään muillakin aloilla kuten geologiassa suuntia kuvaavan aineiston kuvaamiseen seuraavasti.
Jokaista suuntaa kolmiulotteisessa avaruudessa vastaa jokin origon kautta kulkeva suora. Kaikkien sellaisten suorien joukko on itsessään avaruus, jota matematiikassa sanotaan reaaliseksi projektiiviseksi tasoksi. Jokainen origon kautta kulkeva suora leikkaa yksikkökiekon kahdessa pisteessä, joista toinen on alemmalla pallonpuoliskolla . Poikkeuksena ovat vaakasuorat viivat, joiden leikkauspisteet sijaitsevat kahdessa vastakkaisessa pisteessä ekvaattorilla, . Molemmat toistensa antipodissa olevat pisteet vastaavat samaa suoraa. Täten suunnat kolmiulotteisessa avaruudessa vastaavat lähes täysin alemman pallonpuoliskon pisteitä. Tämä pallonpuolisko voidaan sitten Lambertin oikeapintaisella projektiolla kuvata kiekolle, jonka säde on .
Niinpä Lambertin oikeapintaisella projektiolla voidaan jokaista suuntaa vastaamaan asettaa tason piste. Projektion oikeapintaisuuden vuoksi suuntien muodostamassa avaruudessa eli reaalisella projektiivisella tasolla määritellyt funktiot voidaan integroida integroimalla funktio vastaavan tasoalueen yli. Tämä on käyttökelpoista eri suuntia koskevan aineiston käsittelyssä.[5]
Eivät ainoastaan suorat, vaan myös origon kautta kulkevat tasot voidaan kuvata Lambertin oikeakulmaisella projektiolla. Tason ja pallonpuoliskon leikkaus on ympyränkaari, jota sanotaan tason uraksi, ja se kuvautuu yksikkökiekkoon käyräksi, joka yleensä ei ole ympyränkaari. Voidaan kuvata tätä käyrää, tai vaihtoehtoisesti taso voidaan korvata sen kohtisuorasti leikkaavalla suoralla, jota sanotaan sen navaksi ja kuvata tason sijasta tätä käyrää. Jos useita tasoja on kuvattava yhdessä, on yksinkertaisempaa käsitellä napoja urien sijasta.
Rakennegeologian tutkijat käyttävät Lambertin oikeapintaista tasoprojektiota kuvaamaan muun muassa mineraalien kiderakenteen erisuuntaisia akseleita ja pintoja, lineaatioita ja foliaatioita eri kivilajeissa. Tässä yhteydessä projektiota kutsutaan oikeapintaiseksi hemisfääriseksi projektioksi. Erikseen on olemassa myös oikeakulmainen hemisfäärinen projektio, jonka määrittelee stereografinen projektio.[5]
Edellä on oletettu, että suunnat kuvataan alemmalle pallonpuoliskolle, , mutta yhtä hyvin ne voidaan kuvata myös ylemmälle pallonpuoliskolle , kuten toisinaan tehdäänkin.[5] Itse asiassa mitä tahansa pallopinnan puoliskoa voitaisiin käyttää esittämään origon kautta kulkevia suoria kolmiulotteisessa avaruudessa.
Lähteet
[muokkaa | muokkaa wikitekstiä]- Manfredo P. Do Carmo: Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall, 1976. ISBN 0-13-212589-7
- Bruce E. Hobbs, Winthrop D. Means, Paul F. Means: An outline of structural geology. New York. Määritä julkaisija! 0-471-40156-0
- Michael Spivak: A comprehensive introduction to differential geometry. Houston, Texas: Publish or Perish, 1999. ISBN 0-914098-70-5
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ Lambert Azimuthal Equal Area Karen Mulchahy, City University of New York. Viitattu 30.12.2014.
- ↑ Map Projections: From Spherical Earth to Flat Map 29.4.2008. United Sates department of the Interior. Arkistoitu 7.5.2009. Viitattu 30.12.2014.
- ↑ Short Proceedings of the 1st European Workshop on Reference Grids 27.-29.10.2003. Euroopan ympäristövirasto. Viitattu 30.12.2014.
- ↑ John G. Ramsay: Folding and fracturing of rocks. New York: McGraw-Hill, 1967.
- ↑ a b c d Graham D. Borradaile: Statistics of Earth science data. Berliini: Springer-Verlag, 2003. ISBN 3-540-43603-0
- ↑ Lambert Azimuthal Equal-Area Projection MathWorld. Viitattu 30.12.2014.
- ↑ John P. Snyder: ”Lambert Azimutal Equal-area Projection”, Map Projections - A Working Manual, s. 185. Washington D. C.: United States Government Print Office, 1987. Teoksen verkkoversio. (Arkistoitu – Internet Archive)

















![{\displaystyle x=k'\cos ]]{\phi })\sin {(\lambda -\lambda _{0})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61dfa4dccc531f4cc4df7d1c561a0b5a8ef6f325)






