Homografia

Homografia eli projektiivinen muunnos on projek­tiivisessa geo­metriassa projek­tiivisten avaruuksien välinen isomorfismi, jonka indusoivat niiden vektori­avaruuksien välinen isomorfismi, josta ne on johdettu. Se on bijektio, jossa suorat kuvautuvat suoriksi ja näin ollen kollineaatio. Joissakin projek­tiivisissa avaruuksissa voi olla myös kolline­aatioita, jotka eivät ole homo­grafioita, mutta projek­tiivisen geo­metrian perus­lauseen mukaan vähintään kaksi­ulotteisissa reaali­sissa projek­tiivisissa avaruuksissa jokainen kolli­neaatio on samalla homo­grafia. Joskus homo­grafioista käytetään myös nimityksiä projektivi­teetti tai projek­tiivinen kolline­aatio.

Historiallisesti homografiat samoin kuin projek­tiiviset avaruudetkin on otettu käyttöön perspektiiviopin ja euklidisen geo­metrian projektioiden yhteydessä. Tähän viittaa myös nimitys homo­grafia, joka etymo­logisesti merkitsee suunnilleen "saman­laista piirtämistä". Myöhemmin 1800-luvun lopulla otettiin käyttöön muodolliset projek­tiivisten avaruuksien määritelmät, joiden mukaan nämä avaruudet erosivat euklidisista ja affiineista avaruuksista siinä, että niihin oli lisätty äärettö­myydessä olevia pisteitä. Näiden abstraktien kon­struk­ti­oi­den myötä otettiin käyttöön termi "projek­tiivinen muunnos". Nämä kon­struk­tiot jakautuvat kahteen luokkaan, jotka on osoitettu ekvi­valenteiksi. Projek­tiivinen avaruus voidaan konstruoida suorien joukkona jonkin kunnan yli muodostetussa vektori­avaruudessa; tähän kon­struk­tioon perustuen voidaan määritellä projektiiviset koordinaatit, ja homo­grafioiden tutkimukseen voidaan soveltaa lineaarialgebraa. Vaihtoehtoinen lähestymistapa perustuu siihen, että projektiivinen avaruus määritellään aksiooma­ryhmän avulla, jossa ei ekspli­siittisesti viitata mihinkään kuntaan (insidenssigeometria). Tältä pohjalta kollineaatio on helpompi määritellä kuin homo­grafia, ja homo­grafia määritellään tietyntyyppisenä kolline­aationa, minkä vuoksi sitä sanotaankin myös "projek­tiiviseksi kolline­aatioksi".

Yksin­kertaisuuden vuoksi jäljempänä tässä artikkelissa oletetaan, paitsi milloin toisin mainitaan, että projek­tiiviset avaruudet on määritelty jonkin (kommuta­tiivisen) kunnan yli. Oletetaan myös, että Pappuksen kuusikulmiolause ja Desarguesin lause pätevät. Suuri osa tuloksista kuitenkin pätee tai voidaan yleistää myös sellaisiin projek­tiivisiin geo­metrioihin, joissa nämä lauseet eivät päde.

Geometrinen tausta

Pisteet A, B, C, D ja A', B', C', D' liittyvät toiseensa perspektiivisesti, projektiivisella muunnoksella

Historiallisesti homografian käsite on otettu käyttöön visuaalisen perspektiivin ymmärtämiseksi, selittämiseksi ja tutkimiseksi ja erityisesti sen selvittämiseksi, millä tavoin kaksi tasokuviota näyttävät erilaisilta eri näkökulmista katsottuina.

Kolmiulotteisessa euklidisessa avaruudessa keskeisprojektio pisteestä O (keskuksesta) tasolle P, johon piste O ei sisälly, on kuvaus, jolla piste A kuvataan tason P ja suoran OA leikkaus­pisteeseen, jos sellainen on olemassa. Projektio ei ole määritelty, jos piste A sijaitsee O:n kautta kulkevalla, P:n kanssa yhden­suuntaisella tasolla. Projek­tiivisen avaruuden käsite otettiin alun perin käyttöön euklidisen avaruuden laajennuksena lisäämällä siihen äärettö­myydessä olevat pisteet, jotta projektio voidaan määritellä kaikille muille pisteille paitsi O:lle.

Jos on annettu toinen taso Q, johon piste O ei sisälly, Q:n rajoittumaa edellä mainitussa projektiossa sanotaan per­spek­tivi­teetiksi.

Näin määriteltynä per­spek­tivi­teetti on vain osittaisfunktio, mutta projek­tiivi­siin avaruuksiin laajennettuna siitä tulee bijektio. Siksi tämä käsite määritellään tavallisimmin projek­tiivi­sille avaruuksille. Käsite voidaan seuraavasti myös helposti yleistää jokaiselle projektiiviselle avaruudelle, olipa sen ulottuvuus mikä tahansa tai olipa se muodostettu minkä tahansa kunnan yli: jos on annettu kaksi n-ulotteista projek­tiivista avaruutta P ja Q, per­spek­tivi­teetti on bijektio P:stä Q:lle, joka saadaan upottamalla P ja Q n+1 -ulotteiseen projek­tiivi­seen avaruuteen R ja rajoittamalla P:hen jokin keskeis­projektio Q:hun.

Jos f on perspektiviteetti P:stä Q:hun ja g perspektiiviteetti Q:sta P:hen, niin yhdistetty kuvaus g°f on homografia P:stä itseensä. Sitä sanotaan keskeiskollineaatioksi, kun P on vähintään kaksiulotteinen.

Alun perin homografia määriteltiin yhdistelmäksi äärellisestä määrästä perspektivi­teettejä. Projektiivisen geometrian peruslauseesta seuraa, että tämä määritelmä on yhtäpitävä johdannossa esitetyn ja jäljempänä yksityis­kohtaisemmin käsitellyn algebrallisemman määritelmän kanssa.

Määritelmä ja esitys homogeenisilla koordinaateilla

n-ulotteinen projektiivinen avaruus kunnan K yli voidaan määritellä suorien joukoksi n+1 -ulotteisessa vektoriavaruudessa, jonka kerroinkunta on K. Jos V:n kanta on kiinnitetty, jokainen V:n piste voidaan esittää Kⁿ⁺¹:n pisteenä $(x_{0},\ldots ,x_{n})$. Koska P(V):n piste on V:n suora, se voidaan esittää minkä tahansa tämän suoran pisteen koordi­naateilla, origoa lukuun ottamatta, ja näitä sanotaan projek­tiivisen avaruuden pisteen homo­geenisiksi koordi­naateiksi.

Jos on annettu kaksi yhtä moni­ulotteista projek­tiivista P(V) ja P(W), homo­grafia on vektori­avaruuksien välisen isomorfismin $f:V\rightarrow W$ indusoima kuvaus P('V):sta P(W):hen. Koska f on lineaarinen, tällainen iso­morfismi indusoi bijektion P('V):sta P(W):hen. Kaksi isomorfismia, f ja g, indusoivat saman homo­grafian, jos ja vain jos K:ssa on alkio a, joka ei ole nolla-alkio ja jolle g = af.

Tämä voidaan esittää homo­geenisilla koordi­naateilla seuraavasti: Homografia f voidaan määritellä kääntyvällä n+1 × n+1 -matriisilla [a_i,j], jota sanotaan homografiamatriisiksi. Pisteen x homo­geenisten koordi­naattien $[x_{0}:\cdots :x_{n}]$ ja sen kuva­pisteen y = f(x) koordi­naattien välillä on relaatio

${\begin{aligned}y_{0}&=a_{0,0}x_{0}+\dots +a_{0,n}x_{n}\\&\vdots \\y_{n}&=a_{n,0}x_{0}+\dots +a_{n,n}x_{n}.\end{aligned}}$

Kun projek­tiiviset avaruudet on määritelty lisäämällä affiineihin avaruuksiin äärettö­myydessä olevia pisteitä (projektiivinen täydennys), nämä kaavat voidaan esittää affiineilla koordi­naateilla seuraavasti:

${\begin{aligned}y_{1}&={\frac {a_{1,0}+a_{1,1}x_{1}+\dots +a_{1,n}x_{n}}{a_{0,0}+a_{0,1}x_{1}+\dots +a_{0,n}x_{n}}}\\&\vdots \\y_{n}&={\frac {a_{n,0}+a_{n,1}x_{1}+\dots +a_{n,n}x_{n}}{a_{0,0}+a_{0,1}x_{1}+\dots +a_{0,n}x_{n}}}\end{aligned}}$

mikä yleistää seuraavassa osiossa käsiteltävää homo­grafista funktiota. Tämä määrittelee vain osittaisfunktion affiinen avaruuksien välille, sillä funktiota ei ole määritelty hypertasolla, jossa nimittäjä on nolla.

Projektiivisen suoran homografiat

Kompleksitason homo­grafioissa toisensa kohti­suorasti leikkaavien ympyröiden kuvat leikkaavat niin ikään toisensa kohti­suorasti

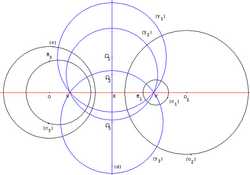
Projektiivinen suora kunnan K yli voidaan samastaa sen joukon kanssa, joka saadaan lisäämällä K:hon yksi piste, jota sanotaan äärettö­myydessä olevaksi pisteeksi ja merkitään ∞. Kun projek­tiiviset suorat määritellään näin, homo­grafioita ovat kuvaukset

$z\mapsto {\frac {az+b}{cz+d}},{\text{ where }}ad-bc\neq 0,$

joita snotaan homo­grafisiksi funktioiksi tai lineaari­siksi fraktio­naali­siksi muunnoksiksi.

Projektiivinen suora kompleksilukujen kunnan yli tunnetaan Riemannin pallona, ja sen homogra­fioita sanotaan Möbius-kuvauksiksi. Ne ovatkin ainoat Riemannin pallon bijektiot itselleen, joissa orientaatio säilyy ja jotka ovat konformi­kuvauksia.

Kollineaatioiden teoriassa projektiiviset suorat ovat erikois­asemassa yksi­ulotteisuutensa vuoksi. Kun suoraa pidetään itsenäisenä projek­tiivisena avaruutena, jokainen sen pisteiden permutaatio on kollineaatio, sillä mitkä tahansa pisteet ovat samalla suoralla. Jos projek­tiivinen suora kuitenkin upotetaan useampi­ulotteiseen projektiivisen avaruuteen, tätä avaruuden geometrista rakennetta voidaan käyttää muodostamaan suoralle geometrinen rakenne. Synteettisessä geometriassa käsitellään sen vuoksi vain niitä projek­tiivisen suoran homografioita ja kolline­aatioita, jotka saadaan tämän useampi­ulotteisen avaruuden homo­grafioista ja kollineaatioista. Tällöin projektiivisen geometrian peruslause pätee myös yksi­ulotteisessa tapauksessa. Projek­tiivisen suoran homo­grafia voidaan yhtä­pitävästi määritellä myös kuvaukseksi, jossa kaksoissuhde säilyy.

Keskeiskollineaatiot

Pisteet A, B, C, D ja A', B', C', D' liittyvät toisiinsa useammalla keskeis­kollineaatiolla, jotka saadaan täysin määritetyiksi valitsemalla kiinteiden pisteiden muodostama suora L, joka kulkee suorien ABCD ja A'B'C'D' leikkaus­pisteen kanssa. Olkoon O suorien AA', BB', CC' ja DD' leikkaus­piste. Tässä kolline­aatiossa pisteen E kuvapiste E' on suorien A'I ja OE leikkaus­piste, missä I on suorien L ja AE leikkaus­piste.

Edellä homo­grafiat on määritelty lineaari­algebran avulla. Synteetti­sessä geometriassa ne on vanhastaan määritelty tiettyjen keskeis­kollineaatioiksi nimitettyjen homo­grafioiden yhdistetyiksi kuvauksiksi. Projektiivisen geometrian perus­lauseen yksi osa on se, että nämä määritelmät ovat yhtä­pitävät.

Projektiivisessa avaruudessa P, jonka ulottuvuus on n = 2, P:n kollineaatio on sellainen bijektio P:stä itselleen, jossa suorat kuvautuvat suoriksi. Keskeis­kollineaatio, jota ainakin aikaisemmin on sanottu myös perspek­tivi­teetiksi, on sellainen bijektio a P:stä itselleen, että on olemassa hypertaso H, jonka kaikki pisteet kuvautuvat itselleen (tätä hypertasoa sanotaan a:n akseliksi) ja piste O (jota sanotaan a:n keskukseksi), jonka kautta kulkevat suorat kuvautuvat kaikki itselleen (mikä ei kuitenkaan edellytä, että näiden suorien jokainen pistekin kuvautuisi itselleen.) Keskeisollineaatioita on kahta tyyppiä. Elaatiot ovat keskeis­kollinaatioita, joiden keskus sijaitsee akselilla, ja homologiat sellaisia, joiden keskus ei ole akselilla. Keskeis­kollinaation määräävät yksi­käsitteisesti keskus, akseli, yksi piste ja sen kuvapiste.

Keskeiskollineaatio on homogragia, joka määrittelee (n+1) × (n+1) -matriisi (homografiamatriisi), jolla on n-ulotteinen ominaisavaruus. Se on homologia, jos matriisilla on toinenkin ominaisarvo, jolloin se on dia­gonali­soituva. Se on elaatio, jos kaikki ominais­arvot ovat yhtä suuret eikä matriisi ole dia­gonali­soituva.

Keskeis­kollineaatioihin liittyvä geometrinen mieli­kuva on helpoin hahmottaa projek­tiivisen tason tapauksessa. Jos on annettu keskeis­kollineaatio a, tarkastellaan suoraa $\ell$, joka ei kulje keskuksen O kautta, ja suoraa $\ell '=\alpha (\ell )$, jolle a sen kuvaa. Jos asetetaan $R=\ell \cap \ell '$, a on jokin R:n kautta kulkeva suora M. Jokaisen suoralla $\ell$ oleva piste kuvautuu OA:n ja $\ell '$:n leikkaus­pisteeseen. Jos piste B ei ole suoralla $\ell$, sen kuvapiste saadaan seuraavasti: jos $S=AB\cap M,$, niin $B'=SA'\cap OB.$

Vaikka kahden keskeis­kollineaation yhdistetty kuvaus on edelleen homo­grafia, se ei yleensä ole keskeis­kollinaatio. Itse asiassa jokainen homografia saadaan yhdistettynä kuvauksesta äärellisestä määrästä keskeis­kollinaatioita. Synteettisessä geometriassa tätä ominaisuutta, joka on osa projektiivisen geometrian perus­lauseesta, pidetään homo­grafian määritelmänä.

Projektiivisen geometrian peruslause

Homografioiden lisäksi on muitakin kolline­aatioita. Erityisesti minkä tahansa kunnan F jokainen automorfismi s määrittelee kolline­aation jokaiselle F:n yli muodostetulle projek­tiiviselle avaruudelle; se muodostetaan soveltamalla kuvausta s kaikille tietyn pisteen homogeeni­sille koordi­naateille. Näitä kolline­aatioita sanotaan auto­morfi­siksi kolline­aatioiksi.

Projektiivisen geometrian peruslause käsittää seuraavat kolme väitettä:

1. Jos projektiiviselle avaruudelle P on valittu kaksi projek­tiivista kantaa, on yksi ja vain yksi P:n homo­grafia, joka kuvaa ensimmäisen kannan toiselle kannalle.
2. Jos projektiivinen avaruus P on vähintään kaksi­ulotteinen, jokainen P:n kollineaatio on auto­morfisen kolline­aation ja homografian yhdistetty kuvaus. Erityisesti reaali­lukujen kunnan yli muodostetuissa vähintään kaksi­ulotteisissa projek­tiivisissa avaruuksissa jokainen kollineaatio on homografia.
3. Jokainen homografia voidaan esittää yhdistettynä kuvauksesta äärellisestä määrästä perspek­tivi­teettejä. Erityisesti jos projektiivinen avaruus on vähintään kaksi­ulotteinen, jokainen homo­grafia voidaan esittää yhdistettynä kuvauksena äärellisestä määrästä keskeis­kollineaatioita.

Jos projektiiviset avaruudet määritellään aksioomien avulla, kuten synteettisessä geo­metriassa tehdään, lauseen kolmas osa on pelkkä määritelmä. Jos projek­tiiviset avaruudet sen sijaan määritellään lineaarialgebrallisesti, lauseen ensimmäinen osa seuraa suoraan määritelmästä.

Homografiaryhmät

Koska jokaisella homografialla on käänteiskuvaus ja homo­grafioiden yhdistetty kuvaus on myös homo­grafia, annetun projektiivisen avaruuden homografiat muodostavat ryhmän. Esimerkiksi Möbiuksen ryhmä on kompleksisen projek­tiivisen suoran homografia­­ryhmä. Homografia­ryhmiä sanotaan myös projektiivisiksi lineaarisiksi ryhmiksi.

Koska kaikki saman kunnan yli muodostetut yhtä moni­ulotteiset homografiat ovat isomorfisia, on samoin niiden homografia­ryhmien laita. Niitä voidaan sen vuoksi käsitellä yhtenä ryhmänä, joka vaikuttaa eri avaruuksissa, ja niiden merkinnässä onkin mukana vain ulottuvuus, ei mikään tietty projektiivinen avaruus.

Kunnan F yli muodostetun n-ulotteisen projektiivisen avaruuden homografiaryhmälle käytetään merkintää PGL(n + 1, F). Edellä esitetystä homografian määritelmästä seuraa, että PGL(n + 1, F) voidaan käsittää myös tekijäryhmäksi GL(n + 1, F) / F^*I, missä GL(n + 1, F) on kääntyvien matriisien yleinen lineaarinen ryhmä ja F^*I on F:n muiden kuin nolla-alkion ja (n + 1) × (n + 1) -yksikkömatriisin tulojen muodostama ryhmä.

Kun F on Galois'n kunta GF(q), homografia­ryhmälle käytetään merkintää Malline:Nobreak. Esimerkiksi PGL(2,7) vaikuttaa kahdeksaan pisteeseen äärellisen kunnan GF(7) yli muodostetun projektiivisella suoralla, kun taas PGL(2,4), joka on isomorfisen alternoivan ryhmän A₅ kanssa, on viisipisteisen projektiivisen suoran homografiaryhmä.

Kaksoissuhde

Homografiateorian kannalta on oleellista, että homografiassa neljän samalla suoralla olevan pisteen kaksoissuhde säilyy.

Jos kunnan F yli muodostetulta suoralta valitaan kolme pistettä, a, b, ja c, on olemassa yksi ja vain yksi sellainen homografia h tältä suoralta joukkoon F ∪ {∞}, että h(a) = ∞, h(b) = 0 ja h(c) = 1. Jos samalta suoralta valitaan neljäs piste, pisteiden a, b, c ja d kaksoissuhde, jota merkitään [a,b; c,d], määritellään pisteen d kuvapisteeksi h(d) kuvauksessa h. Toisin sanoen jos d:llä on homogeeniset koordinaatit [k : 1] pisteiden a, b ja c muodostamassa projektiivisen avaruuden kannassa, niin [a, b; c,d] = k.

Kirjallisuutta

• Patrick du Val: Homographies, quaternions and rotations. Oxford: Oxford Mathematical Monographs, 1964. Teoksen verkkoversio.
• Ewald Gunter: Geometry: An Introduction, s. 263. Wadsworth Publishing, 1971. ISBN 0-534-00034-7