Algebrallinen käyrä
Algebrallinen käyrä on varisto, jonka dimensio on yksi. Algebrallisten käyrien teoria kehitettiin pitkälti 1800-luvulla.
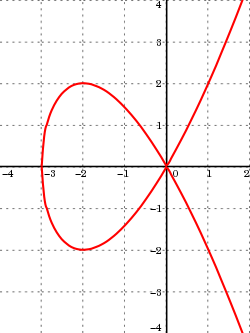
Algebrallinen käyrä kunnassa F voidaan käsittää niiden pisteiden uraksi tuloavaruudessa F'n, jotka saadaan vähintään n − 1 toisistaan riippumattoman polynomifunktion avulla, joiden kertoimet gi(x1, …, xn) kuuluvat kuntaan F, kun käyrän muodostavat ne pisteet, joissa gi = 0.
Algebralliset tasokäyrät
[muokkaa | muokkaa wikitekstiä]Tärkeän luokan algebrallisia käyriä muodostavat algebralliset tasokäyrät eli tasossa määritellyt algebralliset käyrät. Ne ovat jonkin kahden muuttujan polynomiyhtälön f(x, y) = 0 kuvaajia. Ne voidaan jaotella sen mukaan, kuinka monennen asteen polynomi on kyseessä.
Algebrallinen tasokäyrä voi leikata tasossa olevan suoran enintään niin monta kertaa kuin sen asteluku osoittaa.[1] Ensimmäisen asteen tasokäyrät ovat suoria. Niiden yhtälö on muotoa ax + by + c = 0, ja suora voi leikata toisen suoran vain yhdessä pisteessä.
Toisen asteen tasokäyrän yhtälön yleinen muoto on ax2 + bx + cy2 + dy + exy + f = 0, jossa osa kertoimista tosin voi olla nollia. Tällaiset käyrät ovat yleensä kartioleikkauksia: ympyröitä, ellipsejä, paraabeleja tai hyperbelejä, ja ne voivat leikata suoran enintään kahdessa pisteessä. Esimerkiksi yhtälön x2 + y2 = r2 kuvaaja on ympyrä, yhtälön y = ax2 kuvaaja paraabeli ja yhtälön xy = a kuvaaja hyperbeli. Erikoistapauksissa kuvaajana voi olla myös kaksi toisensa leikkaavaa suoraa (esimerkiksi yhtälöllä xy = 0, jonka kuvaajan muodostavat x- ja y-akselit), yksi piste (esimerkiksi yhtälöllä x2 + y2 = 0 tai tyhjä joukko (esimerkiksi yhtälöllä x2 + y2 = -r2
Yksinkertaisin kolmannen asteen käyrä on kuutioparaabeli y = x3. Tällainen käyrä voi leikata suoran enintään kolmessa pisteessä. Korkeamman asteen käyriä ovat Cassinin käyrä ja sen erikoistapaus lemniskaatta.
Muiden kuin tason suhteen esimerkiksi toroidaalisilla pinnoilla leikkaussäännöt eivät ole sellaisenaan voimassa, vertaa epäeuklidinen geometria.
Kompleksinen algebralinen käyrä on ekvivalentti kompleksianalyysin Riemannin pinnan kanssa.[2]
Katso myös
[muokkaa | muokkaa wikitekstiä]Lähteet
[muokkaa | muokkaa wikitekstiä]- ↑ David Bergamini: Lukujen maailma, s. 83. Suomentanut Pentti Jotuni. Sanoma Oy, Life-tietokirjat, 1972.
- ↑ Hyry, Eero: Virkaanastujaisluento uta.fi. Viitattu 13.09.2012.
