Venn-diagrammi

Venn vietti suuren osan elämästään Cambridgen yliopiston Gonville and Caius Collegessa, jonka ruokasalin ikkunaan on myöhemmin hänen muistokseen koristeltu Venn-diagrammi.

Venn-diagrammi, joka osoittaa, mitkä isot kirjaimet ovat samannäköisiä latinalaisissa, kreikkalaisissa ja kyrillisissä kirjaimistoissa. Alin ympyrä sisältää kyrilliset, ylemmistä ympyröistä vasemmanpuoleinen kreikkalaiset ja oikeanpuoleinen latinalaiset kirjaimet.

Venn-diagrammi on matematiikassa joukko-opissa käytettävä diagrammi. Sen kehitti filosofi ja matemaatikko John Venn vuonna 1881. Venn-diagrammi kuvaa matemaattiset tai loogiset suhteet joukkojen välillä, ja sillä voidaan esittää joukkojen väliset operaatiot. Normaalisti joukkoja kuvataan ympyröillä, jotka usein leikkaavat toisiaan. Jos joukkoja on enemmän kuin kolme, käytetään yleensä muitakin kuvioita kuin ympyröitä.

Venn-diagrammeja käytetään havainnollistamaan eri joukkojen tai käsitteiden välisiä suhteita, paitsi joukko-opin alkeiden opetuksessa, myös toden­näköisyys­laskennassa, logiikassa, tilasto­tieteessä, kieli­tieteessä ja tietojen­käsittely­opissa.

Esimerkki

Joukot A ja B.

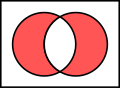
Kuvan esimerkissä näkyy joukot A ja B värillisinä ympyröinä. Oranssi ympyrä, joukko A, voi käsittää esimerkiksi kaikki kaksijalkaiset elävät olennot, sininen ympyrä, joukko B taas kaikki lentävät eläimet. Jokaista elävää olento voidaan ajatella vastaavan piste jossakin kohdassa diagrammeja. Kaksi­jalkaiset lento­kykyiset eläimet, kuten useimmat linnut kuuluvat molempiin joukkoihin, joten niitä vastaavat pisteet sijaitsevat molempien ympyröiden yhteisellä alueella. Sinne sijoittuvat siis kaikki eläimet, joilla on kaksi jalkaa ja jotka voivat lentää, ja vain ne.

Ihmiset ja pingviinit ovat myös kaksijalkaisia ja kuuluvat näin ollen oranssiin ympyrään, mutta koska ne eivät voi lentää, ne sijoittuvat oranssin ympyrän vasemman­puoleiseen osaan, joka jää sinisen ympyrän ulkopuolelle. Sääsket lentävät, mutta niillä on kuusi jalkaa, joten niitä vastaavat pisteet sijoittuvat siihen osaan sinistä ympyrää, joka jää oranssin ympyrän ulko­puolelle. Eläimet, jotka eivät ole kaksi­jalkaisia eivätkä lennä, esimerkiksi valaat ja hämähäkit, sijoittuvat molempien ympyröiden ulkopuolelle.

Aluetta, jonka muodostavat joukot A ja B yhdessä, sanotaan näiden joukkojen unioniksi ja merkitään A ∪ B. Tässä tapauksessa joukkojen unioniin kuuluvat kaikki elävät olennot, jotka ovat kaksijalkaisia tai voivat lentää, mukaan luettuna nekin, jotka täyttävät molemmat ehdot.

Sitä aluetta, jossa joukot A ja B ovat päällekkäisiä, sanotaan näiden leikkaukseksi ja merkitään A ∩ B. Tässä tapauksessa leikkaus ei ole tyhjä joukko, koska on pisteitä, jotka kuuluvat molempiin joukkoihin.

Joskus diagrammin ympärille piirretään nelikulmio, joka kuvaa universaalia perusjoukkoa. Tähän joukkoon kuuluu joukkojen A ja B lisäksi kaikki muut objektit tai asiat. Niiden laajuus riippuu otosavaruuden määritelmästä kyseisessä diagrammissa.

Historia

Venn-diagrammit otti käyttöön John Venn (1834–1923) aikakauskirjassa Philosophical Magazine and Journal of Science vuonna 1880 julkaisemassaan tutkielmassa On the Diagrammatic and Mechanical Representation of Propositions and Reasonings.

Venn itse nimitti näitä kaavioita Eulerin ympyröiksi (engl. Euler’s circles) koska Leonhard Euler oli jo yli sata vuotta aikaisemmin havainnollistanut loogisia syllogismeja oleellisesti samankaltaisilla kaavioilla teoksessaan Kirjeitä saksalaiselle prinsessalle fysiikasta ja filosofiasta. Nimitystä Venn-diagrammi käytti ensimmäisenä Clarence Irving Lewis vuonna 1918 teoksessaan "A Survey of Symbolic Logic".

Myöhemmin Ruskey ja M. Weston ovat huomauttaneet, että näiden muodollisessa logiikassa käytettävien diagrammien alkuperä ei ole helposti jäljitettävissä, mutta on varmaa, että niitä on käytetty kauan ennen Venniä. Heidän mukaansa nimitys Venn-diagrammi on kuitenkin oikeutettu, koska Venn teki niistä laajan yleiskatsauksen, formalisoi niiden käytön ja käytti eräitä niiden yleistyksiä ensimmäisenä. M. E. Baron on todennut, että kauan ennen Euleria, jo 1200-luvulla, samantyyppisiä diagrammeja oli käyttänyt Ramon Llull sekä myöhemmin Gottfried Wilhelm Leibniz (1646–1716), joskaan ei julkaisuissa teoksissaan.

Venn-diagrammeja kehitettiin edelleen 1900-luvulla. Vuonna 1963 D. W. Henderson osoitti, että n joukkoa kuvaava pyörähdyssymmetrinen Venn-diagrammi voi olla olemassa vain, jos n on alkuluku. Hän osoitti myös, että sellaiset symmetriset Venn-diagrammit todella voidaan muodostaa 5 ja 7 joukolle. Vuonna 2001 Peter Hamburger löysi symmetrisen Venn-diagrammin 11 joukolle, ja vuonna 2003 Griggs, Killian ja Savage todistivat, että se on mahdollista aina, kun joukkojen lukumäärä n on alkuluku. Täten pyörähdyssymmetrinen Venn-diagrammi on olemassa, jos ja vain jos n on alkuluku.

Kouluopetuksessa Venn-diagrammit ja Eulerin diagrammit tulivat käyttöön uuden matematiikan yhteydessä 1960-luvulla, kun kouluissa alettiin opettaa joukko-oppia. Myöhemmin niitä on alettu käyttää muidenkin aineiden, myös lukemisen opettamisessa.

Yleiskatsaus

• 
  Kahden joukon leikkaus
  $~A\cap B$
• 
  Kahden joukon unioni
  $~A\cup B$
• 
  Kahden joukon symmetrinen erotus$A~\Delta ~B$
• 
  Joukkojen A (vasemmalla) ja B (oikealla) joukkoerotus
  $A^{c}\cap B~=~B\setminus A$
• 
  Joukon A komplementti perusjoukossa U
  $A^{c}~=~U\setminus A$

Venn-diagrammi muodostetaan piirtämällä tasolle yksinkertaisia suljettuja käyriä. Lewisin mukaan näiden diagrammien periaatteena on, että joukkoja kuvataan alueilla siten, että jokaista mahdollisuutta kohti, jolla jokin alkio voi kuulua joihinkin näistä joukoista mutta ei välttämättä kaikkiin, vastaa jokin alue kaavioissa. Osa alueista voi olla tyhjiäkin, mikäli ei ole sellaista alkiota, joka kuuluisi vain tiettyihin joukkoihin mutta ei muihin.

Tavallisesti Venn-diagrammit muodostavat toisiaan leikkaavista ympyröistä. Ympyrän sisäpuolinen alue esittää symbolisesti sitä vastaavan joukon alkioita, ulkopuoli taas alkioita, jotka eivät kuulu kyseiseen joukkoon. Kahden joukon Venn-diagrammissa joukko A voisi esimerkiksi kuvata kaikkia puisia esineitä, toinen joukko B kaikkia pöytiä. Täten joukkojen leikkaus A ∩ B kuvaa kaikkia puisia pöytiä. Siinä osassa ympyrää A, joka jää ympyrän B ulkopuolelle, ovat esimerkiksi puiset tuolit sekä kaikki muutkin puusta tehdyt esineet, jotka eivät ole pöytiä. Vastaavasti siinä osassa ympyrää B, joka jää ympyrän A ulkopuolelle, ovat muista materiaaleista kuin puusta valmistetut pöydät. Jos joukkoja on enemmän kuin kolme, osaa niistä esittävät yleensä muut kuin ympyränmuotoiset alueet. Venn-diagrammit eivät yleensä sisällä tietoa joukkojen absoluuttisesta tai suhteellisesta suuruudesta eli kardinaliteetista, toisin sanoen ne ovat skemaattisia diagrammeja.

Venn-diagrammit muistuttavat huomattavasti Eulerin diagrammeja. Venn-diagrammi, jossa on n joukkoa, muodostetaan kuitenkin aina niin, että se käsittää kaikki 2ⁿ hypoteettista aluetta, jotka vastaavat kutakin sellaista tapaa, jolla alkio voi kuulua tai olla kuulumatta osaan näistä kuulumatta niihin kaikkiin. Eulerin diagrammeissa taas ympyrät piirretään siten, että jos joukkojen leikkauksista on tyhjä, vastaavat ympyrät ovat kokonaan toistensa ulkopuolella. Venn-diagrammissa varjostettu alue voi kuvata tyhjää joukkoa, kun taas Eulerin diagrammissa vastaavaa aluetta ei olekaan. Vastaavasti jos jokin joukoista on toisen osajoukko, sitä kuvaava ympyrä piirretään Eulerin, mutta ei Venn-diagrammeissa kokonaan tätä laajempaa joukkoa kuvaavan ympyrän sisäpuolelle. Jos esimerkiksi yhden joukoista muodostavat kaikki maitotuotteet, toisen kaikki juustot, näitä joukkoja kuvaavassa Venn-diagrammissa on alueensa sellaisillekin juustoille, jotka eivät olisi maitotuotteita. Kun juustoilla kuitenkin tarkoitetaan vain tietyn tyyppisiä maitotuotteita, Eulerin diagrammissa juustoja vastaava ympyrä piirretään kokonaan maitotuotteita vastaavan ympyrän sisälle siten, että tällaisia olemattomia tuotteita (juustoja, jotka eivät ole maitotuotteita) vastaavaa aluetta ei lainkaan muodostu. Kun kuvattavien joukkojen lukumäärä kasvaa, Eulerin diagrammit ovat tämän vuoksi usein yksinkertaisempia kuin vastaavat Venn-diagrammit, varsinkin jos ei-tyhjien leikkausten lukumäärä on pieni.

Ero Eulerin ja Venn-diagrammien välillä käy ilmi seuraavasta esimerkistä. Tarkastellaan kolmea joukkoa:

• $A=\{1,\,2,\,5\}$
• $B=\{1,\,6\}$
• $C=\{4,\,7\}$

Näiden joukkojen Venn- ja Euler-diagrammit ovat:

• 
  Euler-diagrammi
• 
  Venn-diagrammi

Laajennukset useampaan joukkoon

Venn-diagrammeissa kuvataan yleensä kaksi tai kolme joukkoa. Kun toisensa leikkaavien joukkojen määrä on suurempi, kuvasi Venn ne kolmen ympyrän lisäksi tietyllä määrällä lomittain kulkevia käyriä. Alla olevassa kaaviossa neljä toisensa leikkaavaa ympyrää muodostavat laajimman Venn-diagrammin, jolla on simpleksin symmetria ja joka voidaan esittää visuaalisesti. Kaavion 16 leikkausta vastaavat tesseraktin särmiä.

Jos joukkoja on vielä enemmän, diagrammin symmetrian rikkoutumista ei voida välttää. Venn itse katsoi löytäneensä "itsessään elegantteja symmetrisiä kuvioita", jotka esittävät suurempaa määrää joukkoja, ja hän kehitti alla kuvatu neljän joukon diagrammin, jossa käytetään ellipsejä. Hän kehitti myös tavan muodostaa Venn-diagrammi kuinka monelle joukolle tahansa. Tällöin aloitetaan kolmen ympyrän muodostamasta kaaviosta, johon jokaista uutta joukkoa kohti lisätään uusi käyrä, joka leikkaa kaikki aikaisemmat.

• 
  Vennin malli, kun joukkojen lukumäärä
  n = 3
• 
  n = 4
• 
  n = 5
• 
  n = 6
• 
  Ellipsejä käsittävä Venn-diagrammi 4 joukolle
• 
  Tämä Eulerin diagrammi ei ole Venn-diagrammi, koska siinä on (ulkopuolta lukuun ottamatta) vain 13 aluetta; ei ole aluetta, jossa vain sininen ja keltainen tai vain punainen ja vihreä ympyrä kohtaisivat.
• 
  Branko Grünbaumin muodostama viiden joukon Venn-diagrammi, joka muodostuu pyörähdyssymmetrisesti asetetuista yhtenevistä ellipseistä. Alueiden merkintäjä voidaan yksinkertaistaa, kun esimerkiksi A tarkoittaa aluetta A ∩ B^c ∩ C^c ∩ D^c ∩ E^c, vastaavasti BCE aluetta A^c ∩ B ∩ C ∩ D^c ∩ E
• 
  Pelkillä kolmiolla muodostettu Venn-diagrammi 6 joukolle.

Edwardsin Venn-diagrammit

• 
  Kolme joukkoa.
• 
  Neljä joukkoa.
• 
  Viisi joukkoa.
• 
  Kuusi joukkoa.

A. W. F. Edwards muodosti sarjan Venn-diagrammeja suuremmalle määrälle joukkoja jakamalla pallon pinnan segmentteihin. Esimerkiksi kolme aluetta voidaan helposti kuvata valitsemalla pallopinnalta kolme pallonpuoliskoa, joiden reunat leikkaavat toisensa kohtisuorasti (x = 0, y = 0 and z = 0). Neljäs joukko voidaan lisätä kaavioon käyttämällä käyrää, joka muistuttaa tennispallon saumaa leikaten päivän­tasaajan useita kertoja edestakaisin. Tuloksena saatavat joukot voidaan projisoida takaisin tasolle, jolloin saadaan yllä kuvatun kaltaiset, hammas­pyöriä muistuttavat kaaviot. Niissä on silloin sitä enemmän hampaita, mitä enemmän kuvattavia joukkoja on. Tällaiset diagrammit kehitettiin, kun Vennin muistoksi suunniteltiin lasi­maalauksella koristettua ikkunaa.

Muita diagrammeja

Edwardin Venn-diagrammit ovat topologisesti ekvivalentteja Branko Grünbaumin suunnittelemien diagrammien kanssa, jotka muodostuvat toisensa leikkaavista monikulmioista, joissa on kasvava määrä sivuja. Ne ovat samalla hyperkuutioiden kaksiulotteisia kuvauksia.

Henry John Stephen Smith kehitti n joukolle samantapaiset diagrammit käyttämällä sinikäyriä, joiden yhtälöt muodostavat sarjan

$y_{i}={\frac {\sin(2^{i}x)}{2i}}{\text{ where }}0\leq i\leq n-2{\text{ and }}i\in \mathbb {N} .$

Charles Lutwidge Dodgson muodosti myös oman diagramminsa viidelle joukolle.

Venn-diagrammit ja totuustaulut

Venn-diagrammi totuustauluna

Venn-diagrammit vastaavat totuustauluja lauseille $x\in A$, $x\in B$ jne. siinä mielessä, että jokaista Venn-diagrammin aluetta vastaa yksi totuustaulun rivi. Toisen tavan havainnollistaa joukkoja muodostavat Randolphin diagrammit.

Kirjallisuutta

• On the Diagrammatic and Mechanical Representation of Propositions and Reasonings. Dublin Philosophical Magazine and Journal of Science, 1880, 59. vsk, nro 9, s. 1–18. doi:10.1080/14786448008626877
• Lipschutz, Seymour: Set Theory and Related Topics. McGraw-Hill, 1964. ISBN 0-07-037986-6

Aiheesta muualla

• Venn diagram Encyclopedia of Mathematics, Springer. Viitattu 14.4.2015.
• Venn Diagram MathWorld. Viitattu 14.4.2015.
• Generalized Venn Diagrams 1987 (Arkistoitu – Internet Archive) by E. S. Mahmoodian, with M. Rezaie and F. Vatan.
• A Survey of Venn Diagrams by F. Ruskey and M. Weston, is an extensive site with much recent research and many beautiful figures.
• Lewis Carroll's Logic Game – Venn vs. Euler Cut-the-knot.org-sivustolla.
• A Survey of Venn Diagrams
• Generating Venn Diagrams to explore Google Suggest results
• seven sets interactive Venn diagram displaying color combinations
• six sets Venn diagrams made from triangles
• Postscript for 9-set Venn (Arkistoitu – Internet Archive) and more
• Venn diagram in Excel