Puolisuunnikas

Puolisuunnikas on geometriassa yksinkertainen nelikulmio, jonka kaksi vastakkaista sivua ovat keskenään yhdensuuntaiset. Toisinaan puolisuunnikkaalta vaaditaan, että täsmälleen yksi sivupari on yhdensuuntainen erotukseksi suunnikkaasta, jossa yhdensuuntaisia sivupareja on kaksi. Ellei nelikulmiolla ole yhdensuuntaisia sivupareja, on kuvio epäkäs.[1][2][3][4]
Ominaisuuksia
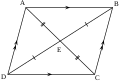
[muokkaa | muokkaa wikitekstiä]Seuraavassa viitataan oheiseen kuvaan ja sen merkittyihin osiin.
Sivut, lävistäjät, bimediaanit ja korkeusjanat
[muokkaa | muokkaa wikitekstiä]Puolisuunnikkaan sivut ovat yleensä eripituiset, mutta vähintään kaksi niistä on oltava yhdensuuntaisia. Kuviossa ne ovat sivut AB = a ja CD = c. Yhdensuuntaisia sivuja kutsutaan kannoiksi ja sivuja AD = d ja BC = b kutsutaan kyljiksi.[5][6]
Lävistäjät piirretään kulmasta vastakkaiseen kulmaan, joten niitä on kaksi: BD = q ja AC = r. Ne leikkaavat toisensa pisteessä E, joka jakaa kummankin lävistäjän samassa suhteessa osiin: AE : EC = BE : ED = a : c.[4]
Bimediaanit piirretään sivun keskipisteestä vastakkaisen sivun keskipisteeseen. Niitäkin on kaksi, joista m piirretään kantojen välille ja n kylkien välille. Kylkien välistä bimediaania kutsutaan englanninkielisessä kirjallisuudessa myös nimellä "median" ja se on yhdensuuntainen kantojen kanssa (a || m || c). Bimediaanit leikkaavat toisensa pisteessä F. Lävistäjien keskipisteet R ja Q sijaitsevat aina puolisuunnikkaan kylkiä yhdistävällä bimediaanilla n ja leikkauspiste E sijaitsee aina kannat yhdistävällä bimediaanilla m. Leikkauspisteet E ja F sijaitsevat yleensä eri kohdissa.[2][4]
Bimediaanien leikkauspisteen F fysikaalinen tulkinta liittyy painopisteeseen. Jos nelikulmien kärkiin sijoitetaan samansuuruiset painot, on F näiden painojen geometrinen painopiste. Tämä ominaisuus on yhteinen kaikille nelikulmioille.[7]
Puolisuunnikkaan korkeudella tarkoitetaan kantojen AB ja CD välistä etäisyyttä. Korkeusjana on mikä tahansa kantojen tai niiden jatkeiden välinen normaalin suuntainen jana. Se merkitään h = hac.
Kulmat
[muokkaa | muokkaa wikitekstiä]Puolisuunnikkaan sisäkulmien summa on α + β + γ + δ = 360°. Sisäkulmat ovat yleensä eri suuruiset. Ulkokulmat ovat sisäkulmien suplementtikulmat eli esimerkiksi kärjessä B on ι = 180° − β.[5]
Lävistäjät erottavat sisäkulmista kannan ja lävistäjän välisen kulman (neljä kappaletta), jotka ovat ristikkäin saman suuruiset: ja Usein on Näiden yhtäsuuruuksien vuoksi kolmiot ΔAEB ja ΔCED ovat yhdenmuotoiset.
Lävistäjät leikkaavat toisensa pisteessä E kulmassa ε tai θ, jotka ovat toistensa vieruskulmia eli ε + θ = 180°. Molemmilla kulmilla on ristikulmat, mikä on merkitty näkyviin kulmalle ε.
Bimediaanit leikkaavat toisensa pisteessä F kulmassa ζ. Silläkin on luonnollisella tavalla risti- ja vieruskulmat.
Pituusmittoja
[muokkaa | muokkaa wikitekstiä]Pinta-ala
[muokkaa | muokkaa wikitekstiä]Puolisuunnikkaan pinta-ala voidaan laskea esimerkiksi kylkiä yhdistävän bimediaanin avulla. Kylkien välinen bimediaani n on yhdensuuntaisten sivujen a ja c pituuksien keskiarvo. Pinta-alan laskeminen yksinkertaistuu ja palautuu n leveän ja h korkeaan suorakulmion laskemiseen: [8][9][6][2]
Pinta-ala voidaan laskea, vaikka tunnetaan vain sivujen pituudet (yhdensuuntaisia ovat a || c):[2]
Puolisuunnikas voidaan jakaa neljäksi kolmioksi lävistäjien AC = r ja BD = q avulla, jolloin nämä leikkaavat toisensa pisteessä E. Tällöin kylkien puoleiset kolmiot ovat pinta-alaltaan yhtä suuret (ΔAED = ΔBEC). Lisäksi kylkien puoleisten kolmioiden alojen tulo on yhtäsuuri kuin kantojen puoleisten kolmioiden alojen tulo (ΔAED × ΔBEC = ΔAEB × ΔCED). Kahden vierekkäisen kolmion pinta-alojen suhde on yhtä suuri kuin yhdensuuntaisten sivujen suhde: ΔAEB : ΔAED = ΔAEB : ΔBEC = ΔBEC : ΔCED = ΔAED : ΔCED = a : c.[2]
Erityisiä puolisuunnikkaita
[muokkaa | muokkaa wikitekstiä]Tasakylkinen puolisuunnikas
[muokkaa | muokkaa wikitekstiä]
Tasakylkisessä puolisuunnikkaassa kyljet ovat yhtä pitkät, jolloin myös kantakulmat ovat yhtä suuret. Samalla puolisuunnikas muuttuu symmetriseksi ja kannat yhdistävä bimediaani on tällöin symmetria-akselina. Se on myös syklinen monikulmio, jonka ympäröivän ympyrän keskipiste sijaitsee symmetria-akselilla.[10][5][11]
Suorakulmainen puolisuunnikas
[muokkaa | muokkaa wikitekstiä]
Suorakulmaisella puolisuunnikkaalla on kaksi suoraa kulmaa, joita yhdistää toinen korkeusjanaksi kutsuttava kylki. Kantojen toinen kulma on siten suora.[12]
Suunnikas ja neljäkäs
[muokkaa | muokkaa wikitekstiä]Suunnikas ja neljäkäs ovat puolisuunnikkaiden erikoistapauksia, koska niillä on kaksi yhdensuuntaista sivuparia (jos käytetään määritelmää: vähintään yksi yhdensuuntainen sivupari). Lisäksi ne ovat tasakylkisiä puolisuunnikkaita.[5][13][14]
-
Suunnikas
-
Neljäkäs
Suorakulmio ja neliö
[muokkaa | muokkaa wikitekstiä]Suorakulmio ja neliö ovat suunnikkaana myös puolisuunnikkaita. Ne ovat erityisesti tasakylkisiä ja suorakulmaisia puolisuunnikkaita.[15][16]
-
Suorakulmio
-
Neliö
Lähteet
[muokkaa | muokkaa wikitekstiä]- Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
- Alatupa, Sami et al.: Pitkä Sigma 3. (lukion pitkän matematiikan oppikirja) Helsinki: Otava, 2008. ISBN 978-951-26-5927-2
- Kontkanen, Pekka & al.: Pyramidi 3. (lukion pitkän matematiikan oppikirja) Helsinki: Tammi, 2005. ISBN 978-951-26-5059-0
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ Väisälä, Kalle: Geometria, 1959, s. 22
- ↑ a b c d e f g h i j k l Weisstein, Eric W.: Trapezoid (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Kivinen, s. Albert: Analyysin paradoksi (Arkistoitu – Internet Archive), Tieteessä tapahtuu
- ↑ a b c King, James: Trapezoids, Univercity of Washington, Seattle, USA
- ↑ a b c d Alatupa, Sami & al.:Pitkä Sigma 3, 2008, s. 21–22
- ↑ a b Kontkanen, Pekka & al.: Pyramidi 3, 2005, s. 44–55
- ↑ Weisstein, Eric W.: Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Väisälä, Kalle: Geometria, 1959, s. 45
- ↑ Alatupa, Sami & al.:Pitkä Sigma 3, 2008, s. 73
- ↑ Weisstein, Eric W.: Isosceles Trapezoid (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Jukka Kangasaho, Jukka Mäkinen, Juha Oikkonen, Johannes Paasonen, Maija Salmela: Geometria (Pitkä matematiikka). (Tehtävä 146, s. 65) WSOY, 2001. ISBN 951-0-24558-5
- ↑ Weisstein, Eric W.: Right Trapezoid (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Parallelogram (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Rhombus (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Square (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Rectangle (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä]- Geometry: Trapezoid (Arkistoitu – Internet Archive)
- Math Open Reference: Median of a trapezoid
- Cut the Knots: Centroids in Polygon: What is it about?