Kärki (geometria)




Kärki on geometriassa ja avaruusgeometriassa tietynlainen piste, jollainen on monikulmion sivun tai avaruuskappaleen särmän molemmissa päissä tai monikulmaisen tahkon jokaisessa kulmassa.
Määritelmiä
[muokkaa | muokkaa wikitekstiä]Kulman kärki
[muokkaa | muokkaa wikitekstiä]Kulma syntyy, kun kaksi puolisuoraa tai janaa leikkaavat yhteisessä pisteessä ja suorien väliin jää kiilamainen alue. Tätä kutsutaan kulmaksi, jonka kärki on mainittu leikkauspiste.
Monikulmion kärki
[muokkaa | muokkaa wikitekstiä]Monikulmio syntyy kaksiulotteisessa tasossa, kun kolme tai useampi jana yhdistetään päätepisteistään toisiinsa ketjuksi ja äärimmäisten janojen vapaat päätepisteet yhdistetään. Jokaisen janan päätepiste on tällöin monikulmion kärki.
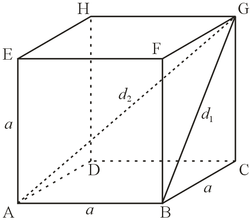
Monitahokkaan kärki
[muokkaa | muokkaa wikitekstiä]Monitahokas syntyy kolmiulotteisessa avaruudessa, kun neljä tai useampi erisuuntainen taso leikkaa toisensa. Jokainen taso toimii monitahokkaan tahkona. Tasojen leikkauskuvioina syntyy joukko suoria, joita kutsutaan särmiksi. Särmät leikkaavat toisensa pisteissä, joita kutsutaan monitahokkaan kärjiksi.
Katso myös
[muokkaa | muokkaa wikitekstiä]Lähteet
[muokkaa | muokkaa wikitekstiä]- Väisälä, Kalle: Geometria, s. 156–158. Helsinki: Wsoy, 1959. Teoksen verkkoversio (pdf) Viitattu 5.5.2016.
- Alatupa, Sami et al.: Pitkä Sigma 3. (lukion pitkän matematiikan oppikirja) Helsinki: Tammi, 2008. ISBN 978-951-26-5927-2
- Weisstein, Eric W.: Polygon Vertex (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Weisstein, Eric W.: Polyhedron Vertex (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Weisstein, Eric W.: Principal Vertex (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
