Kolmion keskinormaalien leikkauspiste

Keskinormaalit leikkaavat toisensa yhteisessä pisteessä.

Kolmion keskinormaalien leikkauspiste on geometriassa piste, joka syntyy jokaisen sivun keskinormaalin kohdatessa toisensa. Leikkauspiste on eräs kolmion merkillisestä pisteistä ja se on luetteloitu Kimberlingin pisteiden luetteloon tunnuksella $\scriptstyle X_{3}$. Pisteen nimeksi on valittu monissa kielissä melko samantapainen termi, joka kirjoitetaan englanniksi circumcenter. Se viittaa kolmion ympärille piirrettyyn ympyrään, jonka keskipiste yhtyy leikkauspisteeseen.

Sijainti kolmiossa

Keskinormaalit ovat kohtisuorassa kolmion sivuihin nähden. Kahden sivun välinen tylppä kulma voi kääntää kahden sivun keskinormaalit lähes yhdensuuntaisiksi, jolloin niiden leikkauspiste jää kauaksi. Leikkauspiste voi siksi sijaita tietysti kolmion sisällä, mutta myös kaukana kolmion ulkopuolella.

• 
  Teräväkulmaisessa kolmiossa leikkauspiste jää kolmion sisälle.
• 
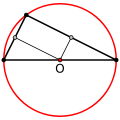
  Suorakulmaisessa kolmiossa leikkauspiste osuu hypotenuusalle.
• 
  Tylppäkulmaisella kolmiolla leikkauspiste on kolmion ulkopuolella.

Kolmion ympäri piirretty ympyrän leikkauspiste sijaitsee samassa kohtaa keskinormaalien (punaiset suorat) leikkauspisteen H kanssa. Säteet on merkitty sinisellä.

Sivun keskinormaali on suora, jonka pisteet sijaitsevat yhtä kaukana molemmista sivun päätepisteistä. Kun näin on laita kaikille kolmion keskinormaaleille, ovat keskinormaalien leikkauspisteen etäisyydet kaikkiin kolmion kärkiin yhtä pitkät. Jos kolmion kärkien kautta piirtää ympyrän, tulee sen säteeksi leikkauspisteen etäisyys kolmion kärkiin.

Kun kolmion sivujen pituudet merkitään $a,\,b\ ja\ c$ on säteen $R$ pituus

$R={\frac {abc}{\sqrt {(a+b+c)(b+c-a)(c+a-b)(a+b-c)}}}.$

Kun kolmiosta tunnetaan kärkiä $A,\,B\ ja\ C$ vastaavat kulmat $\alpha \,\,\beta \ ja\ \gamma$, saadaan Sinilauseesta

$R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}.$

Karteesit koordinaatit

Kolmion kolme kärkeä merkitään $A(x_{a},y_{a})$, $B(x_{b},y_{b})$, ja $C(x_{c},y_{c})$. Leikkauspisteen $O(x_{o},y_{o})$ koordinaatit ovat silloin

$x_{o}=((x_{a}^{2}+y_{a}^{2})(y_{b}-y_{c})+(x_{b}^{2}+y_{b}^{2})(y_{c}-y_{a})+(x_{c}^{2}+y_{c}^{2})(y_{a}-y_{b}))/D,$

$y_{o}=((x_{a}^{2}+y_{a}^{2})(x_{c}-x_{b})+(x_{b}^{2}+y_{b}^{2})(x_{a}-x_{c})+(x_{c}^{2}+y_{c}^{2})(x_{b}-x_{a}))/D,$

missä

$D=2(x_{a}(y_{b}-y_{c})+x_{b}(y_{c}-y_{a})+x_{c}(y_{a}-y_{b})).\,$

Trilineaariset koordinaatit

Pisteen trilineaariset koordinaatit ovat :$\cos \alpha \,:\,\cos \beta \,:\,\cos \gamma =a(b^{2}+c^{2}-a^{2})\,:\,b(c^{2}+a^{2}-b^{2})\,:\,c(b^{2}+a^{2}-c^{2})$.

Barysentriset koordinaatit

Pisteen barysentriset koordinaatit ovat

$\sin 2\alpha \,:\,\sin 2\beta \,:\,\sin 2\gamma =a^{2}(b^{2}+c^{2}-a^{2})\,:\,b^{2}(c^{2}+a^{2}-b^{2})\,:\,c^{2}(b^{2}+a^{2}-c^{2})$.

Muuta

Eulerin suora

Jos varhain huomattiin, että keskinormaalin leikkauspiste ($\scriptstyle X_{3}$) on kollineaarinen kolmion painopisteen ($\scriptstyle X_{2}$), ortokeskuksen ($\scriptstyle X_{4}$) ja yhdeksän pisteen ympyrän keskipisteen ($\scriptstyle X_{5}$) kanssa. Näiden kautta kulkevaa suoraa kutsutaan Eulerin suoraksi.

Etäisyyksiä

Painopiste G ja ortokeskus O sijaitsevat kolmion muodosta riippumatta Eulerin suoralla tasavälein niin, että HG = 2•GO.

Kolmiota ympäröivän ympyrän (säde R) keskipiste eli kolmion keskinormaalien leikkauspiste O ja painopiste G toteuttavat yhtälön $\scriptstyle GO^{2}=R^{2}-{\tfrac {1}{9}}(a^{2}+b^{2}+c^{2})$

Lähteet

• Koivulahti, Perttu: Trilineaariset koordinaatit (pdf) (tutkielma) 2012. Jyväskylä: Jyväskylän Yliopisto. Viitattu 20.4.2013.
• Harju, Tero: Geometrian lyhyt kurssi (pdf) (luentomoniste) users.utu.fi. 2012. Turun yliopisto. Viitattu 20.4.2013.
• Kurittu Lassi: Geometria (pdf) (luentomoniste) 2006. Jyväskylän: Jyväskylän Yliopisto. Viitattu 20.4.2013.