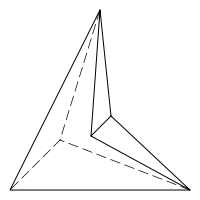
Heksaedri

Wikipediasta
Siirry navigaatioon Siirry hakuun
Osa artikkelisarjaa
Tasogeometria

Heksaedri eli 6-tahokas tai kuusitahokas on monitahokas, jonka pinnan muodostaa kuusi monikulmiota eli tahkoa.[1] Säännöllistä heksaedria kutsutaan kuutioksi.[2] Kuutio on yksi Platonin kappaleista. Muita erityisiä heksaedreja ovat muun muassa kaksi kultaista romboedria.

Luokittelu

[muokkaa | muokkaa wikitekstiä]

Erään luokittelutavan mukaan kuperia heksaedreja on seitsemänlaisia.[3] Luokittelu perustuu siihen, minkälaiset heksaedrin tahkot ovat. Luokittelun mukaan esimerkiksi kuutiot ja nelikulmiotahkoiset katkaistut kartiot kuuluvat samaan luokkaan. Alla on kuva jokaisen luokan esimerkkiheksaedrista. Esimerkiksi merkintä (5,3,3,3,3,3) tarkoittaa, että monitahokkaan yksi tahko on viisikulmio ja loput kuusi tahkoa ovat kolmioita.

  • Tahkot: 4,4,4,4,4,4
  • 8 kärkeä
  • 12 särmää
  • Tahkot: 5,3,3,3,3,3
  • 6 kärkeä
  • 10 särmää
  • Tahkot: 5,4,4,3,3,3
  • 7 kärkeä
  • 11 särmää
  • Tahkot: 5,5,4,4,3,3
  • 8 kärkeä
  • 12 särmää
  • Tahkot: 3,3,3,3,3,3
  • 5 kärkeä
  • 9 särmää
  • Tahkot: 4,4,4,4,3,3
  • 7 kärkeä
  • 11 särmää

Kappale on kiraalinen.

  • Tahkot: 4,4,3,3,3,3
  • 6 kärkeä
  • 10 särmää

Mikäli otetaan mukaan vielä koveratkin heksaedrit, luokkia tulee kolme lisää:

  • Tahkot: 4,4,3,3,3,3
  • 6 kärkeä
  • 10 särmää
  • Tahkot: 5,5,3,3,3,3
  • 7 kärkeä
  • 11 särmää
  • Tahkot: 6,6,3,3,3,3
  • 8 kärkeä
  • 12 särmää

Esimerkkejä joistakin nelikulmiotahkoisista heksaedreistä

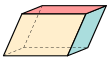
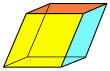
[muokkaa | muokkaa wikitekstiä]
Joitakin nelikulmiotahkoisia (4,4,4,4,4,4) heksaedreja: 6 tahkoa, 12 särmää, 8 kärkipistettä
Kuutio
(neliöt) 		Suorakulmainen särmiö
(kolme paria
suorakulmiota) 		Trigonominen trapetsoedri
(yhtenevät neljäkkäät) 		Trigonominen trapetsoedri
(yhtenevät nelikulmiot) 		Nelikulmiotahkoinen katkaistu kartio
(neliö ja neljä puolisuunnikasta) 		Suuntaissärmiö
(kolme paria
suunnikkaita) 		Suuntaissärmiö
(kolme paria
neljäkkäitä)

Katso myös

[muokkaa | muokkaa wikitekstiä]

Lähteet

[muokkaa | muokkaa wikitekstiä]

Viitteet

[muokkaa | muokkaa wikitekstiä]
  1. ↑ Matematiikan verkkosanakirja Matematiikkalehti Solmu.
  2. ↑ ”A - Isonzo”, Pieni Tietosanakirja, s. 1159. (Projekti Runebergin digitaalinen näköispainos teoksesta Pieni Tietosanakirja) Helsinki: Otava, 1925–1928. Teoksen verkkoversio (TIFF G4 -tiedosto).
  3. ↑ Hexahedron mathworld.wolfram.com. Viitattu 13.7.2020. (englanniksi)

Aiheesta muualla

[muokkaa | muokkaa wikitekstiä]
Tämä matematiikkaan liittyvä artikkeli on tynkä. Voit auttaa Wikipediaa laajentamalla artikkelia.
Noudettu kohteesta ”https://fi.wikipedia.org/w/index.php?title=Heksaedri&oldid=22209158”