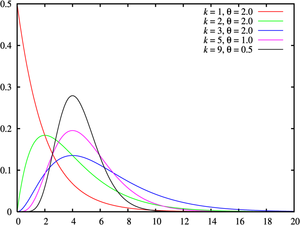
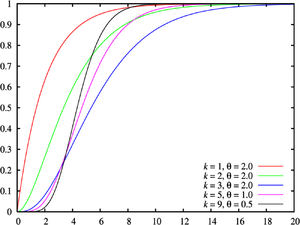
Gamma-jakauman tiheysfunktion kuvaajia eri parametriparein Gamma-jakauman kertymäfunktion kuvaajia eri parametriparein Gamma-jakauma on Poisson-prosessin insidenssien odotusaikojen jakauma .
Gamma-jakauma on jatkuva, ja sen arvojoukko on positiivisten reaalilukujen joukko. Jos satunnaismuuttuja
X
{\displaystyle X}
gamma-jakautunut , merkitään
X
∼
Gamma
(
ν
,
λ
)
.
{\displaystyle X\sim \operatorname {Gamma} (\nu ,\lambda ).}
Jakauman parametrit toteuttavat ehdon
ν
,
λ
>
0
{\displaystyle \nu ,\lambda >0}
n
∈
N
{\displaystyle n\in \mathbb {N} }
Gamma
(
n
,
λ
)
{\displaystyle \operatorname {Gamma} (n,\lambda )}
n
{\displaystyle n}
λ
{\displaystyle \lambda }
Tiheysfunktio on arvojoukossa
f
X
(
x
)
=
λ
ν
Γ
(
ν
)
x
ν
−
1
e
−
λ
x
,
{\displaystyle f_{X}(x)={\frac {\lambda ^{\nu }}{\Gamma (\nu )}}x^{\nu -1}e^{-\lambda x},}
missä
Γ
{\displaystyle \Gamma }
gammafunktio . Kertymäfunktiota ei voi yleisessä tapauksessa esittää suljetussa muodossa. Odotusarvo ja varianssi ovat
E
(
X
)
=
ν
λ
{\displaystyle \operatorname {E} (X)={\frac {\nu }{\lambda }}}
Var
(
X
)
=
ν
λ
2
.
{\displaystyle \operatorname {Var} (X)={\frac {\nu }{\lambda ^{2}}}.}
Yhteydet eksponenttijakaumaan ja χ2 -jakaumaan :
Gamma
(
1
,
λ
)
=
Exp
(
λ
)
.
{\displaystyle \operatorname {Gamma} (1,\lambda )=\operatorname {Exp} (\lambda ).}
ja jos
n
∈
N
+
{\displaystyle n\in \mathbb {N} _{+}}
Gamma
(
n
2
,
1
2
)
=
χ
n
2
.
{\displaystyle \operatorname {Gamma} \left({\frac {n}{2}},{\frac {1}{2}}\right)=\chi _{n}^{2}.}
Diskreettejä jakaumia Jatkuvia jakaumia Moniulotteisia jakaumia