Nelikulmio

Nelikulmio eli tetragoni on geometriassa monikulmio^[1], jossa on neljä kulmaa ja sivua. Nelikulmio voidaan ajatella syntyvän murtoviivasta, jonka neljä sivua voivat olla eri asennoissa ja jonka ensimmäisen ja viimeisen sivun päätepisteet on yhdistetty toisiinsa. Murtoviivaa kutsutaan piiriksi. Nelikulmiosta voi tulla yksinkertainen tai kompleksinen monikulmio. Yhdessä kolmioiden kanssa nelikulmiot ovat yleisimmät geometriset kuviot ja tunnetuimpia nelikulmiota ovat neliöt, suorakulmiot, neljäkkäät, suunnikkaat ja puolisuunnikkaat.^[2]^[3]

Nelikulmiolla on neljä sivua ja yhdestä kärjestä erkanee aina puolet sivuista. Jos sivut numeroidaan juoksevasti yhdestä kärjestä lukien, ovat parilliset sivut toisilleen vastakkaiset sivut, kuten ovat myös parittomat sivut. Kulmille ja kärjille löytyvät vastaavasti vastakkaiset kärjet ja kulmat. Nelikulmion lävistäjät piirretään yhdistämällä vastakkaiset kärjet toisiinsa, joten lävistäjiä on aina kaksi. Ne voivat kulkea nelikulmion sisä- tai ulkopuolella.^[2]^[4]

Nelikulmioiden luokittelu

Nelikulmioita voi luokitella eri ryhmiin eri asioiden perusteella. Seuraavassa kaaviossa ja sitä seuraavassa tekstiosuudessa on esitelty joitakin luokkia, jotka ovat yleisimmin esillä sekä joitakin harvinaisempia tapauksia.

Kompleksinen nelikulmio

Kompleksista nelikulmiota kutsutaan joskus ”perhoseksi” tai ”rusetiksi”. Nelikulmion piiri leikkaa itseään vastakkaisten sivujen välissä ja muodostaa kaksi kolmion muotoista sisäosaa. Leikkauspiste ei kuitenkaan ole monikulmion kärki, vaikka siinä näyttää olevan ristikkäiset sisäkulmat. Jos sen kulmissa olisi kärkipiste, olisi se kaksiosainen kuusikulmio. Itseään leikkaavan nelikulmion lävistäjät kulkevat nelikulmion ulkopuolella.^[3]^[4]^[5]

Itseään leikkaava nelikulmio voi olla tasakulmainen, jos kummankin sisäosan sisäkulmat ovat yhtä suuret. Silloin risteävät sivut leikkaavat toisensa pisteessä, jonka etäisyydet yhdensuuntaisista poikittaisista sivuista voivat olla eri pituiset. Se ei kuitenkaan voi olla tasasivuinen. Sen risteävät sivut tulisivat tällöin olla pitemmät, jotta sisäosalle jäisi tilaa, mutta se olisi tasasivuisuutta vastaan. Itseään leikkaavassa nelikulmiossa on eräs merkillinen piirre. Kun lähtee liikkeelle yhdestä kärjestä ja seuraa piiriä, sijaitsee nelikulmion sisäosa kummassakin kolmiossa eri puolella kuljettavaa murtoviivaa. Samoin sisäkulmat aukeavat eri kolmiossa eri puolelle murtoviivaa.^[5]

Yksinkertaiset nelikulmiot

Monikulmio on yksinkertainen, kun sillä on yksi yhtenäinen sisäosa. Yksinkertainen nelikulmio voi olla konveksi- tai konkaavi monikulmio.^[4] Jos sillä ei ole yhtään yhdensuuntaista sivuparia, on se epäkäs.^[6]

Konveksit eli kuperat nelikulmiot

Konveksissa eli kuperassa nelikulmiossa kaikki kulmat ovat alle 180°, eli ne ovat koveria. Sisäkulmien eksplementtikulmat ovat silloin kuperia, jolloin koko nelikulmio on kupera.^[1] Tällöin mistä tahansa nelikulmion piirin pisteestä näkee sisäosan kautta suoraan kaikki muut piirin pisteet. Erityisesti kärjistä piirretyt molemmat lävistäjät kulkevat koko matkan nelikulmion sisäosassa.^[3]

Konveksin nelikulmion (kulmien lukumäärä n = 4) sisäkulmien summa on

S=(n-2)\cdot 180^{\circ }=(4-2)\cdot 180^{\circ }=360^{\circ }.

^[1]^[7]^[2]^[8]

Ulkokulma tarkoittaa monikulmiossa kulmaa, joka jää sivun jatkeen ja viereisen sivun väliin. Sisäkulman ja ulkokulman summa on aina 180° eli ne ovat toistensa suplementtikulmia. Konveksin monikulmion ulkokulmien summa on aina 360° eikä se riipu kulmien lukumäärästä.

Jos yksi kulma on lähes 180° eli oikokulma, jää muille kulmille yli 180°. Siksi kuperalla nelikulmiolla on mahdollista olla kaksi lähes 180° kulmaa, ja ne voivat sijaita vierekkäin tai vastakkain. Tällöin kahdelle muulle kulmalle jää jäljelle hyvin pienet kulmat ja nelikulmio on hyvin ohut.

Konkaavit eli koverat nelikulmiot

Konkaavi eli kovera nelikulmio voi syntyä vain siten, että yksi kulmista on kupera kulma. Kuperan kulman eksplementtikulma on tällöin kovera, mikä on antanut monikulmioluokalle sen nimen. Toista kuperaa kulmaa ei voi olla, sillä jo yhden kuperan kulman α takia (α > 180°) muille kolmelle kulmalle jää yhteensä 360° − α < 180°. Tämä johtuu siitä, että sisäkulmien summa on myös konkaaville nelikulmiolle sama 360°. Suurin kulma on siten vastakkainen kulma ja se on aina pienempi kuin 180° eli oikokulma.^[3]

Konkaavi nelikulmio ei voi olla syklinen tai tangentiaalinen nelikulmio, koska yksi kulmista on kupera. Se ei voi olla suunnikas eikä tasasivuinenkaan. Konkaavin nelikulmion lävistäjistä toinen kulkee sen sisäpuolella ja toinen ulkopuolella eivätkä ne silloin leikkaa toisiaan janoina. Lävistäjien jatkeet sen sijaan leikkaavat toisensa. Nelikulmio onkin yksinkertaisin konkaavi monikulmio, sillä kolmio ei voi olla konkaavi.

Erityisiä nelikulmioita

Neliö

Neliö on säännöllinen nelikulmio, jossa kaikki neljä kulmaa ovat suorina yhtä suuret eli 90° (tasakulmainen) ja sivut yhtä pitkät (tasasivuinen). Neliön lävistäjät ovat yhtä pitkät ja ne leikkaavat toisensa kohtisuoraan. Lävistäjät jakavat sen neljään kolmioon, jotka ovat kaikki tasasivuisia. Neliö on symmetrinen kahdeksan akselin suhteen, ja sen keskipiste sijaitsee lävistäjien leikkauspisteessä. Neliön ympäri ja sisään voi piirtää ympyrät, joten se on myös syklinen- ja tangentiaalinen nelikulmio (katso alempaa).^[2]^[9]^[10]

Suorakulmio

Suorakulmio eli suorakaide ^[9] on tasakulmainen nelikulmio, kuten neliökin, mutta sen sivut voivat olla eri pituiset. Tasakulmaisuudesta johtuu, että vastakkaiset sivut ovat saman pituiset ja yhdensuuntaiset, ja siksi suorakulmio kuuluu suunnikkaiden luokkaan. Suorakulmion lävistäjät ovat yhtä pitkät, ja ne leikkaavat samassa pisteessä kuin sen kaksi kohtisuoraa symmetria-akseliakin. Lävistäjät jakavat sen neljään kolmioon, jotka ovat pareittain yhtenevät. Suorakulmion ympäri voi piirtää ympyrä, joten myös se on syklinen. Neliö on suunnikkaan ja erityisesti neljäkkään erikoistapaus.^[2]^[1]

Neljäkäs

Neljäkäs eli vinoneliö ^[2] on suunnikas, jossa kaikki sivut ovat yhtä pitkät eli neljäkäs on tasasivuinen nelikulmio. Myös neljäkkään vastakkaiset kulmat ovat yhtä suuret ja vierekkäiset ovat toistensa suplementtiset parit. Jos neljäkkään kulmat ovat suorat eli 90°, se on neliö. Neljäkkään puolittavat toisensa ja leikkaavat toisensa kohtisuoraan sekä jakavat sen neljään kolmioon, jotka ovat kaikki keskenään yhtenevät.^[2]^[8]^[9]^[11]

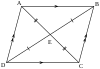
Suunnikas

Suunnikas on nelikulmio, jossa vastakkaiset sivut ovat pareittain yhdensuuntaiset ja yhtä pitkät. Suunnikkaassa on siten kahden pituisia sivuja ja kahden suuruisia kulmia. Vierekkäiset kulmat ovat toistensa suplementtikulmia ja vastakkaiset sisäkulmat aina yhtä suuret. Sen lävistäjät ovat eri pituisia, mutta jakavat sisäosan neljään kolmioon, jotka ovat pareittain yhtenevät. Lävistäjät myös jakavat toisensa puoliksi. Jos kulmat ovat suorat eli 90°, saadaan suorakulmio tai neliö.^[2]^[8]^[1]^[9]

Puolisuunnikas

Puolisuunnikas on nelikulmio, jossa vain yhdet vastakkaiset sivut ovat yhdensuuntaiset ja muut kaksi sivua erisuuntaiset. Erisuuntaisen sivun kummatkin sisäkulmat ovat toistensa suplementtikulmia. Lävistäjät ovat eri pituiset.^[1]^[9] Epäkäs on nelikulmio, jolla ei ole yhdensuuntaisia sivuja.^[6]

Tasakylkinen puolisuunnikas

Tasakylkinen puolisuunnikas on puolisuunnikas, jonka erisuuntaiset sivut ovat yhtä pitkät. Se jakaa puolisuunnikkaan ominaisuudet, mutta sen kantakulmat ovat yhtä suuret, kuten ovat myös sen ”huippukulmat”. Symmetriasta johtuu, että sen lävistäjät ovat yhtä pitkät.^[2]^[8]

Syklinen nelikulmio

Syklisen nelikulmion eli jännenelikulmion ^[12] ympäri voidaan piirtää ympyrä siten, että kaikki kärjet ovat ympyrän kehällä. Tämä ehto aiheuttaa nelikulmiolle joukon säännönmukaisuuksia, joita voidaan käyttää ympyröiden ja suorien kohtaamisissa. Esimerkiksi vastakkaiset kulmat ovat aina suplementtikulmia. Lävistäjät toteuttavat erityisiä ehtoja, mutta ovat eri pituiset. Syklinen nelikulmio on aina konveksinen.^[13]

Tangentiaalinen neljäkäs.

Tangentiaalinen nelikulmio

Tangentiaalisen nelikulmion sisäpuolelle voidaan piirtää ympyrä siten, että kaikki sivut sivuavat ympyrää tangentteina. Lävistäjät ovat eri pituiset ja kulmanpuolittajat näyttelevät siksi suurempaa roolia nelikulmion ominaisuuksissa. Koska nelikulmion sivut kiertävät ympyrää, on se aina konveksi nelikulmio.^[14] Pitot'n lauseen mukaan tangentiaalisen nelikulmien vastakkaisten sivujen pituuksien summa on vakio. Steiner todisti vuonna 1846, että jos nelikulmion vastakkaisten sivujen pituuksien summa on vakio, on nelikulmio tangentiaalinen.^[15]

Bisentrinen nelikulmio

Bisentrinen nelikulmio on samalla sekä syklinen- että tangentiaalinen nelikulmio.^[16]

Ortodiagonaalinen nelikulmio

Ortodiagonaalisen nelikulmion lävistäjät leikkaavat toisensa kohtisuorasti. Vaikka neliöllä ja neljäkkäällä on tämä ominaisuus, ei nelikulmion tarvitse olla tasasivuinen tai tasakulmainen. Sen ei tarvitse olla edes konveksi. Kohtisuoruudesta seuraa joitakin erityisiä ominaisuuksia.^[17]

Leija

Leija on symmetrinen yhden lävistäjänsä suhteen. Tällöin symmetrialävistäjä jakaa nelikulmion kahteen yhtenevään kolmioon, joiden kaikki vastinosat ovat keskenään samat. Lävistäjä myös puolittaa kärkiensä kulmat.^[18]

Ominaisuuksia

Pinta-ala

Yksinkertaisen nelikulmion, eli sekä konveksin että konkaavin, pinta-ala lasketaan kaavalla

A={\tfrac {1}{2}}d_{1}d_{2}\;\sin \,\varphi =m_{1}m_{2}\sin \epsilon

^[19]^[20]^[11]

jossa d₁ ja d₂ ovat sen lävistäjät, $\varphi$ on lävistäjien välinen kulma, m₁ ja m₂ ovat bimediaaneja ja $\epsilon$ on bimediaanien välinen kulma.

Toinen tapa laskea pinta-ala on, kun $s={\tfrac {1}{2}}(a+b+c+d)$ on puolipiiri,

A={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}{\tfrac {\beta +\delta }{2}}}}.

^[21]

Muita kaavoja pinta-alalle ovat^[22]

A={\frac {1}{4}}(b^{2}+d^{2}-a^{2}-c^{2})\tan \varphi

ja

A={\frac {1}{4}}{\sqrt {4d_{1}^{2}d_{2}^{2}-(b^{2}+d^{2}-a^{2}-c^{2})^{2}}}

Katso myös

Neliöluku

Lähteet

Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
Alatupa, Sami et al.: Pitkä Sigma 3. (lukion pitkän matematiikan oppikirja) Helsinki: Otava, 2008. ISBN 978-951-26-5927-2
Kontkanen, Pekka & al.: Pyramidi 3. (lukion pitkän matematiikan oppikirja) Helsinki: Tammi, 2005. ISBN 978-951-26-5059-0

Viitteet

↑ ^a ^b ^c ^d ^e ^f Väisälä, Kalle: Geometria, s. 22–25.
↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Alatupa, Sami et al.: Pitkä Sigma 3 – Geometria, 2008, s. 17–27.
↑ ^a ^b ^c ^d Kontkanen, Pekka et al.: Pyramidi 3 – Geometria, 2005, s. 25–27.
↑ ^a ^b ^c Weisstein, Eric W.: Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
↑ ^a ^b de Villiers, Michael: Stars: A Second Look (Arkistoitu – Internet Archive), Mathematics in School 28(5), 11/1999
↑ ^a ^b Kivinen, s. Albert: Analyysin paradoksi (Arkistoitu – Internet Archive), Tieteessä tapahtuu
↑ Math Open Reference: Interior Angles of a Polygon
↑ ^a ^b ^c ^d Kontkanen, Pekka et al.: Pyramidi 3 – Geometria, 2005, s. 44–52.
↑ ^a ^b ^c ^d ^e Väisälä, Kalle: Geometria, s. 70–71.
↑ Väisälä, Kalle: Geometria, s. 91–93.
↑ ^a ^b Seppänen, Raimo et al.: MAOL-taulukot, s. 29–30. Helsinki: Kustannusosakeyhtiö Otava, 1991. ISBN 951-1-16053-2
↑ Väisälä, Kalle: Geometria, s. 84–90.
↑ Weisstein, Eric W.: Cyclic Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
↑ Weisstein, Eric W.: Tangential Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
↑ http://forumgeom.fau.edu/FG2011volume11/FG201108.pdf (Arkistoitu – Internet Archive)
↑ Weisstein, Eric W.: Bicentric Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
↑ Josefsson, Martin: Characterizations of Orthodiagonal Quadrilaterals. Forum Geometricorum, 2012, nro 12, s. 13–25. ISSN 1534-1178 Artikkelin verkkoversio. (pdf) Viitattu 15.10.2013. (englanniksi) (Arkistoitu – Internet Archive)
↑ Keranto, Tapio: Tulevien opettajien tasogeometrisen tiedon ja päätelmien tasosta: tapauksena nelikulmiohierarkia ja eräät muut tasogeometriset objektit, s. 95–110. (julkaisussa MATEMATIIKAN JA LUONNONTIETEIDEN OPETUKSEN TUTKIMUSPÄIVÄT OULUSSA 25.–26.11.2004) Oulu: Oulun yliopisto, 2005. ISBN 951-42-7887-9 Teoksen verkkoversio (pdf) (viitattu 31.10.2013).
↑ Harries J.: Area of a Quadrilateral. The Mathematical Gazette, 2002, 86. vsk, nro 506, s. 310-311. Lontoo, Englanti: The Mathematical Association. ISSN 0025-5572 Artikkelin verkkoversio. (pdf) (englanniksi)
↑ Josefsson, Martin: Five Proofs of an Area Characterization of Rectangles. Forum Geometricorum, 2013, nro 13, s. 17–21. Florida Atlantic University. ISSN 1534-1178 Artikkelin verkkoversio. (pdf) (englanniksi) (Arkistoitu – Internet Archive)
↑ Yiu, P.: Euclidean Geometry (luentomoniste, s.147–148) Geometry. 1998. Florida Atlantic University. Arkistoitu 2.3.2019. Viitattu 25.9.2013.
↑ Lennart Råde, Bertil Westergren: Mathematics Handbook for Science and Engineering

Aiheesta muualla

van Tienhoven, Chris: Encyclopedia of Quadri-Figures
de Villiers, Michael: The role and function of a hierarchical classification of quadrilaterals (Arkistoitu – Internet Archive)

[vaisala22-1] ↑ ^a ^b ^c ^d ^e ^f Väisälä, Kalle: Geometria, s. 22–25.

[ala3_17-2] ↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Alatupa, Sami et al.: Pitkä Sigma 3 – Geometria, 2008, s. 17–27.

[kon3_25-3] Kontkanen, Pekka et al.: Pyramidi 3 – Geometria, 2005, s. 25–27.

[Quadrilateral-4] Weisstein, Eric W.: Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[second-5] Villiers, Michael: Stars: A Second Look (Arkistoitu – Internet Archive), Mathematics in School 28(5), 11/1999

[kivi-6] Kivinen, s. Albert: Analyysin paradoksi (Arkistoitu – Internet Archive), Tieteessä tapahtuu

[iap-7] Math Open Reference: Interior Angles of a Polygon

[kon3_44-8] Kontkanen, Pekka et al.: Pyramidi 3 – Geometria, 2005, s. 44–52.

[vaisala70-9] Väisälä, Kalle: Geometria, s. 70–71.

[vaisala91-10] Väisälä, Kalle: Geometria, s. 91–93.

[maol-11] Seppänen, Raimo et al.: MAOL-taulukot, s. 29–30. Helsinki: Kustannusosakeyhtiö Otava, 1991. ISBN 951-1-16053-2

[vaisala84-12] Väisälä, Kalle: Geometria, s. 84–90.

[CyclicQuadrilateral-13] Weisstein, Eric W.: Cyclic Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[TangentialQuadrilateral-14] Weisstein, Eric W.: Tangential Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[15] ttp://forumgeom.fau.edu/FG2011volume11/FG201108.pdf (Arkistoitu – Internet Archive)

[BicentricQuadrilateral-16] Weisstein, Eric W.: Bicentric Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[ortodia-17] Josefsson, Martin: Characterizations of Orthodiagonal Quadrilaterals. Forum Geometricorum, 2012, nro 12, s. 13–25. ISSN 1534-1178 Artikkelin verkkoversio. (pdf) Viitattu 15.10.2013. (englanniksi) (Arkistoitu – Internet Archive)

[herkules-18] Keranto, Tapio: Tulevien opettajien tasogeometrisen tiedon ja päätelmien tasosta: tapauksena nelikulmiohierarkia ja eräät muut tasogeometriset objektit, s. 95–110. (julkaisussa MATEMATIIKAN JA LUONNONTIETEIDEN OPETUKSEN TUTKIMUSPÄIVÄT OULUSSA 25.–26.11.2004) Oulu: Oulun yliopisto, 2005. ISBN 951-42-7887-9 Teoksen verkkoversio (pdf) (viitattu 31.10.2013).

[harries-19] Harries J.: Area of a Quadrilateral. The Mathematical Gazette, 2002, 86. vsk, nro 506, s. 310-311. Lontoo, Englanti: The Mathematical Association. ISSN 0025-5572 Artikkelin verkkoversio. (pdf) (englanniksi)

[mj5-20] Josefsson, Martin: Five Proofs of an Area Characterization of Rectangles. Forum Geometricorum, 2013, nro 13, s. 17–21. Florida Atlantic University. ISSN 1534-1178 Artikkelin verkkoversio. (pdf) (englanniksi) (Arkistoitu – Internet Archive)

[yiu147-21] Yiu, P.: Euclidean Geometry (luentomoniste, s.147–148) Geometry. 1998. Florida Atlantic University. Arkistoitu 2.3.2019. Viitattu 25.9.2013.

[22] Lennart Råde, Bertil Westergren: Mathematics Handbook for Science and Engineering

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

Nelikulmio

Sisällys

Nelikulmioiden luokittelu

Kompleksinen nelikulmio