Tasasivuinen monikulmio

Murtoviiva, jossa jokainen jana yhtä pitkä. Yhdistämällä vapaat päätepisteet toisinsa ja asemoimalla janoja eri asentoihin voidaan muodostaa erilaisia tasasivuisia monikulmia.

Tasasivuinen monikulmio on monikulmio, jonka kaikki sivut ovat yhtä pitkiä. Jos tasasivuisessa monikulmiossa ovat lisäksi kaikki kulmat yhtä suuret, kyseessä on säännöllinen monikulmio.

Tasasivuisen monikulmion voidaan ajatella syntyneet sellaisen murtoviivan sulkeutumisesta, jossa janat ovat tasamittaisia. Koska kulmat voidaan määrittää melko vapaasti, voi monikulmiosta tulla esimerkiksi itseään leikkaava, tähti, konkaavi tai konveksi.

Tasasivuinen monikulmio perii kaikki yleisen monikulmion ominaisuudet. Esimerkiksi konveksilla n-kulmiolla, jossa on siis n kappaletta kulmia, kaikkien kulmien summa on (n - 2)·180°. Mutta sivujen pituudet ovat kaikilla sama s, joten piirin pituus p on kaikilla n-kulmioilla sama p = n·s.

Esimerkkejä

Murtoviiva, jossa on vain yksi tai kaksi janaa, ei muodosta monikulmiota. Kun murtoviivassa on kolme tai enemmän janoja, saadaan niistä vaihteleva määrä monikulmioita. Seuraavat esimerkit ovat yksinkertaisimpia.

Kolmikulmio

Kolmijanaisesta murtoviivasta voidaan muodostaa kolmio yhdellä ainoalla tavalla. Tasasivuisessa kolmiossa on kolme yhtä pitkää sivua, mutta rakenteen ainutlaatuisuuden vuoksi kulmatkin ovat yhtä suuret. Kuvio on samalla säännöllinen.

• 
  Tasasivuinen kolmio
• 
  Neljäkäs
• 
  Neliö

Nelikulmio

Tasasivuiset nelikulmiot ovat kaikki konvekseja monikulmioita. Niitä kutsutaan neljäkkäiksi, jonka kulmat voivat vaihdella $0<\alpha <180^{\circ }$. Neljäkäs on suunnikas, sillä vastaiset sivut ovat aina yhdensuuntaiset. Kun yksikin kulma on suora, muuttuu neljäkäs neliöksi, jossa kaikki kulmat ovat suoria ja nelikulmio säännöllinen.

Viisikulmio

Jaottelu, kun $\alpha \geq \beta \geq \delta$. Ylhäällä itseään leikkaava tai tähti, keskellä konkaavi ja alhaalla konveksi. Muualla epäsäännöllisempi.

Tasasivuisella viisikulmiolla löytyy erilaisia muotoja melko paljon. Säännöllisen viisikulmion kaikki kulmat ovat 108^o. Se on konveksi viisikulmio, joka muuttuu konkaaviksi, kun yksi tai kulmaa oikenevat kuperiksi kulmiksi eli yli 180^o:ksi. Jos kuperat kulmat aukeavat lisää ja yksi sivu koskettaa kuperaa kärkeä, muuttuu kuvio kaksiosaiseksi. Nyt kuvion voi taivuttaa itseään risteäväksi. Tällöin viisikulmiolla on kaksi sisäosaa kuin epäsäännöllisellä perhosella. Säännöllisin itseään risteävä muoto on säännöllinen tähti, jota kutsutaan pentagrammiksi.

• 
  Tasasivuinen viisikulmio
• 
  Jako osakolmioihin
• 
  Säännöllinen viisikulmio
• 
  Pentagrammi

Kuusikulmio

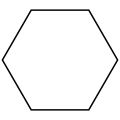
Säännöllinen kuusikulmio esiintyy luonnossa yleisesti siellä, minne geometrisesti järjestäytyneitä rakenteita kehittyy. Siinä ovat sekä kulmat että sivut kaikki yhtä suuria. Kun kulmia aletaan varioida, syntyy erilaisia konvekseja monikulmioita, mutta kun yksikin kulma taipuu kuperaksi, muuttuu kuvio konkaaviksi.

• 
  Säännöllinen kuusikulmio
• 
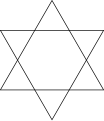
  Heksagrammi ei ole tasasivuinen kuusikulmio, vaan kaksi tasasivuista kolmiota.