Bravais’n hila

Bravais’n hila on geometriassa ja kristallografiassa ääretön pistejoukko, jonka muodostavat ne avaruuden pisteet, joiden paikkavektorit kolmiulotteisessa avaruudessa ovat muotoa

\mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}+n_{3}\mathbf {a} _{3}

missä a₁, a₂ ja a₃ ovat kolme erisuuntaista, lineaarisesti riippumatonta vektoria ja n₁, n₂ ja n₃ mielivaltaisia kokonaislukuja. Tällaisten pisteiden paikkavektorien joukko on suljettu vektorien yhteen- ja vähennyslaskun suhteen, toisin sanoen kahden tähän joukkoon kuuluvan vektorin summa ja erotus kuuluvat myös tähän joukkoon. Bravais’n hila on saanut nimensä ranskalaisen fyysikko Auguste Bravais’n (1811–1863) mukaan, joka vuonna 1850 todisti, että on olemassa 14 mahdollista kidehilatyyppiä.^[1]

Bravais’n hila on translaatiosymmetrinen sellaisten yhdensuuntaissiirtojen suhteen, joiden siirtymävektori vastaa jonkin siihen kuuluvan pisteen paikkavektoria. Toisin sanoen jos hilassa siirrytään toiseen paikkaan tällaisen siirtymävektorin osoittamalla tavalla, sen pisteen ympäristö, johon päädytään, on samanlainen kuin lähtöpisteenkin.

Bravais’n hilan käsite voidaan siis määritellä puhtaan geometrisesti, mutta sen tärkeimmät sovellukset liittyvät kiinteiden aineiden kidehilojen tutkimukseen eli kristallografiaan. Tällöin hilapisteet vastaavat atomien, ionien tai polymeeriketjujen sijaintia aineen kidehilassa. Kiteessä nämä sijaitsevat säännöllisessä järjestyksessä, niin että monessa tapauksessa atomien tai ionien sijaintipaikat muodostavat Bravais’n hilan. Tosin on huomattava, että geometrinen Bravais’n hila jatkuu joka suunnassa äärettömän kauas, kun taas kidehila käsittää vain rajallisen alueen, jota rajoittavat kiteen rajapinnat. Kun kiteen läpimitta kuitenkin tyypillisesti on tuhansia tai jopa miljoonia kertoja suurempi kuin atomien välinen etäisyys, valtaosa kiteen atomeista sijaitsee sen sisällä ja vain pieni osa kokonaismäärästä rajapinnalla.

Kahta Bravais’n hilaa pidetään yleensä ekvivalentteina, jos niillä on isomorfiset symmetriaryhmät. Tässä mielessä kolmiulotteisessa avaruudessa on 14 erilaista Bravais’n hilaa. Nämä 14 mahdollista Bravais’n hilaa muodostavat osajoukon 230 avaruusryhmästä.

Kahdessa ulottuvuudessa

Kaksiulotteiset Bravais’n hilat: 1 – vinoasentoinen (monokliininen), 2 – suorakulmainen (ortorombinen), 3 – suorakulmainen keskinen (ortorombinen), 4 – heksagonaalinen, 5 – neliömäinen (tetragonaalinen).

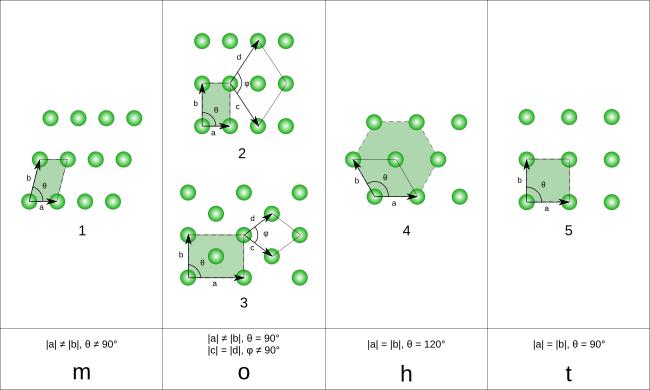
Kaksiulotteisessa avaruudessa on viisi erilaista Bravais’n hilaa,^[2], jotka voidaan ryhmitellä neljään kideperheeseen.

Kideperhe	Schoenfliesin merkintä	Bravais’n hila
Kideperhe	Schoenfliesin merkintä	Yksinkertainen	Keskinen
Monokliininen	C₂	vinoasentoinen
Ortorombinen	D₂	Suorakulmainen	keskinen
Heksagonaalinen	D₆	Heksagonaalinen
Tetragonaalinen	D₄	Neliömäinen

Yksikkökopit määräytyvät koppien sivujen suhteellisten pituuksien (a ja b) sekä niiden välisen kulman ( $\theta$ mukaan. Yksikkökopin pinta-ala voidaan laskea sivuja vastaavien vektorien a ja b eli hilavektorien ristitulon avulla:

A=|{\vec {a}}\times {\vec {b}}|

,

Keskinen suorakulmainen Bravais’n hila eroaa yksinkertaisesta suorakulmaisesta vain siinä, että siinä on hilapiste, paitsi suorakulmion kärjissä, myös sen keskipisteessä. Voisi olettaa, että vastaavalla tavalla muistakin hiloista voitaisiin johtaa uusi hilatyyppi. Kuitenkin jos neliölliseen hilaan lisätään hilapisteet neliöiden keskipisteisiin, saadaan vain toinen neliöllinen hila, jonka hilavektorit ovat alkuperäisiin nähden 45 asteen kulmassa. Jos taas monokliiniseen hilaan lisätään hilapisteet suunnikkaan muotoisten yksikkökoppien keskipisteisiin, saadaan jälleen monokliininen hila, jossa vain toinen hilavektoreista sekä hilavektorien välinen kulma poikkeavat alkuperäisistä. Jos taas heksagonisen hilan yksikkökoppien keskipisteisiin lisätään hilapisteet, saadaan yksinkertainen suorakulmainen hila, jonka hilavektorien suunnat poikkeavat alkuperäisen hilasta.

Seuraavassa taulukossa luetellaan kideperheiden ominaisuuksia:

Kideperhe	Yksikkökopin pinta-ala	Sivujen pituudet	Sivujen välinen kulma
Monokliininen	$ab\,\sin \theta$	a ≠ b	θ ≠ 90°
Ortorombinen	$ab$	a ≠ b	θ = 90°
Heksagonaalinen	${\frac {\sqrt {3}}{2}}\,a^{2}$	a = b	θ = 120°
Tetragonaalinen	$a^{2}$	a = b	θ = 90°

Kolmessa ulottuvuudessa

Kolmiulotteisessa avaruudessa on 14 Bravais’n hilaa. Ne saadaan yhdistämällä kuhunkin seitsemästä kidejärjestelmästä yksi keskisyystyypeistä. Keskisyystyypit osoittavat hilapisteiden paikat yksikkökopissa seuraavasti:

Yksinkertainen eli primitiivinen (P): hilapisteitä on vain kopin kärkipisteissä
Pohjakeskiset (A, B tai C): hilapisteet on yksikkökopin kärjissä sekä lisäksi tietyn suuntaisten sivutahkojen keskipisteissä.
Tilakeskinen (I): hilapisteet ovat yksikkökopin kärjissä sekä lisäksi kopin keskipisteessä
Pintakeskinen (F): hilapisteet ovat yksikkökopin kärjissä sekä lisäksi sen kaikkien sivutahkojen keskipisteissä

Kaikkia kidejärjestelmän ja keskisyystyypin yhdistelmiä ei kuitenkaan tarvita kuvaamaan kaikkia mahdollisia hiloja, sillä osoittautuu, että jotkin niistä ovat ekvivalentteja toistensa kanssa. Esimerkiksi monokliinin tilakeskinen hila voidaan kuvata myös monokliinisenä pohjakeskisenä hilana valitsemalla kiteen akselit toisin. Samoin kaikki pohjakeskiset A- ja B-hilat voidaan kuvata joko C-hilana tai yksinkertaisena hilana. Tämä vähentää yhdistelmien lukumäärän neljääntoista, jotka esitetään seuraavassa taulukossa:^[3]

Kideperhe	Hilajärjestelmä	Schoenfliesin merkintä	14 Bravais’n hilaa
Kideperhe	Hilajärjestelmä	Schoenfliesin merkintä	Yksinkertainen (P)	Pohjakeskinen (C)	Tilakeskinen (I)	Pintakeskinen (F)
Trikliininen		C_i
Monokliininen		C_2h
Ortorombinen		D_2h
Tetragonaalinen		D_4h
Heksagonaalinen	Romboedrinen	D_3d
Heksagonaalinen	Heksagonaalinen	D_6h
Kuutiollinen		O_h

Tarkemmin yksikkökopit voidaan kuvailla kopin särmien suhteellisten pituuksien (a, b, c) ja niiden välisten kulmien (α, β, γ) avulla. Yksikkökopin tilavuus voidaan laskea skalaarikolmitulon a · (b × c), avulla, missä a, b ja c ovat hilavektorit. Kidejärjestelmien ominaisuuksia on lueteltu seuraavassa taulukossa:

Kideperhe	Hilajärjestelmä	Tilavuus	Aksiaaliset etäisyydet (särmien pituudet)^[4]	Akselien väliset kulmat^[4]	Esimerkkejä
Trikliininen		$abc{\sqrt {1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$	(muut kuin jäljempänä esitettävät tapaukset)		K₂Cr₂O₇, CuSO₄·5H₂O, H₃BO₃
Monokliininen		$abc\,\sin \beta$	a ≠ c	α = γ = 90°, β ≠ 90°	Monokliininen rikki, Na₂SO₄·10H₂O, PbCrO₃
Ortorombinen		$abc$	a ≠ b ≠ c	α = β = γ = 90°	rombinen rikki, KNO₃, BaSO₄
Tetragonaalinen		$a^{2}c$	a = b ≠ c	α = β = γ = 90°	Valkoinen tina, SnO₂, TiO₂, CaSO₄
Heksagonaalinen	Romboedrinen	$a^{3}{\sqrt {1-3\cos ^{2}\alpha +2\cos ^{3}\alpha }}$	a = b = c	α = β = γ ≠ 90°	Kalsiitti (CaCO₃), sinooperi (HgS)
Heksagonaalinen	Heksagonaalinen	${\frac {\sqrt {3}}{2}}\,a^{2}c$	a = b	α = β = 90°, γ = 120°	Grafiitti, ZnO, CdS
Kuutiollinen		$a^{3}$	a = b = c	α = β = γ = 90°	NaCl, KCl, sinkkivälke, kupari, hopea

Hiloja, jotka eivät ole Bravais’n hiloja

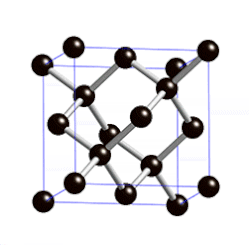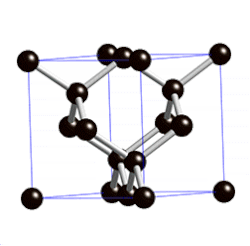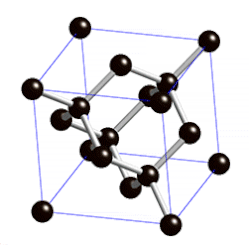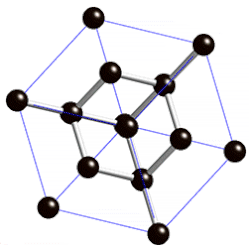
On olemassa myös kidehiloja, jotka eivät ole Bravais’n hiloja. Sellainen on esimerkiksi heksagonaalinen tiivispakkaus (HCP). Se muodostuu tosin heksagonaalisista yksikkökopeista, joissa hilavektorien välinen kulma on 60°, mutta kussakin tällaisessa yksikkökopissa on kaksi hilapistettä. Jos yksikkökopin korkeutta merkitään h:lla, tasoilla z=nh, missä n on mielivaltainen kokonaisluku, hilapisteet ovat samoilla kohdilla eli kullakin tasolla niillä on samat x- ja y-koordinaatit, mutta tasoilla z = (n+1/2)h nämä koordinaatit ovat toiset. Jos a jokin tasolla z=h/2 olevan hilapisteen paikkavektori, ei piste 2a ole hilapiste ja näin ollen hila ei määritelmän mukaan ole Bravais’n hila. Tasolla z=h/2 olevat hilapisteet muodostavat kylläkin samanlaisen tasasivuisista kolmioista muodostuvan verkoston kuin tasolla z=0 olevatkin, mutta näiden pisteiden kolmiulotteiset lähiympäristöt ovat päinvastaisilla tavoilla suuntautuneet. Jos kuitenkin otetaan huomioon vain joka toisella hilatasolla olevat hilapisteet, ne muodostavat heksagonaalisen Bravais’n hilan.^[5]

Myöskään timanttirakenteinen hila ei ole Bravais’n hila. Sen yksikkökoppi on kuutio 0<=x<d, 0<=y<d, 0<=z<d, jossa hilapisteitä ovat (0,0,0), (0,d/2,d/2), (d/2,0,d/2), (d/2,d/2,0), (d/4,d/4,d/4), (d/4, 3d/4, 3d/4), (3d/4 ,d/4, 3d3/4) ja (3d/4, 3d/4, d/4). Piste a=(d/4,d/4,d/4) on siis hilapiste, mutta piste 2a = (1/2,1/2,1/2) ei ole, eikä kyseessä siis ole Bravais’n hila. Jos kuitenkin otetaan huomioon edellä olevista hilapisteistä vain ne, joiden koordinaateissa ei ole nimittäjää 4, ne muodostavat pintakeskeisen kuutiollisen Bravais’n hilan. Toisaalta ne hilapisteet, joiden koordinaateissa esiintyy nimittäjä 4, muodostavat nekin pintakeskeisen kuutiollisen hilan, joka kuitenkin on päinvastaisella tavalla suuntautunut.^[5]

Neljässä ulottuvuudessa

Matemaattisesti Bravais’n hilan käsite voidaan yleistää myös neljään tai useampaan ulottuvuuteen. Voidaan osoittaa, että neljässä ulottuvuudessa on 64 Bravais’n hilaa, joista 23 on yksinkertaisia ja 41 keskisiä. Kymmenen Bravais’n hilaa jakautuu enantiomorfisiin pareihin, jotka ovat toistensa peilikuvia.^[6]

Katso myös

Lähteet

↑ Malcolm E. Lines: ”Aristoteleesta lasin rakenteeseen”, Jättiläisen harteilla: Matematiikan heijastuksia luonnontieteeseen, s. 25. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X
↑ Charles Kittel: Introduction to Solid State Physics, s. 10. New York: John Wiley & Sons. ISBN 0-471-11181-3 Teoksen verkkoversio.
↑ Theo Hahn: International Tables for Crystallography, Volume A: Space Group Symmetry, s. 744. Springer-Verlag, 2002. doi:10.1107/97809553602060000100 ISBN 978-0-7923-6590-7
↑ ^a ^b Theo Hahn: International Tables for Crystallography, Volume A: Space Group Symmetry, s. 758. Springer-Verlag, 2002. doi:10.1107/97809553602060000100 ISBN 978-0-7923-6590-7
↑ ^a ^b H. E. Hall: ”Typical crystal structures”, Solid state physics, s. 34–40. John Wiley & Sons Ltd, 1979. ISBN 0-471-34280-7
↑ Harold Brown, Rolf Bülow, Joachim Neubüser, Hans Wondratschek, Hans Zassenhaus: Crystallographic groups of four-dimensional spae. New York: Wiley-Interscience [John Wiley & Sons], 1978. ISBN 978-0-471-03095-9

Käännös suomeksi

Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Bravais lattice

[Lines-1] Malcolm E. Lines: ”Aristoteleesta lasin rakenteeseen”, Jättiläisen harteilla: Matematiikan heijastuksia luonnontieteeseen, s. 25. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X

[2] Charles Kittel: Introduction to Solid State Physics, s. 10. New York: John Wiley & Sons. ISBN 0-471-11181-3 Teoksen verkkoversio.

[3] Theo Hahn: International Tables for Crystallography, Volume A: Space Group Symmetry, s. 744. Springer-Verlag, 2002. doi:10.1107/97809553602060000100 ISBN 978-0-7923-6590-7

[axial_dimensions-4] Theo Hahn: International Tables for Crystallography, Volume A: Space Group Symmetry, s. 758. Springer-Verlag, 2002. doi:10.1107/97809553602060000100 ISBN 978-0-7923-6590-7

[Hall34-5] H. E. Hall: ”Typical crystal structures”, Solid state physics, s. 34–40. John Wiley & Sons Ltd, 1979. ISBN 0-471-34280-7

[6] Harold Brown, Rolf Bülow, Joachim Neubüser, Hans Wondratschek, Hans Zassenhaus: Crystallographic groups of four-dimensional spae. New York: Wiley-Interscience [John Wiley & Sons], 1978. ISBN 978-0-471-03095-9

[1]

[2]

[3]

[4]

[5]

[6]

Bravais’n hila

Sisällys

Kahdessa ulottuvuudessa

Kolmessa ulottuvuudessa

Hiloja, jotka eivät ole Bravais’n hiloja

Neljässä ulottuvuudessa

Katso myös

Lähteet

Navigointivalikko

Bravais’n hila

Kahdessa ulottuvuudessa

Kolmessa ulottuvuudessa

Hiloja, jotka eivät ole Bravais’n hiloja

Neljässä ulottuvuudessa

Katso myös

Lähteet

Navigointivalikko

Haku