Penrosen laatat

Penrosen laattoja.

Penrosen laatat ovat tapa peittää taso jaksottomasti pienellä joukolla erilaisia monikulmioita. Ne ovat saaneet nimensä tällaisia laatoituksia 1970-luvulla tutkineen matemaatikko Roger Penrosen mukaan.

Jaksottomalla peittämisellä tarkoitetaan sitä, ettei minkään samanlaisen pienen laattaryhmän suurempi ympäristö ole missään muualla aivan samanlainen vertailukohtansa kanssa. Toinen tapa havainnollistaa jaksottomuutta on piirtää alueen yli satunnaisesti asemoitu suora ja todeta suoralla olevia laattoja tarkastelemalla, ettei siinä esiinny toistamiseen samaa kuviota missään kohtaa suoraa.

Taso voidaan peittää Penrosen laatoilla monilla tavoilla. Kaikki tällaiset tavat ovat jaksottomia, mutta ne saattavat olla symmetrisiä jonkin akselin suhteen tai niillä voi olla viisinkertainen rotaatiosymmetria, kuten oheisessa kuvassa. Jaksottomuus merkitsee sitä, että Penrosen laatoituksella ei ole siirtosymmetriaa. Toisin sanoen tasolta ei voida valita kahta sellaista kohtaa, että kummastakin mitattuna olisi aina samalla etäisyydellä ja samassa suunnassa saman­laiset ja samassa asennossa olevat laatat. Penrosen laattoja voidaan pitää kvasikiteen kaksi­ulotteisena vastineena.

Tausta ja historia

Penrosen laatat ovat yksinkertaisimpia esimerkkejä tason jakamisesta osiin epäjaksollisesti. Yleisesti laatoituksella tarkoitetaan tason jakoa osiin, jotka eivät osittainkaan peitä toisiansa eivätkä jätä väliinsä aukkoja. Yleensä edellytetään myös, että käytetään vain äärellistä määrää erilaisia muotoja. Tunnetuimmat laatoitukset, esimerkiksi tason jako neliöiksi tai tasa­sivuisiksi kolmioiksi, ovat jaksollisia. Toisin sanoen on olemassa sellainen etäisyys, jonka verran tiettyyn suuntaan siirryttäessä laatoitus toistuu aina samanlaisena. Tätä etäisyyttä sanotaan laatoituksen jaksoksi. Jos tällaista jaksoa ei ole, laatoitusta sanotaan jaksottomaksi.

Wangin dominot muodostavat jaksottoman laatoituksen.

Kysymys jaksottomista laatoituksista sai osakseen uutta mielenkiintoa 1960-luvulla, kun loogikko Hao Wang havaitsi yhteyden niiden ja päätöksenteko-ongelmien kanssa. Hän käsitteli erityisesti neliömäsiä laattoja, joiden sivut olivat väritettyjä. Tällaisia sanotaan nykyään Wangin dominoiksi. Wang esitti kysymyksen: "Millä edellytyksellä taso voidaan peittää annetulla joukolla tällaisia laattoja siten, että vierekkäisten laattojen samanväriset reunat aina koskettavat toisiaan?" Hän osoitti, että jos ongelmaa ei voida ratkaista rekursiivisesti, on olemassa keino peittää taso jaksottomasti Wangin dominoilla. Tuohon aikaan tämä vaikutti kuitenkin epäuskottavalta, minkä vuoksi Wang esitti konjektuurin, ettei sellainen laatoitus ole mahdollinen.

Robinsonin kuusi laattaa.

Wangin oppilas Robert Berger todisti kuitenkin väitöskirjassaan vuonna 1964, että ongelmaa ei voitu ratkaista rekursiivisesti, joten Wangin konjektuuri on epätosi. Hän pystyikin muodostamaan jaksottoman laatoituksen 20426 Wangin dominosta. Myöhemmin hän osoitti, että siihen riitti 104 sellaista laattaa. Vuonna 1968 Donald Knuth osoitti, että 92 laattaakin riittää. Alkuperäisissä Wangin dominoissa ehtona oli, että Wangin dominoiden vierekkäisissä laatoissa samanväristen sivujen on kosketettava toisiaan. Tämä ehto voidaan myös korvata oletuksella, että laattojen reunat ovat eri tavoin kaarevia tavallisten palapelin palojen tapaan. Vuonna 1971 Raphael Robinson osoitti tällä tavoin eräässä tutkielmassaan, että jo kuudesta erimuotoisesta laatasta voidaan muodostaa jaksoton laatoitus.

Viisikulmainen Penrosen laatoitus (P1) mustin laatoin, taustalla värillisten suunnikaslaattojen muodostama laatoitus (P3).

Ensimmäinen Penrosen laatoitus, jonka Roger Penrose esitti vuonna 1974 (P1 alla olevassa kuvassa), on myös jaksoton ja muodostuu kuudesta eri muotoisesta laatasta. Se ei muodostu neliöistä, vaan erilaisista viisikulmioista. Säännöllisillä viisi­kulmioilla ei koko tasoa voi peittää jättämättä väliin aukkoja, mutta jo vuonna 1619 Johannes Kepler osoitti teoksessaan Harmonices Mundi, että nämä aukot voidaan täyttää penta­grammeilla, kymmenkulmioilla tai niitä muistuttavilla moni­kulmioilla. Penrose kehitti tätä ajatusta osoittamalla, että tällä tavoin laatoitus voitiin muodostaa jaksottomaksi, mikä täydensi Keplerin äärellisen Aa-mallin. Tähän hän sai vaikutteita myös eräistä Albert Dürerin teoksista.

Myöhemmin Penrose osoitti, että erilaisten laattojen lukumäärä voitiin vähentää kahteen, jolloin saatiin kaksi erilaista laatoitusta P2 ja P3 alla olevassa kuvassa. Näistä jälkimmäisen, suunnikkaista muodostuvan laatoituksen, keksi hänestä riippumatta Robert Ammann vuonna 1976. Penrose ja John H. Conway tutkivat tällaisten laatoitusten ominaisuuksia, ja heidän tutkimustuloksensa julkaisi Martin Gardner tammikuun 1977 Scientific American-lehdessä Mathematical Games-palstalla.

Penrosen laatat

Penrosen alkuperäisistä kuudesta peruslaatasta muodostettu laatoitus.

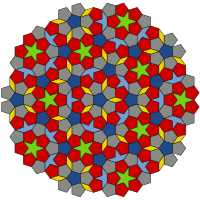
Erityyppiset Penrosen laatat, P1–P3, on jäljempänä kuvattu kukin erikseen, mutta niillä on joukko yhtäläisyyksiä. Kaikissa laatat on muodostettu osista, joista voidaan muodostaa myös säännöllinen viisikulmio, minkä vuoksi niihin liittyy läheisesti kultainen leikkaus. Lisäksi nämä laatoitukset voidaan kukin konstruoida toistensa avulla.

Alkuperäiset Penrosen laatat (P1)

Alkuperäinen Penrosen laatoitus muodostuu viisikulmiosta sekä kolmenlaisista muista erimuotoisista laatoista: viisi­sarakaraisista tähdistä (penta­grammeista), ”veneistä” sekä ”timanteista” eli ohuista suunnikkaista. Sen varmistamiseksi, että laatoituksesta tulee jaksoton, käytettiin tiettyjä sääntöjä sille, miten erilaiset laatat saavat koskettaa toisiaan. Eri viisikulmioille on kolme eri sääntöä ja tällöin eri sääntöjä noudattavat viisikulmiot voidaan tehdä erivärisiksi, kuten oheisessa kuvassa.

Leija- ja nuolilaatat (P2)

Leija- ja nuolilaatat

Penrosen toinen laatoitus koostuu kahdenlaisista nelikulmioista, joita nimitetään leijoiksi ja nuoliksi. Nämä voidaan yhdistää suorakulmioksi, mutta käytettyjen sääntöjen mukaan niin ei saa tehdä, sillä suunnikkaista muodostettu laatoitus olisi jaksollinen. Sekä leija että nuoli voidaan toisaalta käsittää muodostetuksi kahdesta kolmiosta, joita sanotaan Robinsonin kolmioiksi niitä vuonna 1975 tutkineen Robinsonin mukaan.

• "Leija" on nelikulmio, jonka kulmista kolme on 72 ja neljäs 144 asteen suuruinen. Sillä on symmetria-akseli, joka jakaa sen kahteen teräväkulmaiseen Robinsonin kolmioon, joiden kulmat ovat 36, 72 ja 72 astetta. Tällainen kolmio tunnetaan myös kultaisena kolmiona.
• "Nuoli" on ei-kupera nelikulmio, jonka sisäpuoliset kulmat ovat 36, 72, 36 ja 216 astetta. Myös sillä on symmetria-akseli, joka jakaa sen kahdeksi tylppäkulmaiseksi Robinsonin kolmioksi, joiden kulmat ovat 36, 36 ja 108 astetta.

Suunnikaslaatat (P3)

Kolmas Penrosen laatoitus muodostuu kahdenlaisista suunnikkaista. Niistä kuitenkin voidaan muodostaa myös jaksollinen laatoitus, minkä vuoksi on noudatettava tiettyjä rajoittavia sääntöjä, jotta tuloksena olisi jaksoton laatoitus.

Penrosen suunnikaslaattojen yhdistelysäännöt ja niihin liittyvät sivujen muutokset.

Laatoituksessa käytetään kahdenlaisia suunnikkaita, jotka molemmat voidaan myös jakaa kahdeksi Robinsonin kolmioksi.

• Ohuessa laatassa t kulmat ovat 36, 144, 36 ja 144 astetta. Sen lyhempi lävistäjä jakaa sen kahdeksi Robinsonin kolmioksi.
• Paksussa laatassa T kulmat ovat 72, 108, 72 ja 108 astetta. Sen pidempi lävistäjä jakaa sen kahdeksi tylppäkulmaiseksi Robinsonin kolmioksi.

Laattojen eri sivut oletetaan kuitenkin erilaisiksi, ja ne sijoitellaan siten, että vierekkäisten laattojen on noudatettava tiettyjä sääntöjä. Nämä säännöt voidaan kuvata eri tavoin, kuten käy ilmi oheisesta kuvasta. Esimerkiksi niiden sivuille merkittyjen kaarien on vastattava toisiaan väriltään ja asennoltaan tai niiden sivuille tehtyjen lovien on sovittava yhteen.

Kaikkiaan näiden laattojen kulmat voidaan asettaa 54 eri tavalla vierekkäin siten, että samassa kärkipisteessä toisensa kohtaavien laattojen väliin ei jää aukkoja. Näistä vain seitsemän tapaa on laatoituksen sääntöjen mukaan sallittuja, joskin yksi niistä voidaan toteuttaa kahdella eri tavalla.

Konstruointi ja ominaisuuksia

Deflaatio

Penrosen leija- ja nuolilaatoitus voidaan yksinkertaisimmin konstruoida deflaatioksi nimitetyllä menetelmällä. Lähtökohdaksi otetaan tietty äärellisen kokoinen laatoitus, jota nimitetään "aksioomaksi", ja siitä muodostetaan tiettyjen sääntöjen mukaan joukko peräkkäisiä laatoituksia, joita nimitetään "sukupolviksi". Yksin­kertaisimmassa tapauksessa "aksiooma" käsittää vain yhden laatan. Siirryttäessä seuraavaan "sukupolveen" jokainen laatta korvataan yhdellä tai useammalla uudella laatalla, jotka peittävät alku­peräisen laatan kokonaan. Täten uudet laatat ovat yhden­muotoisia alkuperäisten kanssa, mutta kooltaan pienempiä. Kun tämä toistetaan riittävän monta kertaa, saadaan lopulta laatoitus, joka sisältää sellaisen osan, joka on yhdenmuotoinen alkuperäisen "aksiooman" kanssa eikä ulotu kuvion reunoille. Tämä valitaan sitten uudeksi "aksioomaksi", ja koko prosessi toistetaan, jolloin saadaan kerta kerralta laajempi laatoitus, kunnes se lopulta peittää koko tason.

Esimerkki: Kolme sukupolvea neljästä aksioomasta

Tämä on esimerkki peräkkäisistä suku­polvista lähdettäessä neljästä erilaisesta "aksioomasta". "Auringon" ja "tähden" tapauksessa alkuperäisen kanssa yhden­muotoinen pienempi laatoitus saadaan jo toisessa sukupolvessa, "auringon" tapauksessa myös kolmannessa.

Nimi	Sukupolvi 0 (aksiooma)	Sukupolvi 1	Sukupolvi 2	Sukupolvi 3
Leijan puolikas
Nuolen puolikas
Aurinko
Tähti

Penrosen laatat ja kultainen leikkaus

Moniin Penrosen laattojen ominaisuuksiin liittyy läheisesti kultainen leikkaus ja sen suhdeluku $\phi ={\frac {1+{\sqrt {5}}}{2}}$ (noin 1,618). Tämä johtuu siitä, että laatoitus on lokaalisti viisinkertaisesti symmetrinen ja säännöllisessä viisikulmiossa halkaisijan ja sivun suhde on φ. Tämä on myös pidemmän ja lyhemmän sivun suhde molemmissa Robinsonin kolmioissa. Tästä seuraa, että leija- ja nuolilaatoissa pidemmän ja lyhyemmän sivun suhde on myös φ, samoin näiden laattojen pinta-alojen suhde, sivun ja lyhemmän lävistäjän suhde ohuessa suunnikaslaatassa sekä pidemmän lävistäjän ja sivun suhde paksussa suunnikaslaatassa.

Deflaatioprosessissa leija jaetaan kahdeksi leijaksi ja yhdeksi nuoleksi, nuoli taas nuoleksi ja leijaksi. Leijojen ja nuolten lukumäärä prosessin n:nnessä suku­polvessa voidaan laskea matriisin n:nnen potenssin avulla:

${\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,$

missä F_n on Fibonaccin lukujonon n:s luku. Nuolten ja leijojen luku­määrien suhde missä tahansa riittävän laajassa Penrosen P2-laatoituksessa on tämän vuoksi lähellä kultaisen leikkauksen suhde­lukua φ. Vastaava tulos pätee myös paksujen ja ohuiden suunnikkaiden luku­määrälle P3-laatoituksessa..

Penrosen laattoja muistuttavia laatoituksia

Kymmenkulmiolaatoitus ja kvasikiteet

Gummeltin kymmenkulmio (vasemmalla) ja sen osittaminen leijoiksi ja nuoliksi katko­viivoilla osoitettuna; oikealla olevissa kuvioissa olevat väritetyt alueet osoittavat, minkä muotoisten alueiden sallitaan Gummeltin mallissa mennä päällekkäin.

Vuonna 1996, saksalainen matemaatikko Petra Gummelt osoitti, että taso voidaan peittää yhtenevillä säännöllisillä kymmen­kulmioilla, jos niiden sallitaan (Penrosen laatoituksesta poiketen) mennä osittain päällekkäin siten, että vain kahden muotoiset vierekkäisille kymmen­kulmioille yhteiset alueet sallitaan. Kymmen­kulmio jaetaan osiin, jotka väritetään tiettyjen sääntöjen mukaan, ja vain värityksen kanssa yhteen sopivien osien eri kymmen­kulmioissa sallitaan mennä päällekkäin. Jos kymmen­kulmio jaetaan tietyllä tavalla "nuoliksi" ja "leijoiksi", kuviointi muuttuu Penrosen laatoituksen P2 kaltaiseksi. Myös laatoitus P3 voidaan muodostaa sijoittamalla paksu suunnikas kymmen­kulmion sisään, jolloin jäljelle jäävä osa peittyy ohuilla suunnikkailla.

Näitä pidetään realistisina malleina sille, miten kvasikiteet kasvavat: osittain päällekkäiset kymmen­kulmiot ovat "kvasi­yksikkö­koppeja", jotka vastaavat tavallisten kiteiden yksikkö­koppeja, ja tällaisissa rakenteissa atomit pyrkivät pakkautumaan mahdollisimman tiheästi.

Roger Penrose Mitchell Institute for Fundamental Physics and Astronomy'n rakennuksessa Texas A&M Universityssä; huoneen lattia on päällystetty Penrosen laatoilla

Käyttö taiteessa

Laatoitusten esteettinen arvo on ollut kauan tunnustettu. Penrosen laatat herättävätkin yhä suurta mielen­kiintoa, joka kohdistuu suurelta osin pikemmkin niiden muodostamaan näkö­vaikutelmaan kuin niiden matemaattisiin ominaisuuksiin. Niiden onkin todettu muistuttavan Lähi-idässä käytettyä girih-koristekuvuointia, ja Peter Lu ja Paul Steinhardt ovat todenneet, että Penrosen laatoituskin esiintyy jo keski­aikaisessa islamilaisessa taiteessa.

Drop Cityn taiteilija Clark Richert käytti Penrosen suunnikkaita eräässä teoksessaan vuonna 1970. Taide­historioitsija Martin Kemp on todennut, että myös Albrecht Dürer on laatinut saman­kaltaisia sommitelmia näistä suunnikkaista.

Lähteet

Alkuperäislähteet

• R. Berger: The undecidability of the domino problem. 66 Memoirs of the American Mathematical Society, 1966. .
• Algebraic theory of Penrose's nonperiodic tilings of the plane, I, II. Indagationes mathematicae, 1981, 43. vsk, nro 1. Artikkelin verkkoversio. (PDF)
• Penrose tilings as coverings of congruent decagons. Geometriae Dedicata, 1996, 62. vsk, nro 1. doi:10.1007/BF00239998
• Role of aesthetics in pure and applied research. Bulletin of the Institute of Mathematics and its Applications, 1974, nro 10.
• Undecidability and nonperiodicity for tilings of the plane, s. 177–190. 12. vskMääritä julkaisija! doi:10.1007/BF01418780
• Metallic Phase with long-range orientational order and no translational symmetry. Physical Review Letters, 1984, 53. vsk. doi:10.1103/PhysRevLett.53.1951
• Proving theorems by pattern recognition II. Bell Systems Technical Journal, 1961, 40. vsk. .

Sekundaarilähteitä

• David Austin: Penrose Tiles Talk Across Miles. Providence: Feature Column, American Mathematical Society, 2005a. Teoksen verkkoversio.
• David Austin: Penrose Tilings Tied up in Ribbons. Providence: Feature Column, American Mathematical Society, 2005b. Teoksen verkkoversio.
• On aperiodic sets of Wang tiles. Lecture Notes in Computer Science, 1997, 1337. vsk. doi:10.1007/BFb0052084
• Martin Gardner: Penrose Tiles to Trapdoor Ciphers. Cambridge University Press, 1997. ISBN 978-0883855218 . (Julkaissut ensin W. H. Freeman, New York (1989), ISBN 978-0716719861.)
  • Kappale 1 (s. 1–18) on uusi painos artikkelista Extraordinary nonperiodic tiling that enriches the theory of tiles. Scientific American, 1977, 236. vsk, nro 1, s. 110–121. .
• C. Godrèche, F. Lançon: A simple example of a non-Pisot tiling with five-fold symmetry. Journal de Physique I, 1992, 2. vsk. doi:10.1051/jp1:1992134 Artikkelin verkkoversio..
• Branko Grünbaum, G.C. Shephard: Tilings and Patterns. New York: W. H. Freeman, 1987. .
• Science in culture: A trick of the tiles. Nature, 2005, 436. vsk. doi:10.1038/436332a .
• Two-dimensional system with a quasi-crystalline ground state. Journal de Physique, 1988, 4. vsk. doi:10.1051/jphys:01988004902024900 Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
• The Gummelt decagon as a 'quasi unit cell'. Acta Crystallographica, 2001, A57. vsk. doi:10.1107/S0108767301007504 Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
• Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture. Science, 2007, 315. vsk, nro 5815. PubMed:17322056 doi:10.1126/science.1135491 Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
• Dürer-Kepler-Penrose: the development of pentagonal tilings. Materials Science and Engineering, 2000, 294. vsk, nro 6.
• Fast Hierarchical Importance Sampling with Blue Noise Properties. ACM Transactions on Graphics, 2004, 23. vsk, nro 3. ACM Press. doi:10.1145/1015706.1015750 Artikkelin verkkoversio.
• ”Fivefold Symmetry”, 800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired, s. 67–86. Singapore–London: World Scientific, 1992.
• Marjorie Senechal: Quasicrystals and geometry. Cambridge University Press, 1996. ISBN 978-0521575416 .
• Paul J. Steinhardt, Hyeong-Chai Jeong: A simpler approach to Penrose tiling with implications for quasicrystal formation. Nature, 1.8.1996, 382. vsk. doi:10.1038/382431a0 Artikkelin verkkoversio..
• Minimal chaos, stochastic web and structures of quasicrystal symmetry. Soviet Physics Uspekhi, 1988, 31. vsk. doi:10.1070/PU1988v031n10ABEH005632
• Philip Ball: Kemian eturintamassa : matka molekyylien maailmaan, s. 165–170. Suomentanut Kimmo Pietiläinen. Terra Cognita, 1997. ISBN 9525202070
• Malcolm E. Lines: Jättiläisen harteilla - matematiikan heijastuksia luonnontieteeseen, s. 114–117. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X

Aiheesta muualla

• John Savard: Penrose Tilings quadibloc.com.
• Eric Hwang: Penrose Tiling intendo.net.
• E. Harriss and D. Frettlöh: Penrose Rhomb Tilings Encyclopedia. Department of Mathematics, University of Bielefeld. Arkistoitu 6.1.2010.
• Kevin Brown: On de Bruijn Grids and Tilings mathpages.com.
• David Eppstein: Penrose Tiles The Geometry Junkyard. www.ics.uci.edu/~eppstein. Viitattu 28.11.2009. This has a list of additional resources.
• William Chow: Penrose tile in architecture eschertile.com.