Differenssimenetelmä

Differenssimenetelmät ovat matematiikassa käytettyjä menetelmiä, joilla haetaan likimääräistä ratkaisua differentiaaliyhtälöille käyttäen derivaattaa approksimoivia differenssiyhtälöitä.

Intuitiivinen lähestyminen

Differenssimenetelmillä saadaan likimääräinen ratkaisu differentiaaliyhtälöille korvaamalla derivaatan lausekkeet likimäärin vastaavilla erotusosamäärän lausekkeilla. Määritelmän mukaan funktion ensimmäinen derivaatta on

$f'(a)=\lim _{h\to 0}{f(a+h)-f(a) \over h},$

Luonnollinen valinta derivaatan likimääräiseksi laskemiseksi on siten

$f'(a)\approx {f(a+h)-f(a) \over h}$

käyttäen jotakin pientä arvoa h:lle. Tätä lauseketta kutsutaan ensimmäisen derivaatan eteneväksi differenssiapproksimaatioksi. Korvaamalla derivaatan lausekkeet differentiaaliyhtälöissä edellisen kaltaisilla kaavoilla voidaan differentiaaliyhtälöille löytää likimääräiset ratkaisut ilman differentiaali- ja integraalilaskentaa.

Differenssiyhtälöiden johtaminen Taylorin polynomin avulla

Mikäli funktio jonka derivaattaa ollaan approksimoimassa on hyvin käyttäytyvä, niin Taylorin lauseen mukaan

$f(a+h)=f(a)+{\frac {f'(a)}{1!}}h+{\frac {f^{(2)}(a)}{2!}}h^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}h^{n}+R_{n}(a+h),$

missä n! on n:n kertoma ja R_n(a + h) on jäännöstermi, jolla merkitään n:nnen asteen Taylorin polynomin ja alkuperäisen funktion erotusta. Edelleen, jos käytetään esimerkkinä funktion f ensimmäistä derivaattaa, niin Taylorin lauseen mukaan

$f(a+h)=f(a)+f'(a)h+R_{1}(a+h),$

joka voidaan saattaa muotoon

$f'(a)={f(a+h)-f(a) \over h}+{R_{1}(a+h)/h}$

niin, että $R_{1}(a+h)/h$:n ollessa riittävän pieni

$f'(a)\approx {f(a+h)-f(a) \over h}.$

Menetelmän tarkkuus ja kertaluku

Menetelmän virhe määritellään likiratkaisun ja tarkan analyyttisen ratkaisun erotukseksi. Virhelähteitä on kaksi: pyöristysvirhe, joka syntyy tietokoneen pyöristäessä desimaalilukuja sekä diskretointivirhe, joka johtuu siitä, että differenssiyhtälön ratkaisu eroaa tarkasta ratkaisusta, vaikka laskutoimitukset suoritettaisiin täydellisen tarkasti ilman pyöristyksiä.

Differenssimenetelmä perustuu funktion diskretointiin määrätyn hilan mukaisesti.

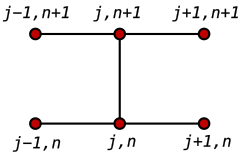
Ensimmäinen asia käytettäessä differenssimenetelmää ongelman ratkaisemiseksi on ongelman määrittelyalueen diskretointi. Useimmiten määrittelyalue jaetaan tasaväliseksi hilaksi (katso yllä oleva kuva). Tämä tarkoittaa sitä, että differenssimenetelmä tuottaa joukon diskreettejä numeerisia ratkaisuja derivaatalle. Useimmiten ratkaisussa on käytetty aika-askelta.

Menetelmän aiheuttamalle paikalliselle diskretointivirheelle voidaan johtaa yleinen lauseke. Paikallista diskretointivirhettä merkitään tyypillisesti isolla o-kirjaimella ja sillä tarkoitetaan virhettä, kun menetelmää on sovellettu yhden kerran. Se on siis erotus $f'(x_{i})-f'_{i}$, kun $f'(x_{i})$ viittaa tarkkaan arvoon ja $f'_{i}$ numeerisesti laskettuun likiarvoon. Taylorin polynomin jäännöstermi on käytännöllinen tutkittaessa diskretointivirhettä. Diskretointivirheen määräävin termi voidaan löytää käyttämällä Lagrangen muotoa Taylorin polynomin jäännöstermille, joka on

$R_{n}(x_{0}+h)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(h)^{n+1}$, missä $x_{0}<\xi <x_{0}+h$,

Jos käytetään taas etenevää differenssiapproksimaatiota ensimmäiselle derivaatalle ja tiedetään, että $f(x_{1})=f(x_{0}+h)$, niin

$f(x_{0}+h)=f(x_{0})+f'(x_{0})h+{\frac {f''(\xi )}{2!}}h^{2},$

josta saadaan edelleen

${\frac {f(x_{0}+h)-f(x_{0})}{h}}=f'(x_{0})+{\frac {f''(\xi )}{2!}}h,$

ja kun edelleen huomataan, että yhtälön vasen puoli on differenssimenetelmän approksimaatio ja oikea puoli on tarkka arvo lisättynä jäännöstermillä, niin nähdään selvästi, että jäännöstermi on paikallinen diskretointivirhe.

Lopulta saadaan tässä esimerkissä:

${\frac {f(x_{0}+h)-f(x_{0})}{h}}=f'(x_{0})+O(h).$

Saatu lauseke ymmärretään niin, että paikallinen diskretointivirhe on verrannollinen askeleen kokoon.

Esimerkki: Ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö

Tarkastellaan esimerkkinä ensimmäisen kertaluvun lineaarista differentiaaliyhtälöä

$u'(x)=3u(x)+2.\,$

Ratkaistaessa tätä yhtälöä Eulerin menetelmällä, käytetään hyväksi erotusosamäärän lauseketta

${\frac {u(x+h)-u(x)}{h}}\approx u'(x)$

jolla saadaan likimääräinen esitys differentiaaliyhtälölle sijoittamalla ensin yllä oleva u'(x):n lauseke differentiaaliyhtälöön ja muokkaamalla tulosta hiukan algebrallisesti, jolloin saadaan

$u(x+h)=u(x)+h(3u(x)+2).\,$

Viimeisin yhtälö on differenssiyhtälö, jonka ratkaisu antaa likimääräisen ratkaisun differentiaaliyhtälölle.

Esimerkki: Lämmönjohtumisyhtälö

Tarkastellaan yksiulotteista lämmönjohtumisyhtälöä homogeenisilla Dirichletin reunaehdoilla

$U_{t}=U_{xx}\,$

$U(0,t)=U(1,t)=0\,$ (reunaehto)

$U(x,0)=U_{0}(x)\,$ (alkuehto)

Yksi tapa ratkaista tämä yhtälö numeerisesti on approksimoida derivaattoja differenssilausekkeilla. Jaetaan määrittelyalue paikan suhteen käyttäen hilapisteitä $x_{0},...,x_{J}$ ja ajassa käyttäen hilapisteitä

$t_{0},....,t_{N}$. Oletetaan, että jako on tasavälinen sekä paikassa että ajassa niin, että jakoväli paikan suhteen on h ja ajan suhteen k. Pisteet

$u(x_{j},t_{n})=u_{j}^{n}$

esittävät likimääräistä numeerista ratkaisua $u(x_{j},t_{n}).$:lle.

Eksplisiittinen menetelmä

Kuvaesitys eksplisiittisen menetelmän differenssille.

Käyttämällä etenevää differenssiapproksimaatiota ajan hetkellä $t_{n}$ ja toisen kertaluvun keskeisdifferenssiä paikassa $x_{j}$, saadaan yhtälö

${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}.\,$

Tämä on eksplisiittinen menetelmä yksiulotteisen lämmönjohtumisyhtälön ratkaisemiseksi.

$u_{j}^{n+1}$:n arvot saadaan muista arvoista seuraavasti:

$u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}$

missä $r=k/h^{2}.$

Jos siis tunnetaan arvot ajan hetkellä n, voidaan vastaavat arvot hetkellä n+1 laskea käyttäen yllä olevaa yhtälöä. Arvot kohdissa $u_{0}^{n}$ ja $u_{J}^{n}$ täytyy korvata reunaehdoilla, jotka tässä esimerkissä ovat molemmat nollia.

Tämä eksplisiittinen menetelmä on numeerisesti vakaa ja konvergoi, kun $r\leq 1/2$. Virhe on verrannollinen aika-askeleeseen ja paikka-askeleen neliöön:

$\Delta u=O(k)+O(h^{2})\,$

Implisiittinen menetelmä

Kuvaesitys implisiittisen menetelmän differenssille.

Kun käytetään takenevaa differenssiapproksimaatiota ajanhetkellä $t_{i+1}$ ja toisen kertaluvun keskeisdifferenssiä paikkaderivaatalle kohdassa $x_{j}$, niin saadaan yhtälö

${\frac {u_{j}^{i+1}-u_{j}^{i}}{k}}={\frac {u_{j+1}^{i+1}-2u_{j}^{i+1}+u_{j-1}^{i+1}}{h^{2}}}.\,$

Tämä on implisiittinen menetelmä yksiulotteisen lämmönjohtumisyhtälön ratkaisemiseksi.

Termit $u_{j}^{i+1}$ saadaan ratkaisemalla lineaarinen yhtälöryhmä:

$(1+2r)u_{j}^{i+1}-ru_{j-1}^{i+1}-ru_{j+1}^{i+1}=u_{j}^{i}$

Tämä menetelmä on aina numeerisesti stabiili ja konvergoi, mutta menetelmä on yleensä laskennallisesti raskaampi kuin eksplisiittinen menetelmä, koska jokaisella aika-askeleella on ratkaistava yhtälöryhmä. Virheet ovat verrannollisia aika-askeleeseen ja paikka-askeleen neliöön.

Crank-Nicolsonin menetelmä

Jos käytetään keskeisdifferenssiä ajanhetkellä $t_{n+1/2}$ ja toisen kertaluvun keskeisdifferenssiä paikkaderivaatalle kohdassa $x_{j}$, niin saadaan yhtälö:

${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {1}{2}}\left({\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}\right).\,$

Tämä kaava tunnetaan Crank-Nicolson menetelmänä.

Crank-Nicolson menetelmän kuvaesitys.

Arvot $u_{j}^{n+1}$ saadaan ratkaisemalla lineaarinen yhtälöryhmä:

$(2+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=(2-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}.\,$

Tämäkin menettely on aina numeerisesti stabiili ja konvergoi, mutta menettely on yleensä laskennallisesti raskaampi kuin eksplisiittinen menetelmä, koska jokaisella aika-askeleella on ratkaistava yhtälöryhmä. Virheet ovat verrannollisia aika-askeleen neliöön ja paikka-askeleen neljänteen potenssiin:

$\Delta u=O(k^{2})+O(h^{4}).\,$

Reunoilla virhe on kuitenkin usein O(h²) eikä O(h⁴).

Yleensä Crank-Nicolson menetelmä on tarkin pienillä aika-askelilla. Eksplisiittinen menetelmä on epätarkin ja se voi olla epävakaa, mutta se on myös helpoin toteuttaa ja on laskennallisesti kevyin. Implisiittinen menetelmä toimii menetelmistä parhaiten, kun aika-askel on suuri.

Lähteet

• Englanninkielinen Wikipedian sivu "Finite Difference Method".
• Mäkinen R., Numeeriset menetelmät, syksy 2007. Luentomoniste.
• Haataja Juha ym., Numeeriset menetelmät käytännössä, CSC - Tieteellinen laskenta Oy 2002.