Soluautomaatti

| Tämän artikkelin tai sen osan kieliasua on pyydetty parannettavaksi. Voit auttaa Wikipediaa parantamalla artikkelin kieliasua. |
Soluautomaatti on tietojenkäsittelytieteessä tutkittu malli, joka käyttää tietokoneohjelmaa "solujen" (engl. cell) vuorovaikutusten simulointiin. Soluautomaatti toteutetaan yleensä kaksiulotteiselle tasolle, jossa se esitetään ruudukkona. Solut voivat olla eri tiloissa, joita voidaan kuvata esimerkiksi värieroilla tai numeroilla. Yleisimmät käytetyt solun tilat ovat "elävä" ja "kuollut". Solun tiloja voi olla suurempikin määrä. Solun tilojen vaihdokset riippuvat solun aikaisemmasta tilasta ja naapurisolujen tilasta.
Monesti muutaman solun tilan ja muutaman vuorovaikutuksen pohjalta syntyy soluautomaattimaailmaa kuvaaviin ruudukoihin tai avaruuksiin hyvinkin mutkikkaita kuvioita, joilla on joskus joitakin elävälle solulle ominaisia piirteitä, kuvio saattaa esimerkiksi jakautua kahtia.
Tunnettu esimerkki soluautomaateista on John Horton Conwayn Game of Life -peli vuodelta 1970[1]. Pelin perusajatus on se, että yksinkertaisten naapurisolujen välisten vuorovaikutusten pohjalta syntyy melko monimutkaisia, muuttuvia kuvioita. Kuvioista käytetään eri nimityksiä, kuten esimerkiksi "Kulkuritykki" tai "Avaruuslaiva". Pelistä on kehitelty lukuisia versioita.
Myöhemmin soluautomaatteja on tehnyt tunnetuksi Stephen Wolfram muun muassa kirjassaan A New Kind of Science (2002).
Jotkut soluautomaatit muistuttavat eläviä soluja, koska niissä on geeni ja ne jakautuvat. Näitä ovat Langtonin silmukat ja niistä johdetut evoloopit.
Soluautomaatin toimintaperiaate
[muokkaa | muokkaa wikitekstiä]
Soluautomaatin ajatus on se, että se koostuu monista soluista, jotka vaihtavat tilaansa valittujen sääntöjen mukaan. Solut on pistetty useimmiten säännöllisen muotoiseen hilaan, joka on monesti 2-ulotteinen suorakulmainen ruudukko. Usein solun tilanvaihdos riippuu naapureista, mutta se voi riippua myös solun menneisyydestäkin. Soluautomaateissa syntyy kohtalaisen mutkikkaita, usein liikkuvia, muuttuvia ja itseään toistavia kuvioita.
Conwayn Life-peli eli "elämän peli" muistuttaa esimerkiksi itseään pelaavaa jätkänshakkia. Peli on nollan pelaajan peli, jota tavallisimmin tietokone pelaa itsekseen. Life-pelin pohjana on tavallisesti suorakulmainen ruudukko, hila, jonka ruudut ovat soluja, jotka voivat olla joko eläviä tai kuolleita.
Elävää solua merkitään usein mustalla, kuollutta valkealla. Värit valitaan usein siten, että näytön tai tietokonetulosteen normaalia taustaväriä lähellä oleva väri merkitsee kuollutta solua.
Soluautomaattia jäljittelevälle systeemille voidaan syöttää alussa vaikkapa satunnaista kohinaa, jossa kuolleita ja eläviä soluja on vieri vieressä satunnaisesti arvottuna. Silloin lähtökohta on mustavalkea sekamelska.
Life-pelissä oleva solu muuttuu ajan mukana seuraavasti:
- Elävä solu, jolla on alle 2 elävää naapuria, kuolee yksinäisyyteen
- Elävä solu, jolla on yli 3 naapuria, kuolee liikakansoitukseen
- Elävä solu, jolla on 2-3 naapuria, säilyy hengissä
- Kuollut solu, jolla on tarkoin kolme elävää solua, alkaa elää.
Tällöin sanotaan, että Conwayn Lifellä on 23/3 sääntö. 23 tarkoittaa, että 2 tai 3 naapurisolua pitävät solun hengissä, ja 3 sitä, että 3 naapurisolua synnyttää uuden solun. Kun tietokone pelaa Life-peliä, mustavalkea sekamelska häviää, ja näytölle ilmestyy monenlaisia ja monenkokoisia ruuduista koostuvia, ajan mukana muuttuvia kuvioita. Life-pelin tyyppisiä soluautomaatteja on laadittu monia. Melko monimutkainen 012345678/3-sääntö tuottaa tikapuumaisia, virtapiiriä muistuttavia kuvioita.
Kehitys yksinkertaisen soluautomaatin sisällä
[muokkaa | muokkaa wikitekstiä]Soluautomaattien on joskus katsottu kuvastavan mutkikkaitten elämän tyyppisten rakenteiden syntymistä yksinkertaisten vuorovaikutusten pohjalta, vaikka luonnon elävät eliöt ovatkin yksinkertaisia soluautomaatteja huomattavasti mutkikkaampia. Stephen Wolframin vuonna 1984 tekemän tutkimuksen Universality and Complexity in Cellular Automata (suomeksi suunnilleen "soluautomaatteissa oleva toistuvuus ja monimutkaisuus") [2] mukaan soluautomaatti voi kehittyä tilanteesta riippuen monella eri tavalla. Soluautomaateilla tuotetut kuviot muistuttavat monesti kaaosteorian mukaisia kuvia.
Soluautomaatti voi tuottaa syöttöarvoista riippuen[3]
- Jatkuvan tilan
- Jaksollisesti vaihtuvia tiloja/säännöllisen kuvion
- Kaoottisen kuvion
- Mutkikkaita, paikallisia, ajan mukana muuttuvia kuvioita, jotka ovat joskus pitkäikäisiä, ja jotka näyttävät sivulta katsoen esimerkiksi haarautuvalta puulta.
Yleensä soluautomaattilaskelmissa annetaan alkuarvoksi satunnainen soluryhmä, jossa on eläviä ja kuolleita soluja sikin sokin. Jatkuvan tilan synnyttäneessä tapauksessa alussa voi esiintyä "eläviä soluja", mutta ne kuolevat muutamassa sukupolvessa pois. Toisessa tapauksessa alun kaoottinen soluryhmä muuttuu säännöllisiksi mustien ja valkoisten solujen kuvioksi. Kolmennessa tapauksessa kaaos säilyy, vaikka yksittäisten solujen tilat muuttuvatkin. Kolmannessa tapauksessa syntyy ajan mukana muotoaan muuttavia soluryhmiä, jotka "elävät" jonkun aikaa, mutta häviävät.
Soluautomaatin tarkka määritelmä
[muokkaa | muokkaa wikitekstiä]
Tarkoin tieteellisesti kuvattuna soluautomaatti on laskettavuusteoriassa, matematiikassa ja teoreettisessa biologiassa tutkittu diskreetti malli. Se on ääretön ja säännöllinen soluista koostuva verkko, jossa jokainen solu on missä tahansa äärellisestä määrästä mahdollisia tiloja. Verkko voi olla n-ulotteinen, kun n on äärellinen kokonaisluku. Soluautomaatin aika kuluu diskreeteissä (ei-jatkuvissa) askelissa, ja solun tila aikana t määräytyy jonkin äärellisen solujoukon (sen ”naapurisolujen”) edellisen aika-askeleen (t-1) tilan funktiona. Solun naapurit pysyvät samoina koko ajan. Jokaisen solun tila muuttuu synkronisesti ja saman muutossäännön mukaan. Joka kerran kun verkon kaikki solut (muutossäännön mukaisesti) muuttuvat syntyy uusi sukupolvi.
Conwayn Lifeä muistuttavia soluautomaatteja
[muokkaa | muokkaa wikitekstiä]-
Diamoeba 5678/35678
-
Räjähtävä kaaos "siemenet" soluautomaatissa, jossa on /2-sääntö eli M:/2. 2 naapuria synnyttää silloin yhden solun. Solun hengissä pysymiselle ei ole tässä automaatissa rajoituksia.

Sääntö 5/345 "Long life", "pitkä elämä", tuottaa hyvin pitkäjaksoisesti muuttuvia kuvioita. Coral 45678/3 tuottaa korallimaisia kuvioita. 1358/357 on hyvin tasapainossa elämän ja kuoleman välillä. 2345/45678 tuottaa kuin linnoitettuja kaupunkeja. "Day & Night" 34678/3678 tuottaa peilikuvasymmetrisiä, melko suuria kuvioita.
Eräs tunnettu Conwayn Life-pelin muunnelma on Nathan Thompsonin kehittämä HighLife-sääntö 23/36. Siinä uusi solu syntyy, jos sillä on 3 tai 6 naapuria, ja elävä solu säilyy seuraavaan sukupolveen, jos sillä on 2 tai 3 naapuria. Eräs säännön tuottamista kuvioista on vinon kuusikulmion muotoinen 12 solusta koostuva "Kopioituja" (Replicator), joka jäljentää itsensä niin kuin elävä solu. Varsinaisessa Life-pelissä ei ole koskaan onnistuttu tuottamaan replikaattoria.
"3D Life":ä pelataan kolmessa ulottuvuudessa, ja solut ovat silloin kuutiomaisia.
Jakautuvia soluja muistuttavia automaatteja
[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Langtonin silmukka
On kokeiltu mutkikkaampia soluautomaatteja, jotka tuovat enemmän esille keinoelämän piirteitä. Silti nämäkin automaatit ovat hyvin yksinkertaisia, eivätkä näin ollen täysin jäljittele luonnossa olevaa elämää. Lisäksi Langtonin silmukat eivät synny tyhjästä, vaan monistuvat vasta sitten, kun mallikappale, hieman 9:ää muistuttava geenijärjestykseltään tietynlainen silmukka on luotu. Myöskään Langtonin silmukka ei tuota elämän tavoin osiaan itse mutkikkaiden geneettisten säätelymekanismien avulla. Langtonin silmukoita on silti onnistuttu tuottamaan hieman alkeellisemmista silmukoista, jotka törmäilevät toisiinsa.
Amerikkalainen biologi Christopher Langton on kehittänyt Langtonin silmukoiksi kutsuttuja soluautomaatteja, joissa on pieni määrä geneettistä informaatiota muistuttavaa koodia.
Langtonin työ perustui alun perin John von Neumann ja Edgar F. Coddin esittämien ajatusten yksinkertaistamisiin.
Langtonin silmukassa on silmukan muotoinen geeni ikään kuin suojakuoren ympäröimänä. Kun aika kuluu, Langtonin silmukka tuottaa itsestään automaattisesti, ilman ohjausta kopioita jakautumalla. Tämä muistuttaa elävien solujen jakautumista. Syntyy korallimainen eliöyhteisö, jossa elävät, jakautuvat eliöt ympäröivät kuolleita eliöitä, samaan tapaan kuin koralliyhdyskunnassa. Silti Langtonin silmukka on eläviä olioita yksinkertaisempi. Langtonin silmukoista on kehitetty eteenpäin kehittyneempiä, paremmin kuvaavia versioita, joita muun muassa japanilaiset tutkivat ahkerasti.
Langtonin silmukan muunnelma "evoloop" kykenee vuorovaikuttamaan ympäristön kanssa ja kehittymään evoluution kautta. Monesti evoloopeja ajava kone luo tilanteen, jossa kilpaillaan elintilasta, ja useimmiten pienimmät evoloopit menestyvät parhaiten, koska kuluttavat vähiten ympäristöä. Joskus evoloopit törmäävät toisiinsa, ja tapahtuu geenien vaihtoa niin kuin bakteerien konjugaatiossa.
SDSR (engl. Structurally Dissolvable Self-Reproducing) eli rakenteisesti hajautuva itsejäljentävä soluautomaattisilmukka kuolee eli hajoaa joissain tilanteissa, mikä vastaa enemmän luonnollista tilannetta.
SDSR Evoloop muistuttaa vielä enemmän luonnollista ekosysteemiä, koska sen eliöt voivat kuolla, vuorovaikuttaa ympäristönsä kanssa ja kehittyä evoluution kautta. Tällä systeemillä on onnistuttu tuottamaan alkeellisemmista silmukoista varsinaisia Langtonin silmukoita.
Langtonin soluautomaateista tunnetaan myös Langtonin muurahaiset, jotka muistuttavat hieman Life-pelin olioita.
Johtomaailma
[muokkaa | muokkaa wikitekstiä]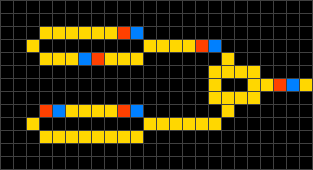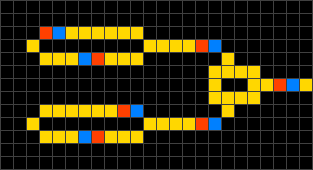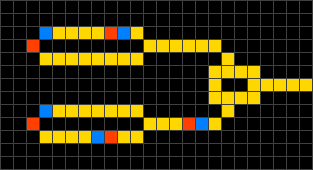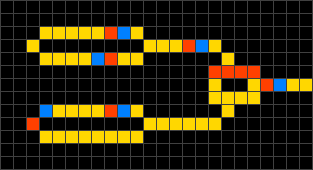
Johtomaailma, englanniksi Wireworld on soluautomaattijärjestelmä, jossa voidaan jäljitellä joitain elektronisia piirejä. Siinä on neljä tilaa, tyhjä, johde, elektronin pää ja elektronin häntä. Nämä muuttuvat toisikseen muutaman säännön mukaisesti.
Syklinen soluautomaatti
[muokkaa | muokkaa wikitekstiä]
David Griffeathin syklisessä soluautomaatissa kohdesolun arvo pysyy vakiona, kunnes naapurisolun arvo kasvaa yhden askeleen suuremmaksi. Tällöin naapurisolun arvo kopioituu kohdesoluun.
Patersonin madot
[muokkaa | muokkaa wikitekstiä]Patersonin madot ovat keinotekoisia yksinkertaisia soluautomaatteja, jotka elävät kuusikulmion muotoisessa hilassa. Madot tuottavat erilaisia kuvioita sen mukaan, minkä säännön mukaan elävät. Osa matojen elinsäännöistä on mahdottomia, ja tappaa madot. Säännöt kuvataan numeroilla niin, että 0 on suoraan eteenpäin, 1 1 askel 60 astetta oikealle, 2 120 astetta oikealla ja niin edelleen.
Toisen asteen soluautomaatti
[muokkaa | muokkaa wikitekstiä]
Toisen asteen soluautomaatti muistaa oman tilansa vielä kahden sukupolven kuluttua. Jos nykyhetki on t, edellinen sukupolvi oli t-1 ja sitä edellinen t-2. Seuraavaa automaatin tilaa luotaessa otetaan huomioon myös edeltävien sukupolvien tila
Näin voidaan johtaa vaikka kuinka monennen asteen soluautomaattaja.
Soluautomaattia muistuttavia järjestelmiä
[muokkaa | muokkaa wikitekstiä]Soluautomaattia muistuttavat hyvin paljon niitä vähemmän tutkitut verkostoautomaatit (network automaton) ja sumeat automaatit.
Katso myös
[muokkaa | muokkaa wikitekstiä]Lähteet
[muokkaa | muokkaa wikitekstiä]- ↑ Claus Emmeche, Tekoelämä, Art House, isbn 951-884-162-4, 1994, sivu 92
- ↑ http://www.stephenwolfram.com/publications/articles/ca/84-universality/4/text.html (Arkistoitu – Internet Archive)
- ↑ Claus Emmeche, Tekoelämä, ISBN 951-884-162-4, Neljäs luku: keinotekoinen kasvu ja evoluutio, Aliluku hahmokoneet ja mallit, sivu 89, Kuva 4.5 ja sivu 92
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä]- Berto, Francesco & Tagliabue, Jacopo: Cellular Automata The Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab. Stanford University. (englanniksi)
- Varje, Jari: Life-peli. Seepia 5 (2002), s. 28-29.
- Ohjelmointiputka Koodivinkit: QBasic: Pelit: Life-peli *QB*
- Soluautomaattien visualisointi Fortran 95:llä
- Game of Life Esimerkkejä ja java-sovelma