Poissonin suhde
Poissonin suhde[1], Poissonin vakio[2] eli Poissonin luku[3] () on materiaalin ominaisuuksia kuvaava suure, joka kuvaa sitä, minkä verran materiaalista tehty kappale sitä puristettaessa levenee tai venytettäessä kapenee poikittaisessa suunnassa. Poissonin suhde on kappaleen poikittaisen ja pitkittäisen venymän suhteen vastaluku.
Poissonin suhde on saanut nimensä ranskalaisen matemaatikko ja fyysikko Siméon Denis Poissonin mukaan. Koska se on eri suunnissa tapahtuvien venymien suhde, se on dimensioton suure.
Merkitys
[muokkaa | muokkaa wikitekstiä]Kun kappaletta, esimerkiksi sauvaa venytetään, se samalla yleensä ohenee poikittaisessa suunnassa. Erityisen helposti tämä on havaittavissa kuminauhasta sen suuren venyvyyden vuoksi. Vastaavasti jos kappaletta puristetaan kokoon, se yleensä laajenee poikittaisessa suunnassa. Tämä sanotaan Poissonin ilmiöksi, ja Poissonin suhde on materiaalin tätä ominaisuutta kuvaava suure.
Kokeellisesti voidaan osoittaa, että kun kappaleen venymä tai puristuma on tarpeeksi pieni, sen poikittaisessa ja pitkittäisessä suunnassa tapahtuvan läpimitan muutos pysyy likipitäen vakiona. Koska kappale yleensä ohenee sitä venytettäessä ja paksunee puristettaessa, tämä suhde on yleensä negatiivinen. Sen vastalukua, joka on yleensä positiivinen, sanotaan materiaalin Poissonin suhteeksi.[4]
Jokaisen vakaan isotrooppisen, lineaariseti kimmoisen materiaalin Poissonin suhde on arvojen -1,0 ja +0,5 välillä, koska tämä suhde sitoo yhteen Youngin moduulin, liukukertoimen ja puristuskertoimen, jotka kaikki ovat aina positiivisia.[5] Useimpien aineiden Poissonin vakio on 0:n ja 0,5:n välillä. Jos se on tasan 0,5, aine on kokoonpuristumatonta eli sen tilavuus ei muutu puristettaessa. Tällaisia aineita ovat esimerkiksi kumi ja parafiini.[4]
Useimmilla teräksillä ja jäykillä polymeereillä luku on lähellä arvoa 0,3, kuitenkin edellyttäen että myötörajaa ei ole ylitetty. Myötörajan yläpuolella, missä muodonmuutokset ovat palautumattomia, Poissonin suhde sen sijaan lähestyy arvoa 0,5.[6] Kumin Poissonin luku on lähellä arvoa 0,5. Korkilla luku on lähellä nollaa, mikä merkitsee, ettei se puristettaessa juuri laajene poikittaisessa suunnassa.
Joissakin harvoissa tapauksissa materiaali päin vastoin kutistuu kokoon myös poikittaisessa suunnassa sitä puristettaessa taikka laajenee myös poikittaisessa suunnassa sitä venytettäessä. Tällaisissa tapauksissa Poissonin suhde on arvoltaan negatiivinen.[7] Sellaisia materiaaleja ovat esimerkiksi jotkut vaahtomuovi, origamiset kalvot[8][9] ja eräät grafiitin muodot.[7]
Anisotrooppisilla materiaaleilla Poissonin suhde ei ole kaikissa suunnissa yhtä suuri ja esimerkiksi hiilinanoputkilla, laskostetuilla lehtimäisillä materiaaleilla[10][11] ja hunajakennojen aukseettisilla metamateriaaleilla[12] se saattaa joissakin suunnissa jopa ylittää arvon 0,5.
Jos oletetaan, että materiaalia venytetään tai puristetaan aksiaalisessa suunnassa eli alla olevan kaavion x-akselin suunnassa, saadaan:
missä
- on Poissonin suhde,
- on poikittainen venymä (kappaletta aksiaalisesti venytettäessä negatiivinen, puristettaessa positiivinen) ja
- on aksiaalinen venymä (positiivinen venytettäessä, negatiivinen puristettaessa).
Pituuden muutos
[muokkaa | muokkaa wikitekstiä]
Oletetaan, että kuutiota venytetään x-suunnassa, kuten oheisessa kuvassa. Sen pituuden muutokselle x-suunnassa käytetään merkintää , kun taas kutistumille y- ja x-suunnissa käytetään merkintää . Tällöin infinitesimaaliset kulmittaiset jännitykset ovat
Jos Poissonin suhe pysyy muodonmuutoksen aikana vakiona, integroimalla nämä lausekkeet saadaan Poissonin suhteenn määritelmän mukaan:
Kun nämä ratkaistaan ja varustetaan eksponenteilla, pituuden muutosten ja välille saadaan yhteys:
Kun pituuden muutokset ja ovat hyvin pieniä, saadaan ensimmäisenä likiarvona:
Tilavuuden muutos
[muokkaa | muokkaa wikitekstiä]Materiaalin muodonmuutoksesta johtuva kuution tilavuuden muutos ΔV/V voidaan nyt laskea. Koska ja , saadaan:
Pituuden ja paksuuden muutosten and välille edellä johdetun yhteyden perusteella saadaan edelleen:
ja hyvin pienillä :n ja :n arvoilla saadaan ensimmäisenä likiarvona:
- .
Isotrooppisille materiaaleille voidaan käyttää Lamén relaatiota[13]
missä on materiaalin puristuvuusmoduuli ja sen Youngin moduuli.
Kaikilla isotrooppisilla aineilla Poissonin suhde on välillä . Teknisiin tarkoituksiin käytetyillä materiaaleilla se on tyypillisesti välillä .[13]
Paksuus muutos
[muokkaa | muokkaa wikitekstiä]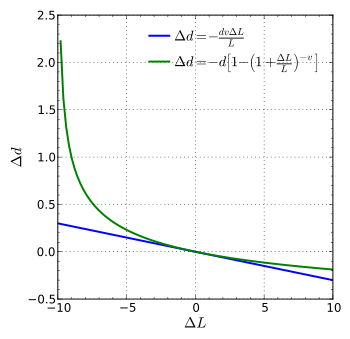
Jos sauvaan, jonka pituus on L ja paksuus d, venytetään sen suuruisella voimalla, että sen pituus kasvaa määrän ΔL, sen paksuuden muutos saadaan lausekkeesta:
Tämä kaava pätee kuitenkin vain, jos muodonmuutokset ovat pieniä. Jos ne ovat suuria, on käytettävä seuraavaa tarkempaa kaavaa:
missä
- on sauvan alkuperäinen paksuus,
- on sen paksuuden muutos,
- on materiaalin Poissonin suhde,
- on sauvan alkuperäinen pituus ennen venytystä ja
- on sen pituuden muutos.
Saatu luku on negatiivinen, mikä osoittaa, että sauvan paksuus pienenee sen pituuden kasvaessa.
Isotrooppiset materiaalit
[muokkaa | muokkaa wikitekstiä]Jos lineaariseen isotrooppiseen materiaaliin kohdistuu vain puristavia (toisin sanoen normaaleja) voimia, kappaleen pituuden muutos yhden akselin suunnassa saa aikaan muodonmuutoksia myös kahden muun ulottuvuuden suuntaisilla akseleilla. Näin ollen on mahdollista yleistää puristavia voimia koskeva Hooken laki kolmeen ulottuvuuteen:
missä:
- , ja ovat venymät -, - ja -akselien suunnissa,
- , ja ovat jännitykset -, - ja -akselien suunnissa,
- on materiaalin Youngin moduuli, joka isotrooppisella materiaalilla on kaikkiin suuntiin sama, ja
- on materiaalin Poissonin suhde, joka niin ikään on isotrooppisella materiaalilla kaikkiin suuntiin sama.
Nämä yhtälöt voidaan yhdistää, jolloin saadaan:
Yleisimmässä tapauksessa normaalien jännitysten lisäksi esiintyy myös leikkausjännityksiä, ja Hooken lain yleistys kokonaisuudessaan voidaan ilmaista yhtälöllä
missä on Kroneckerin delta. Käyttämällä Einsteinin merkintää
yhtälö voidaan kirjoittaa yksinkertaisempaan muotoon:
Anisotrooppiset materiaalit
[muokkaa | muokkaa wikitekstiä]Anistrooppisiksi sanotaan materiaaleja, joiden ominaisuudet eivät ole samat kaikkiin suuntiin. Niillä Poissonin suhde riippuu venytyksen suunnasta. Läpimittojen muutoksia eri suunnssa kuvaavat yhtälöt
Näissä on materiaalin Poissonin suhde, sen Youngin moduuli, venytyksen suuntainen yksikkövektori ja venytykseen nähden kohtisuora yksikkövektori. Anisotropian tyypistä riippuen Poissonin suhde on eri suunnissa eri suuri[14][15].
Ortotrooppiset materiaalit
[muokkaa | muokkaa wikitekstiä]Ortotrooppisille materiaaleille kuten puulle Hooken laki voidaan esittää matriisimuodossa seuraavasti:[16][17]
missä
- on Youngin moduuli akselin suunnassa,
- liukukerroin suunnassa tasolla, joka on kohtisuorassa suuntaan nähden
- on Poissonn suhde, joka vastaa puristumaa suunnassa , kun kappaletta venytetään suunnassa .
Ortotrooppisen materiaalin Poissonin suhde on eri suuri kussakin suunnassa (x, y ja z). Rasitus- ja venytystensorien symmetriasta seuraa kuitenkin, etteivät nämä yhtälössä esiintyvät kuusi suhdetta ole kaikki toisistaan riippumattomia. On vain yhdeksän toisistaan riippumatonta materiaalin ominaisuutta: kolme kimmomoduulia, kolme liukukerrointa ja kolme Poissonin suhdetta. Loput kolme Poissonin suhdetta saadaan yhteyksistä
Näistä yhteyksistä nähdään, että jos on . Poissonin suhteista suurin on tässä tapauksessa ), pienin taas ). Muille Poissonin suhteille voidaan esittää vastaavat yhteydet.
Poikittaisesti isotrooppiset materiaalit
[muokkaa | muokkaa wikitekstiä]Poikittaisesti isotrooppisilla materiaaleilla on isotropiataso, jossa niiden kimmoisuusominaisuudet ovat samat kaikkiin suuntiin. Jos oletetaan että tämä isotropia on -taso, Hooken laki saa muodon[18]
missä isotropiatasoa eli -tasoa on käytetty vakioiden lukumäärän vähentämiseen, sillä .
Jännitys- ja venymätensorien symmetriasta seuraa:
Näin jää jäljelle kuusi toisistaan riippumatonta vakiota: . Poikittaisen isotropian vuoksi on kuitenkin vielä vakioiden ja välillä rajoittava yhteys
Niinpä tällaisten materiaalien kimmoisuusominaisuudet voidaan täysin kuvata viidellä suureella, joista kaksi on Poissonin suhteita. Oletetun symmetriatason suurempi Poissonin suhde on suurempi luvuista ja . Muut suuremmat ja pienemmät Poissonin suhde ovat yhtä suuret.
Eri materiaalien Poissonin suhteita
[muokkaa | muokkaa wikitekstiä]
| Materiaali | Poissonin suhde |
|---|---|
| kumi | 0.4999[20] |
| kulta | 0,42[21] |
| kyllästetty savi | 0,40–0,49 |
| magnesium | 0,29[21] |
| titaani | 0,35[21] |
| kupari | 0,34[21] |
| alumiini | 0,34[21] |
| savi | 0,30–0,45 |
| ruostumaton teräs | 0,30–0,31 |
| teräs | 0,28–0,30[21] |
| valurauta | 0,21–0,30[21] |
| hiekka | 0,20–0,455 |
| betoni | 0,10–0,20 |
| lasi | 0,19–0,35 |
| amorfiset metallit | 0,276–0,409[22] |
| vaahtomuovi | 0,10–0,50 |
| korkki | 0,0 |
| Materiaali | Symmetriataso | ||||||
|---|---|---|---|---|---|---|---|
| hunajakennorakenteinen Nomex | , -akselin suuntainen nauha | 0,49 | 0,69 | 0,01 | 2,75 | 3,88 | 0,01 |
| lasikuitu-epoksihartsi | 0,29 | 0,32 | 0,06 | 0,06 | 0,32 |
Negatiivinen Poissonin suhde ja aukseettiset materiaalit
[muokkaa | muokkaa wikitekstiä]Muutamalla aukseettisiksi kutsutuilla materiaaleilla Poissonin suhde on negatiivinen. Kun niitä venytetään pitkittäisen akselin suunnassa, myös poikittaisessa suunnassa kappaleen läpimitta kasvaa. Tämä aiheutuu yleensä erikoisella tavalla suuntautuneista, saranoituneista molekyylien välisistä sidoksista. Näiden sidosten venyessä pitkittäisessä suunnassa "saranoiden" on ikään kuin auettava poikittaisessa suunanssa, mikä ilmenee poikittaisen läpimitan suurenemisena.[23] Tämä voidaan saada aikaan myös strukturoidusti, mikä on avannut uusia mahdollisuuksia mekaanisten metamateriaalien suunnittelussa .
Tutkimukset ovat osoittaneet, että eräillä puulajeilla ilmenee negatiivinen Poissonin suhde ainoastaan puristuskokeessa, jossa ne saadaan virumaan.[24][25] Aluksi tällaisessa puristuskokeessa Poissonin suhde on positiivinen, mutta se pienenee vähitellen ja saavuttaa lopulta negatiivisen arvon. Näin ollen tämä osoittaa samalla, että puun Poissonin suhde muuttuu ajan myötä, vaikka siihen kohdistuva kuormitus pysyisi vakionakin, mikä osoittaa että sen mittasuhteet pitkittäisessä ja poikittaisessa suunnassa eivät muutu yhtä nopeasti.
Monien aineiden Poissonin suhde voidaan saada negatiiviseksi muuttamalla niiden mikroskooppista rakennetta sopivalla tavalla. Yksinkertaisessa tapauksessa aukseettisuus saadaan aikaan poistamalla osa materiaalista niin, että sen jäljelle jäävä osa muodostaa jaksollisen huokoisen rakennelman.[26]. Hilarakenteisille materiaaleille voidaan saada vielä alempi Poissonin suhde[27], joka isotrooppisessa tapauksessa voi olla mielivaltaisen lähellä arvoa -1[28].
Nykyisin tunnetaan yli 300 kiteistä materiaalia, joilla voidaan saattaa aukseettiseen tilaan suuntaamalla kiteet sopivalla tavalla.[29][30][31]. Sellaisia ovat esimerkiksi Li, Na, K, Cu ,Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb ja MoS.
Poissonin funktio
[muokkaa | muokkaa wikitekstiä]Kun kappaleeseen kohdistuva jännitys on suuri, sen pituuden ja poikittaisen läpimitan ( ja ) välistä yhteyttä ei enää voida tyydyttävästi kuvata vakioksi käsitetyllä Poissonin suhteella. Tällöin Poissonin suhteen sijasta käytetään Poissonin funktiota, jolle on esitetty useita vaihtoehtoisia määritelmiä.[32] Jos poikittaiselle venymälle käytetään määritelmää ja pitkittäiselle ja poikittainen kutistuma on esitettävä pitkittäisen venymän funktiona (toisin sanoen ), yleisimmin käytettyjä ovat Henckyn, Biot'n, Greenin ja Almansin funktiot:
Poissonin ilmiön sovelluksia
[muokkaa | muokkaa wikitekstiä]Poissonin ilmiöllä on suuri vaikutus muun muassa siihen, mitä tapahtuu, kun paineistettu neste tai kaasu virtaa putkessa. Kun paine on suuri, virtaava aine kohdistaa tasaisen voiman putken sisäpintaan ja saa putken laajenemaan leveyssuunnassa. Poissonin ilmiön vuoksi se samalla myös hieman kutistuu pituussuunnassa. Tällä pituuden muutoksella voi olla havaittava vaikutus putkien liitoskohtiin, varsinkin kun sen vaikutukset kertautuvat pitkän putken jokaisessa liitoskohdassa. Jos paine on riittävän suuri, liitokset saattavat irrota, jolloin putkeen syntyy vuoto.
Poissonin ilmiöllä on merkitystä myös rakennegeologiassa. Useimpien muiden materiaalien tavoin kallioperäkin altistuu jännityksen alaisina Poissonin ilmiölle. Geologisessa aikaskaalassa maankuoren jatkuva jatkuva eroosio tai sedimentaatio voi saada aikaan tai poistaa laajoja pystysuuntaisia jännityksiä kallioperän alemmissa kerroksissa. Ne voivat laajeta tai supistus pystysuunnassa niihin kohdistuvan rasituksen vaikutusesta, jolloin niiden muoto samalla muuttuu Poissonin ilmiön vaikutuskesta myös vaakasuorassa suunnassa. Tämän vaakasuoran venymisen tai kutistumisen myötä kallioperään voi syntyä saumakohtia.[33]
Alun perin korkkia alettiin käyttää viinipullojen sulkemiseen sen muiden ominaisuuksien kuten kemiallisen kestävyytensä, läpäisemättömyytensä, taipuisuutensa ja joustavuutensa vuoksi.[34] Myöhemmin se kuitenkin havaittiin sopivan tähän tarkoitukseen erityisen sopivaksi materiaaliksi myös sen vuoksi, koska sen Poissonin suhde on likipitäen nolla. Kun korkki työnnetään pullon suuhun, sen yläosa, joka ei ole vielä sisällä pullossa, ei laajene poikittaisessa suunnassa samalla kun sitä puristetaan pitkittäisessä eli pullon suun suunnassa. Voima, joka tarvitaan korkin työntämiseksi pulloon, kasvaa vain korkin ja pullon välisen kitkan vuoksi. Jos tulppa tehtäisiin esimerkiksi kumista, jonka Poissonin suhde on lähellä arvoa 1/2, tarvittaisiin lisäksi melkoisesti voimaa tulpan paksuuntuneen yläosan puristamiksi niin, että sekin mahtuu pulloon.
Katso myös
[muokkaa | muokkaa wikitekstiä]Lähteet
[muokkaa | muokkaa wikitekstiä]- ↑ Johdatus materiaalien elastisiin ominaisuuksiin Pekka Koskinen, Jyväskylän yliopisto. Viitattu 21.2.2020.
- ↑ Konstitutiiviset yhtälöt, Jännitys- ja muodonmuutostilan yhteys (Sivun 2 alussa) tut.fi. Viitattu 21.2.2020.
- ↑ Taulukko 18: Kimmokerroin, liukukerroin, puristuvuuskerroin ja Poissonin luku genesiskirjat.fi. Arkistoitu 21.2.2020. Viitattu 21.2.2020.
- ↑ a b ”Poissonin luku”, Lujuusoppi, s. 14. Määritä julkaisija! Teoksen verkkoversio. (Arkistoitu – Internet Archive)
- ↑ H. Gercek: Poisson's ratio values for rocks. International Journal of Rock Mechanics and Mining Sciences, 2007, 44. vsk, nro 1, s. 1–13. doi:10.1016/j.ijrmms.2006.04.011
- ↑ Park, RJT. Seismic Performance of Steel-Encased Concrete Piles
- ↑ a b Konstruktiomateriaalit ja niiden valinta: Adaptiiviset materiaalit (Kohta 10.) slideplayer.fi. Viitattu 21.2.2020.
- ↑ Schenk Mark: Folded Shell Structures, PhD Thesis. Cambridgen yliopisto, Claren college, 2011.
- ↑ Z. Y. Wei, Z. G. Guo, L. Dudte, H. Y. Liang, L. Mahadevan: Geometric Mechanics of Periodic Pleated Origami. Physical Review Letters, 2013, 110. vsk, nro 21, s. 215501. PubMed:23745895 doi:10.1103/PhysRevLett.110.215501 Bibcode:2013PhRvL.110u5501W arXiv:1211.6396 Artikkelin verkkoversio.
- ↑ Mayram Eidini, Glaucio H. Paulino: Unraveling metamaterial properties in zigzag-base folded sheets. Science Advances, 2015, 1. vsk, nro 8, s. e1500224. PubMed:26601253 PubMed Central:4643767 doi:10.1126/sciadv.1500224 ISSN 2375-2548 Bibcode:2015SciA....1E0224E arXiv:1502.05977
- ↑ Maryam Eidini: Zigzag-base folded sheet cellular mechanical metamaterials. Extreme Mechanics Letters, 2016, s. 96–102. doi:10.1016/j.eml.2015.12.006 arXiv:1509.08104
- ↑ Davood Mousanezhad, Sahab Babaee, Hamid Ebrahami, Ranajay Ghosh, Abdemagid Salem Hamouda, Katia Bertholdi, Ashkan Vaziri: Hierarchical honeycomb auxetic metamaterials. Scientific Reports, 2015, nro 5. PubMed:26670417 PubMed Central:4680941 doi:10.1038/srep18306 ISSN 2045-2322 Bibcode:2015NatSR...518306M
- ↑ a b Limits to Poisson’s ratio in isotropic materials – general result for arbitrary deformation arxiv.org. Viitattu 21.2.2020.
- ↑ A: I. Epishin, D. S. Lisovenko: Extreme values of Poisson's ratio of cubic crystals. Technical Physics, 2016, 61. vsk, nro 10, s. 1516–1524. doi:10.1016/j.mechmat.2019.03.017 Bibcode:2016JTePh..61.1516E
- ↑ V. A. Gorodtsov, D. S. Lisovenko: Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals. Mechanics of Materials, 2019, nro 134, s. 1–8. doi:10.1016/j.mechmat.2019.03.017
- ↑ A. P. Boresi, R. J. Schmidt, O. M. Sidebottom: Advanced Mechanics of Materials. Wiley, 1993.
- ↑ SG. Lekhnitskii: Theory of elasticity of an anisotropic elastic body. Holden-Day Inc, 1963.
- ↑ S. C. Tan: Stress Concentrations in Laminated Composites. Lancaster, Pennsylvania: Techomic Publishinc Company, 1994.
- ↑ Poisson's Ratio Calculation for Glasses glassproperties.com. Viitattu 21.2.2020.
- ↑ Archived copy polymerphysics.net. Arkistoitu 31.10.2014. Viitattu 24.9.2014.
- ↑ a b c d e f g Esko Valtanen: ”Kimmokerroin, liukukerroin, puristuvuuskerroin ja Poissonin luku”, Matemaattisia kaavoja ja taulukoita, s. 405–406. Genesis-kirjat, 2013. ISBN 978-952-9867-37-0
- ↑ Journal of Applied Physics 110, 053521 (2011)
- ↑ Negative Poisson's ratio silver.neep.wisc.edu. Viitattu 21.2.2020.
- ↑ Tomasz Ozyhar, Stefan Hering, Peter Niemz: Viscoelastic characterization of wood: Time dependence of the orthotropic compliance in tension and compression. Journal of Rheology, 6.2.2013, 57. vsk, nro 2, s. 699–717. doi:10.1122/1.4790170 ISSN 0148-6055 Bibcode:2013JRheo..57..699O
- ↑ Jiali Jiang, Bachtiar Erik Valentine, Lu Jianxiong, Peter Niemz: Time dependence of the orthotropic compression Young's moduli and Poisson's ratios of Chinese fir wood. Holzforschung, 1.11.2016, 70. vsk, nro 11, s. 1093–1101. doi:10.1515/hf-2016-0001 ISSN 1437-434X Artikkelin verkkoversio.
- ↑ Giorgio Carta, Michele Brun, Antonio Baldi: Design of a porous material with isotropic negative Poisson's ratio. Mechanics of Materials, 2016, nro 97, s. 67–75. doi:10.1016/j.mechmat.2016.02.012
- ↑ Luigi Cabras, Michele Brun: A class of auxetic three-dimensional lattices. Journal of the Mechanics and Physics of Solids, 2016, nro 91, s. 56–72. doi:10.1016/j.jmps.2016.02.010 Bibcode:2016JMPSo..91...56C arXiv:1506.04919 Artikkelin verkkoversio.
- ↑ Luigi Cabras, Michele Brun: Auxetic two-dimensional lattices with Poisson's ratio arbitrarily close to -1. Proceedings of the Royal Society A, 2014, 470. vsk, nro 2172, s. 20140538. doi:10.1098/rspa.2014.0538 Bibcode:2014RSPSA.47040538C arXiv:1407.5679
- ↑ Classification of cubic auxetics. Physica Status Solidi B, 2013, 250. vsk, nro 10, s. 2038–2043. doi:10.1002/pssb.201384233 (englanti)
- ↑ R. V. Goldstein, V. A. Gorodtsov, D. S. Lisovenko: Variability of elastic properties of hexagonal auxetics. Doklady Physics, 2011, 56. vsk, nro 112, s. 602–605. doi:10.1134/S1028335811120019
- ↑ R. V. Goldstein, V. A. Gorodtsov, D S. Lisovenko, M. A. Volkov: Auxetics among 6-constant tetragonal crystals. Letters on Materials, 2015, 5. vsk, nro 4, s. 409–413. doi:10.22226/2410-3535-2015-4-409-413 Artikkelin verkkoversio.
- ↑ L. A. Mihai, A. Goriely: How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity. Proceedings of the Royal Society A, 3.11.2017, 47. vsk, nro 2207. PubMed:29225507 PubMed Central:5719638 doi:10.1098/rspa.2017.0607 Bibcode:2017RSPSA.47370607M
- ↑ Structural Geology Lecture 18: Effective Stress .geosc.psu.edu. Viitattu 21.2.2020.
- ↑ S. P. Silva, M. A. Sabino, E. M. Fernandes, V. M. Correlo, L. F. Boesel, R. L. Reis: Cork: properties, capabilities and applications. International Material Reviews, 2005, 50. vsk, nro 6, s. 345–. Artikkelin verkkoversio.


























![{\displaystyle \varepsilon _{xx}={\frac {1}{E}}\left[\sigma _{xx}-\nu \left(\sigma _{yy}+\sigma _{zz}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2a4a45070b5bcb57f202d91db12bd6d3e7904d)
![{\displaystyle \varepsilon _{yy}={\frac {1}{E}}\left[\sigma _{yy}-\nu \left(\sigma _{xx}+\sigma _{zz}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94d85b30fba005ed4c443b6a984061dbe5c2f9a)
![{\displaystyle \varepsilon _{zz}={\frac {1}{E}}\left[\sigma _{zz}-\nu \left(\sigma _{xx}+\sigma _{yy}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07315b9cd2f3dc0b9014aad0b33dbf41fcb5ffa)









![{\displaystyle \varepsilon _{ii}={\frac {1}{E}}\left[\sigma _{ii}(1+\nu )-\nu \sum _{k}\sigma _{kk}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c171da9cc07267bd75872ef5cf780786ec35054)
![{\displaystyle \varepsilon _{ij}={\frac {1}{E}}\left[\sigma _{ij}(1+\nu )-\nu \delta _{ij}\sum _{k}\sigma _{kk}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e72a6a8028c583aa887514378ab4c22a83cd7b47)


![{\displaystyle \varepsilon _{ij}={\frac {1}{E}}\,\left[\sigma _{ij}(1+\nu )-\nu \delta _{ij}\sigma _{kk}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beaf0dc7aecf767b9ca204e8cd98596f7110d5a9)

































![{\displaystyle {\begin{aligned}\nu ^{\text{Hencky}}&=-{\frac {\ln \lambda _{\text{trans}}}{\ln \lambda _{\text{axial}}}}\\[2pt]\nu ^{\text{Biot}}&={\frac {1-\lambda _{\text{trans}}}{\lambda _{\text{axial}}-1}}\\[2pt]\nu ^{\text{Green}}&={\frac {1-\lambda _{\text{trans}}^{2}}{\lambda _{\text{axial}}^{2}-1}}\\[2pt]\nu ^{\text{Almansi}}&={\frac {\lambda _{\text{trans}}^{-2}-1}{1-\lambda _{\text{axial}}^{-2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7e1d737a272ed4551cc65d722901df6ead6badf)
