Napoleonin lause

Napoleonin lause sen alkuperäisessä muodossa.

Napoleonin lause on geometriaan liittyvä tulos, joka todistaa erään kolmioon liittyvän konstruktion synnyttävän sisäänsä aina tasasivuisen kolmion. Konstruktio muodostetaan mielivaltaiseen kolmioon siten, että jokaiselle kolmion sivulle piirretään tasasivuinen kolmio, jonka sivu yhtyy kolmion sivun kanssa ja jonka kolmas kärki osoittaa ulospäin kolmiosta. Näin kolmio on ympäröity kolmella tasasivuisella kolmiolla. Jokaiselle tasasivuiselle kolmiolle merkitään keskustaan, eli painopisteeseen, piste, jotka yhdistetään janoilla kolmioksi. Tämä kolmio on väitteen mukaan tasasivuinen kolmio.

Napoleonin lauseen variaatioita

Napoleonin lauseen alkuperäinen muoto synnyttää aina tasasivuisen kolmion (engl. outer Napoleon's triangle ). Napoleonin lause pätee myös sellaiselle konstruktiolle, jossa tasasivuisten kolmioiden yhdet sivut yhtyvät kolmion sivuihin, mutta kolmioiden kolmas kärki osoittaa kolmioiden sisäpuolellepäin. Tämä Napoleonin kolmio on joskus edellistä pienempi (engl. inner Napoleon triangle ).

Jos yhden tasasivuisen kolmion kärki osoittaa sisäänpäin ja kaksi muuta ulospäin kolmiosta, saadaan kolmioiden keskipisteistä tasakylkinen kolmio, jonka kulmat ovat 30°, 30° ja 120°.

Kolmiota ympäröivien kolmioiden ei tarvitse olla tasasivuisia kolmioita: kolme yhdenmuotoistakin kolmiota riittää. Piirretään ensin alkuperäinen satunnainen kolmio. Valitaan toinen kolmio, sekin satunnainen muodoltaan, ja numeroidaan sen sivut 1, 2 ja 3. Siirretään toisen kolmion sivu 1 alkuperäisen kolmion kylkeen suurentaen kolmiota niin, että sivut yhtyvät samanpituisiksi. Kopioidaan toinen kolmio uudeksi kolmioksi ja siirretään se lähes samassa asennossa ja suurennetaan sitä niin, että sivu 2 yhtyy kolmion toisen sivun kanssa. Sama toistetaan toisen kopion kanssa niin, että lähes samassa asennossa sen kolmas sivu yhtyy jäljellä olevaan vapaaseen sivuun. Nyt alkuperäinen kolmio on ympäröity yhdenmuotoisilla kolmioilla. Valitaan näiden sisältä piste, joka sijaitsee kaikissa kolmessa kolmioissa samassa suhteellisessa kohdassa. Yhdistetään nämä pisteet janoilla ja nyt on syntynyt kolmio, joka on yhdenmuotoinen ympäröivien kolmioiden kanssa.

• 
  Napoleonin lause
• 
  Napoleonin lause, kulma C 120 astetta
• 
  Napoleonin lause, kulma C yli 120 astetta
• 
  Napoleonin lause, tasasivuiset kolmiot sisäänpäin
• 
  Napoleonin lause, tasasivuiset kolmiot sisäänpäin

Merkillisiä pisteitä: Napoleonin pisteet

Konstruktioon liittyy myös eräitä kolmion merkillisiä pisteitä. Merkilliset pisteet syntyvät kolmen janan tai suoran leikkauspistenä, joiden olemassaolo on riippumaton kolmion sivujen pituuksista. Molempiin edellä esitelyihin konstruktioihin liittyvät Napoleonin pisteet, jotka liittyvät kolmen janan yhteisiin leikkauspisteisiin. Kolmion kärjet yhdistetään vastaisen sivun tasasivuisen kolmion keskipisteisiin. Kun tasasivuisten kolmioiden kärjet osoittavat kolmiosta ulospäin, syntyy ensimmäinen Napoleonin piste , kun kärjet osoittavat sisäänpäin, syntyy toinen Napoleonin piste .

Samassa kontruktioissa voidaan yhdistää kolmion kärjet tasasivuisten kolmioiden uloimpiin kärkiin. Nämä janat leikkaavat Fermat'n pisteissä. Kun tasasivuiset kolmioiden kärjet osoittavat ulospäin kolmiosta, saadaan ensimmäinen Fermat'n piste , ja kun kärjet osoittavat kolmiosta sisäänpäin, saadaan toinen Fermat'n piste .

Todistus

Oheisessa todistuksessa tarvittava apupiirros.

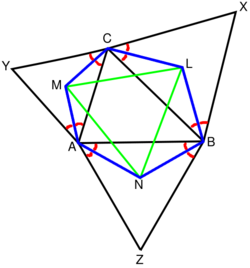
Napoleonin lauseen väite, jossa tasasivuisten ulkokolmioiden keskipisteet yhdistävät janat muodostavat myös tasasivuisen kolmion, voidaan todistaa alla esitetyllä tavalla. Merkitään ensin pisteet L, M ja N tasasivuisten kolmioiden keskipisteisiin. Tasasivuisen kolmion keskipiste sijaitsee kolmion kulmien kulmanpuolittajien leikkauspisteessä.

Aluksi voidaan tehdä kaksi yleistä huomiota. Kolmion sivun ja kulmanpuolittajan väliin jää 30° kulmat:

$\measuredangle MCA=\measuredangle CAM=\measuredangle NAB=\measuredangle ABN=\measuredangle LBC=\measuredangle BCL=30^{\circ }.$

Tasasivuisten kolmioiden yhdenmuotoisuudesta seuraa myös

${\frac {|AM|}{|AC|}}={\frac {|AN|}{|AB|}}={\frac {|CL|}{|BC|}}$.

Nyt kolmiossa $\scriptstyle \triangle AMC$, jakamalla jana AC ensin puoliksi pisteellä C', syntyy kohtaan C' suora kulma janojen AC' ja C'M välille. Sivujen kosini antaa

$\cos 30^{\circ }={\frac {|AC\ '|}{|AM|}}\Leftrightarrow {\frac {\sqrt {3}}{2}}={\frac {{\tfrac {1}{2}}|AC|}{|AM|}}\Leftrightarrow {\frac {\sqrt {3}}{1}}={\frac {|AC|}{|AM|}}\Leftrightarrow {\frac {3}{\sqrt {3}}}={\frac {|AC|}{|AM|}}$,

joten

$|AM|={\tfrac {\sqrt {3}}{3}}|AC|$.

Vastaavasti kolmiossa $\scriptstyle \triangle ANB$ on

$|AN|={\tfrac {\sqrt {3}}{3}}|AB|$.

Kärjen A ympäristössä myös kulmat

$\measuredangle ZAN=\measuredangle MAY=30^{\circ }$

ja, kuten kuviosta voidaan päätellä, myös

$\measuredangle NAM=\measuredangle ZAC$.

Nyt kolmiot ovat yhdenmuotoiset eli $\scriptstyle \triangle AMN\sim \triangle ACZ$ (mittakaavalla $\scriptstyle {\sqrt {3}}\,:\,3)$, koska

• kulma $\measuredangle NAM=\measuredangle ZAC$,
• pituus $|AM|={\tfrac {\sqrt {3}}{3}}|AC|$
• ja pituus $|AN|={\tfrac {\sqrt {3}}{3}}|AB|={\tfrac {\sqrt {3}}{3}}|AZ|$.

Tällöin Napoleonin kolmion sivulle NM saadaan

$|NM|={\tfrac {\sqrt {3}}{3}}|ZC|$.

Vastaavasti voidaan päätellä kärjen B ympäristössä sivulle LN (valitsemalla janat peilikuvamaisesti), että

$|NL|={\tfrac {\sqrt {3}}{3}}|ZC|$,

joten sivut NM ja LN ovat yhtä pitkät

$|NM|=|LN|$.

Siirtämällä vastaava tarkastelu kärkien B ja C ympäristöihin, saadaan vuorostaan

$|LN|={\tfrac {\sqrt {3}}{3}}|AX|$ ja

$|LM|={\tfrac {\sqrt {3}}{3}}|AX|$, joten

$|LM|=|LN|$ ja vielä $=|MN|$. Kolmion kaikki sivut ovat samanmittaisia.

Historia

Lause on legendaarisesti liitetty Napoléon Bonaparteen (1769-1821), mutta nykyään sen todellisesta keksijästä on monia mielipiteitä. Sen vaiheita on pystytty seuraamaan taaksepäin vuoteen 1825, kun William Rutherford sisällytti sen kirjaansa "The Ladies Diary". Lause on todennäköisesti tätä vanhempi.

Napoleon oli kuitenkin matematiikassa huomattavan lahjakas. Hänet aiottiin tämän vuoksi siirtää laivaston palvelukseen, mutta sitten hänen taitojaan katsottiin tarvittavan tykistössä, joka tuohon aikaan kehittyi voimakkaasti. Hän oli myös Institute de France'n jäsen, mistä hän oli ylpeä ja tunsi useita sen ajan tunnettuja matemaatikoita. Hän kävi heidän kanssaan lukuisia geometriaan liittyviä keskusteluita ja ratkoi heidän kanssaan geometrisia probleemoja.

Katso myös

• Fermat'n pisteet

Lähteet

• Wells, David: The Penquin Dictionary of Curious and Interesting Geometry. Englanti: Penguin Group, 1991. ISBN 0-14-011813-6 (englanniksi)

Aiheesta muualla

• PlanetMath: Napoleon’s theorem
• MathPages: Napoleon's Theorem
• Ballew, Pat: Napoleon's Thm and the Napoleon Points (Arkistoitu – Internet Archive)
• Kivelä, Simo K.: Napoleonin lause
• Kivelä, Simo K.: Napoleonin lause todistuksineen kompleksiluvuilla
• Kivelä, Simo K.: Geometriakulma: Napoleonin lause
• Kivelä, Simo K.: Geometriakulma: Algebran käyttö geometriassa eli Napoleonin lause uudelleen
• Matematiikkakilpailut.fi: Nimekästä geometriaa (myös Napoleonin lauseen todistus) (Arkistoitu – Internet Archive), Matematiikan olympialaisten valmennusmateriaalia
• http://www.ms.uky.edu/~droyster/courses/fall11/MA341/Classnotes/Lecture%2017.pdf