Lautapasianssi

Wikipediasta
Siirry navigaatioon Siirry hakuun
Soubisen prinsessa Anne de Rohan-Chabot pelaa lautapasianssia, 1697

Lautapasianssi[1] eli erakkopeli[2] (engl. Solitaire tai Peg Solitaire, ransk. Solitaire) on yhden hengen lautapeli, jossa nappuloita tai kuulia siirretään peli­laudalla ruudusta tai tavallisimmin reiästä toiseen siten, että jokaisella siirrolla jonkin nappula hyppää toisen nappulan yli, joka tällöin poistetaan pelistä.

Varhaisin tieto pelistä on Ranskasta Ludvig XIV:n ajalta, vuodelta 1697, jolloin Claude August Berey teki Soubisen prinsessa Anne de Rohan-Chabot'ta esittävän kaiverruksen, jossa hänellä oli tämä peli kädessään. Saman vuoden elokuussa ranskalaisessa kirjallisessa aikakaus­kirjassa Mercure galant julkaistiin kuvaus tästä pelistä ja sen säännöistä.

Yleensä pelilaudan kaikkiin reikiin yhtä lukuun ottamatta sijoitetaan aluksi nappula.

Pelistä on useita muunnelmia, joista tunnetuimmat ovat englantilainen lauta­pasianssi[1] eli englanti­lainen erakko­peli[2] sekä ranska­lainen lauta­pasianssi[1] eli ranska­lainen erakko­peli[2] Englanti­laisen pelin laudalla on 33 reikää, jotka muodostavat ristimäisen kuvion, ranska­laisen pelin laudalla reikiä on 37.

Englantilaisessa lauta­pasianssissa sijoitetaan yleensä nappula aluksi pelilaudan kaikkiin muihin paitsi keskimmäiseen reikään. Tavoitteena on saada poistetuksi kaikki nappulat yhtä lukuun ottamatta, joka mieluiten jää keskimmäiseen reikään.[2]

Ranskalaisessa lauta­pasianssissa täytetään yleensä alun alkaenkin vain osa rei'istä.[2] Tällaisella laudalla tehtävä ei olisikaan ratkaistavissa, jos vain keskimmäinen reikä jätettäisiin aluksi tyhjäksi.

Pelilauta

[muokkaa | muokkaa wikitekstiä]
Englantilainen lautapasianssi
Ranskalainen lautapasianssi

Englantilaisen ja ranskalaisen pelin laudat reikineen on esitetty oheisissa kaaviossa. Niissä '.' merkitsee reikää, johon aluksi sijoitetaan nappula, 'o' tyhjäksi jätettävää reikää.

Englantilainen Ranskalainen 
     · · ·
     · · ·
 · · · · · · · 
 · · · o · · · 
 · · · · · · · 
     · · ·
     · · ·

     · · ·
   · · · · ·
 · · · · · · · 
 · · · o · · · 
 · · · · · · · 
   · · · · ·
     · · ·

Peli

[muokkaa | muokkaa wikitekstiä]
Lautapasianssia pelaava mies

Jokaisella siirrolla yhtä nappulaa siirretään kohti­suorasti viereisen nappulan yli, kaksi askelta kerrallaan, jolloin välissä oleva nappula samalla poistetaan pelistä.

Seuraavissa kaavioissa · merkitsee reikää, jossa on nappula, * osoittaa nappulan, jota kulloinkin siirretään, ja o merkitsee tyhjää reikää. Sininen ¤ tarkoittaa reikää, josta nappula kulloinkin siirretään, ja punainen o sitä reikää, jossa oleva nappula poistetaan hyppäämällä sen yli.

Täten sallitut siirrot kuhunkin neljään suuntaan ovat: 

* · o  →  ¤ o *  Hyppy oikealle

o · *  →  * o ¤  Hyppy vasemmalle

*     ¤
·  →  o  Hyppy alas
o     *

o     *
·  →  o  Hyppy ylös
*     ¤

Englantilaisella laudalla kolme ensimmäistä siirtoa voivat olla esimerkiksi: 

    · · ·             · · ·             · · ·             · · · 
    · * ·             · ¤ ·             · o ·             · * · 
· · · · · · ·     · · · o · · ·     · ¤ o * · · ·     · o o o · · ·
· · · o · · ·     · · · * · · ·     · · · · · · ·     · · · ¤ · · ·
· · · · · · ·     · · · · · · ·     · · · · · · ·     · · · · · · ·
    · · ·             · · ·             · · ·             · · ·
    · · ·             · · ·             · · ·             · · ·

Strategia

[muokkaa | muokkaa wikitekstiä]

Pelissä tulee helposti tehdyksi virheitä siten, että päädytään tilanteeseen, jossa on kaksi tai kolme kaukana toistaan sijaitsevaa nappulaa. Tällöin peliä ei voida jatkaa loppuun. Monet ratkaisua yrittäneet eivät ole siinä koskaan onnistuneet.

Tehtävä voidaan ratkaista monella eri tavalla. Niiden esittämiseksi reikiä merkitään usein kirjaimilla seuraavasti: 

Englantilainen     Ranskalainen
    a b c             a b c
    d e f           y d e f z
g h i j k l m     g h i j k l m
n o p x P O N     n o p x P O N
M L K J I H G     M L K J I H G
    F E D           Z F E D Y
    C B A             C B A

Tällaista peilikuvamaista merkitä­tapaa käytetään muun muassa siitä syystä, koska ranskalaisella laudalla pelataan usein niin, että tyhjäksi jätetään jokin muu kuin keskimmäinen reikä ja tavoitteena on, että viimeinen nappula jää vastakkaisella puolella vastaavassa kohdassa olevaan reikään. Englanti­laisella laudalla peliä voidaan peltata vaihto­ehtoisesti niinkin, että jokin muu kuin keskimmäinen reikä jätetään tyhjäksi, jolloin tavoitteena on, että viimeinen nappula jää samaan reikään.

Ranskalaisella laudalla peli ei olekaan ratkaistavissa, jos vain keskimmäinen reikä jätetään tyhjäksi ja vain kohti­suorat siirrot sallitaan. Tämän on Hans Zantema todistanut seuraavasti. Jaetaan reiät seuraavalla tavalla kolmeen luokkaan, joille käytetään merkintöjä A, B ja C: 

    A B C
  A B C A B
A B C A B C A
B C A B C A B
C A B C A B C
  B C A B C
    A B C

Kun aluksi vain keskimmäinen reikä on tyhjä, A:lla merkittyjä täytettyjä reikiä on 12, B:llä ja C:llä merkittyjä samoin 12 kumpiakin. Jokaisella siirrolla A:lla merkittyjen, täytettyjen reikien luku­määrä joko kasvaa tai vähenee yhdellä, ja samoin on B:llä ja C:llä merkittyjen reikien laita. Niinpä kun siirtoja on tehty parillinen määrä, kaikki nämä lukumäärät ovat parillisia, ja kun niitä on tehty pariton määrä, kaikki nämä lukumäärät ovat parittomia. Niinpä loppu­tilanteeseen, jossa on vain yksi nappula jäljellä, ei voida päätyä: silloin nimittäin yksi näistä lukumääristä olisi 1, siis pariton luku, molemmat muut lukumäärät nollia, siis parillisia.

Tavallisimmin ranskalaisella laudalla aloitetaankin tilanteesta, jossa tyhjiksi on alku­tilanteessa jätetty ylempänä olevassa kaavioissa kirjaimilla A, B, C, G, M, N, a, b, c, g, m ja n merkityt reiät. Tästä alku­tilanteesta lähtien tehtävä on ratkaistavissa siten, että viimeinen nappula jää reikään x.[2]

Sitä vastoin englantilaisella laudalla tehtävä on ratkaistavissa myös lähtemällä alku­tilanteesta, jossa vain keskimmäinen reikä on tyhjä. Tämä on mahdollista, koska tässä kaaviossa B:llä merkittyjen reikien lukumäärä on 10, A:lla ja C:llä merkittyjen kumpienkin 11.

Muuan sovellettavissa oleva taktiikka on jakaa pelilauta kolmen reiän osiin, poistaa niistä kaikki nappulat käyttämällä yhtä ulkopuolelta tulevaa nappulaa, joka hyppää alueelle ja sitten sieltä takaisin. Alla olevassa esimerkissä * on tämä ulkopuolelta tuleva nappula. 

* · o      ¤ o *      o * ·      * o ¤
  ·     →    ·    →     o     →    o
  ·          ·          ¤          o

Tätä menetelmää voidaan soveltaa kolmen nappulan riviin, 2·3 nappulan täyttämään suorakulmaiseen alueeseen tai kuuteen nappulaan, jotka ovat sijoittuneet L:n muotoon alueeseen, jonka pituus on 4 ja leveys 3 reikää.

Pelistä on myös vaihtoehtoisia muunnelmia, joissa tyhjä reikä jätetään aluksi muualle kuin keskimmäiseen reikään ja tavoitteena on jättää viimeinen nappula johonkin tiettyyn reikään. Englantilaisella laudalla tämä on mahdollista, olipa alkuperäinen reikä missä tahansa, mutta viimeinen nappula voi jäädä ainoastaan reikiin, joiden etäisyys alkuperäisestä tyhjästä reiästä on kolmen monikerta. Täten jos aluksi reikä a on tyhjä, viimeisen nappulan ainoat mahdolliset paikat ovat a, p, O ja C.

Peliä koskevia tutkimuksia

[muokkaa | muokkaa wikitekstiä]

Peliä ovat tutkineet matemaattiselta kannalta muun muassa Elwyn R. Berlekamp, John Horton Conway ja Richard K. Guy.[3] He ottivat käyttöön pagodafunktion käsitteen, jonka avulla voidaan tehokkaasti selvittää, missä tapauksessa tehtävä on ratkaistavissa, missä tapauksessa ei. Annettua asetelmaa vastaavan pagoda­funktion löytäminen voidaan muotoilla lineaariseksi ohjelmointi­tehtäväksi, joka on ratkaistavissa polynomiaalisessa ajassa.

Julkaisematon tutkielma vuodelta 1989 käsittelee yleistettyä versiota pelistä englantilaisella laudalla. Se osoitti, että yleistetyssä pelissä jokaisella ratkaistavissa olevalla tehtävällä on 29 erilaista ratkaisuja, symmetrioita lukuun ottamatta, kun englantilaisella laudalla on kaikkiaan 9 erillistä 3×3 reiän muodostamaa neliötä. Tutkielmassa saatiin myös alaraja sellaisten mahdollisten ratkaistavissa olevien käänteisten asetelmien probleemojen koolle, joissa nappuloiden pitää lopuksi jäädä samoihin reikiin, jotka aluksi ovat tyhjinä. Jokaisen sellaisen tehtävän ratkaisussa on sen tarkemmista yksityis­kohdista riippumatta vähintään 11 siirtoa.

Abstraktin algebran avulla voidaan osoittaa, että jos pelissä jää lopuksi jäljelle vain yksi nappula, pelilaudalla on vain viisi sellaista reikää, joihin se voi jäädä.[4]

Englantilaisen pelin ratkaisu

[muokkaa | muokkaa wikitekstiä]

Englantilaisen pelin lyhyin ratkaisu käsittää 18 siirtoa, mikäli sarjahypyt, jolloin samalla nappulalla tehdään useita hyppyjä peräkkäin, lasketaan yhdeksi siirroksi.

Tämän ratkaisun esitti Ernest Bergholt vuonna 1912, ja vuonna 1964 John Beasley todisti sen lyhimmäksi.

Muut ratkaisut sisältyvät seuraavaan luetteloon. Käytetyt merkinnät ovat:

  • Ennen kaksoispistettä: reikä, joka aluksi on tyhjä
  • kaksoispisteen ja yhtäläisyysmerkin jäljessä: reikä, johon viimeinen nappula jää
  • yhtäläisyysmerkin jälkeen: luettelo siirroista; kukin siirto merkitään kahdella kirjaimella, joista ensimmäinen tarkoittaa nappulan sijaintia ennen siirtoa, jälkimmäinen sen sijaintia siirron jälkeen (jakoviivaa / käytetään pilkun sijasta erottamaan toistaan selvät muutaman siirron sarjat kuten kuuden nappulan muodostaman alueen tyhjentäminen)
x:x=ex,lj,ck,Pf,DP,GI,JH,mG,GI,ik,gi,LJ,JH,Hl,lj,jh,CK,pF,AC,CK,Mg,gi,ac,ck,kI,dp,pF,FD,DP,Pp,ox
x:x=ex,lj,xe/hj,Ki,jh/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/PD,GI,mG,JH,GI,DP/Ox
j:j=lj,Ik,jl/hj,Ki,jh/mk,Gm,Hl,fP,mk,Pf/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/Jj
i:i=ki,Jj,ik/lj,Ik,jl/AI,FD,CA,HJ,AI,JH/mk,Hl,Gm,fP,mk,Pf/ai,ca,fd,hj,ai,jh/gi,Mg,Lh,pd,gi,dp/Ki
e:e=xe/lj,Ik,jl/ck,ac,df,lj,ck,jl/GI,lH,mG,DP,GI,PD/AI,FD,CA,JH,AI,HJ/pF,MK,gM,JL,MK,Fp/hj,ox,xe
d:d=fd,xe,df/lj,ck,ac,Pf,ck,jl/DP,KI,PD/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/MK,gM,hL,pF,MK,Fp/pd
b:b=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp,ox/xe/AI/BJ,JH,Hl,lj,jb
b:x=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp,ox/xe/AI/BJ,JH,Hl,lj,ex
a:a=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/ia
a:p=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/dp


Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen.
Voit auttaa Wikipediaa tekemällä käännöksen loppuun.

Ranskalaisen pelin ratkaisu

[muokkaa | muokkaa wikitekstiä]

Jos ranskalaisella laudalla jätetään aluksi vain yksi reikä tyhjäksi, vain osa rei'istä on sellaisia, että tehtävä on mahdollista ratkaista jättämällä laudalle lopuksi vain yksi nappula. Sellaisia ovat vain seuraavissa kuvioissa esitetyt sekä ne, joissa alkuasema on yhtenevä näistä jonkin kanssa.

1) 

          0 1 2 3 4 5 6
        0     o · ·
        1   · · · · ·
        2 · · · · · · ·
        3 · · · · · · ·
        4 · · · · · · ·
        5   · · · · ·
        6     · · ·

Mahdollinen ratkaisu: [2:2-0:2, 2:0-2:2, 1:4-1:2, 3:4-1:4, 3:2-3:4, 2:3-2:1, 5:3-3:3, 3:0-3:2, 5:1-3:1, 4:5-4:3, 5:5-5:3, 0:4-2:4, 2:1-4:1, 2:4-4:4, 5:2-5:4, 3:6-3:4, 1:1-1:3, 2:6-2:4, 0:3-2:3, 3:2-5:2, 3:4-3:2, 6:2-4:2, 3:2-5:2, 4:0-4:2, 4:3-4:1, 6:4-6:2, 6:2-4:2, 4:1-4:3, 4:3-4:5, 4:6-4:4, 5:4-3:4, 3:4-1:4, 1:5-1:3, 2:3-0:3, 0:2-0:4]

2) 

          0 1 2 3 4 5 6
        0     · · ·
        1   · · o · ·
        2 · · · · · · ·
        3 · · · · · · ·
        4 · · · · · · ·
        5   · · · · ·
        6     · · ·

Mahdollinen ratkaisu: [1:1-1:3, 3:2-1:2, 3:4-3:2, 1:4-3:4, 5:3-3:3, 4:1-4:3, 2:1-4:1, 2:6-2:4, 4:4-4:2, 3:4-1:4, 3:2-3:4, 5:1-3:1, 4:6-2:6, 3:0-3:2, 4:5-2:5, 0:2-2:2, 2:6-2:4, 6:4-4:4, 3:4-5:4, 2:3-2:1, 2:0-2:2, 1:4-3:4, 5:5-5:3, 6:3-4:3, 4:3-4:1, 6:2-4:2, 3:2-5:2, 4:0-4:2, 5:2-3:2, 3:2-1:2, 1:2-1:4, 0:4-2:4, 3:4-1:4, 1:5-1:3, 0:3-2:3]

and 3) 

          0 1 2 3 4 5 6
        0     · · ·
        1   · · · · ·
        2 · · · o · · ·
        3 · · · · · · ·
        4 · · · · · · ·
        5   · · · · ·
        6     · · ·

Mahdollinen ratkaisu: [2:1-2:3, 0:2-2:2, 4:1-2:1, 4:3-4:1, 2:3-4:3, 1:4-1:2, 2:1-2:3, 0:4-0:2, 4:4-4:2, 3:4-1:4, 6:3-4:3, 1:1-1:3, 4:6-4:4, 5:1-3:1, 2:6-2:4, 1:4-1:2, 0:2-2:2, 3:6-3:4, 4:3-4:1, 6:2-4:2, 2:3-2:1, 4:1-4:3, 5:5-5:3, 2:0-2:2, 2:2-4:2, 3:4-5:4, 4:3-4:1, 3:0-3:2, 6:4-4:4, 4:0-4:2, 3:2-5:2, 5:2-5:4, 5:4-3:4, 3:4-1:4, 1:5-1:3]

Erilaisia pelilautoja

[muokkaa | muokkaa wikitekstiä]

Lauta­pasianssia on pelattu useilla eri kokoisilla peli­laudoilla, joskin edellä esitetyt kaksi ovat suosituimpia. Sitä on myös pelattu kolmiomaisella laudalla, joissa hypyt on sallittu kaikkiin suuntiin. Tehtävä on toden­näköisesti ratkaistavissa, jos sillä on sopiva "pariteetti" ja jos pelilauta on tarpeeksi laaja.

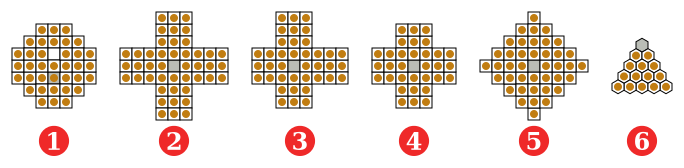
Erilaisia lautapasianssin lautoja:
(1) Ranskalainen (eurooppalainen), 37 reikää, 1600-luvulta;
(2) J. C. Wiegleb, 1779, Saksasta, 45 reikää;
(3) Epäsymmetrinen 3-3-2-2, jonka esitti George Bell 1900-luvulla;
(4) Englantilainen (standardi), 33 reikää;
(5) Timantti, 41 reikää;
(6) Kolmiomainen, 15 reikää.
Harmaa = reikä, johon viimeinen nappula jää.

Kolmiomaisessa muunnelmassa on viisi nappulaa reunalla. Jos aluksi jätetään tyhjäksi jokin kolmesta keskimmäisestä reiästä, peli ei ole ratkaistavissa niin, että viimeinen nappula jää samaan reikään. Jos aluksi jätetään kolmion kärjessä oleva reikä tyhjäksi, tehtävä on ratkaistavissa kymmenellä siirrolla, ja jos tyhjä reikä on kolmion sivulla, yhdeksällä siirrolla.[6]

Pelistä on olemassa myös shakkilaudalla pelattava muunnelma, jossa nappuloita asetetaan vain mustille ruuduille ja niistäkin yksi jätetään tyhjäksi. Siinä nappulat hyppäävät viistoon toisen nappulan yli sen toisella puolella olevaan tyhjään mustaan ruutuun.[2]

Käännös suomeksi
Käännös suomeksi
Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Peg solitaire

Lähteet

[muokkaa | muokkaa wikitekstiä]
  1. ↑ a b c Barb Whiter: ”Lautapasianssi”, Kodin suuri pelikirja, s. 171. Suomentanut Riitta Bergroth. Gummerus, 2002. ISBN 951-20-6140-6
  2. ↑ a b c d e f g Reijo Ahtokari, Kerttu Varjo, Keijo Voudinmäki: ”Erakkopelit”, Mitä Missä Milloin Ongelmakirja, s. 129-131. Otava, 1969.
  3. ↑ Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Winning Ways for your Mathematical Games, 4. osa. New York: Academic Press, 1982. 1-56881-144-6
  4. ↑ Mathematics and brainvita (Arkistoitu – Internet Archive)
  5. ↑ Solitaire - Solution and Notation topaccolades.com. Viitattu 10.12.2014.
  6. ↑ Solving triangular peg solitaire. Journal of Integer Sequences, 2008, nro 11. arXiv:math.CO/0703865

Kirjallisuutta

[muokkaa | muokkaa wikitekstiä]
  • On the solitaire cone and its relationship to multi-commodity flows. Mathematical Programming, 2001, nro 90, s. 27–57. doi:10.1007/PL00011419
  • John D. Beasley: The Ins & Outs of Peg Solitaire. Oxford University Press, 1985. ISBN 978-0198532033
  • A solitaire game and its relation to a finite field. Journal of Recreational Mathematics, 1968, nro 1, s. 121–123.
  • Mathematical Games. Scientific American, kesäkuu 1962, nro 206 (6).
  • Mathematical Games. Scientific American, helmikuu 1966, nro 214 (2).
  • Mathematical Games. Scientific American, toukokuu 1966, nro 207 (5).
  • Integer programming based algorithms for peg solitaire problems, Proc. 2nd Int. Conf. Computers and Games (CG 2000). Lecture Notes in Computer Science, 2001, nro 2063, s. 229–240. doi:10.1007/3-540-45579-5_15 .
  • Generalized Hi-Q is NP-complete. Trans. IEICE, 1990, nro 73, s. 270–273. .


Aiheesta muualla

[muokkaa | muokkaa wikitekstiä]
Wikimedia Commonsissa on kuvia tai muita tiedostoja aiheesta Lautapasianssi.
Noudettu kohteesta ”https://fi.wikipedia.org/w/index.php?title=Lautapasianssi&oldid=22790938”