Lujuusoppi
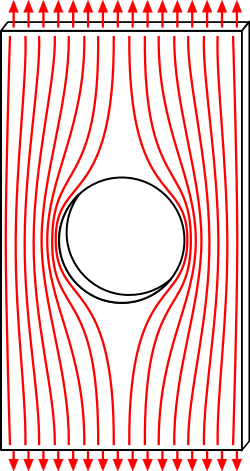
Lujuusoppi eli kiinteän aineen mekaniikka on jatkuvan aineen mekaniikkaan kuuluva fysiikan ala, jossa tutkitaan kiinteiden kappaleiden käyttäytymistä ulkoisten ja sisäisten kuormien vaikuttaessa niihin. Yleensä lujuusopin alaan luetaan kuuluvaksi myös esimerkiksi värähtelymekaniikka, materiaalin väsyminen ja murtumismekaniikka.
Suppeassa mielessä lujuusopin piiriin katsotaan kuuluviksi ainakin rakenteiden muodonmuutokset ja tästä suoraan saatavat rakenteen venymä ja edelleen jännitys.
Lujuusopin peruslause
[muokkaa | muokkaa wikitekstiä]- Jäykän kappaleen ollessa tasapainossa on kaikkien siihen vaikuttavien voimien oltava keskenään tasapainossa.[1]
- Kun kimmoisa kappale on tasapainossa, on sen jokaisen osan oltava tasapainossa.[1]
Yleinen muodonmuutostila
[muokkaa | muokkaa wikitekstiä]Rakenteen muodonmuutoksilla tarkoitetaan sen muodon vääristymistä, mutta myös sen paikan ja/tai asennon muutosta. Muodonmuutoksen voi aiheuttaa mekaaninen kuorma, mutta myös esimerkiksi lämpökuorma voi niitä aiheuttaa.
Muodonmuutokset voidaan jakaa jäykän kappaleen liikkeisiin ja muodon vääristymiin. Yleensä kappaleen kokonaismuodonmuutos on yhdistelmä näsitä molemmista.
Jäykän kappaleen liikkeessä kappale liikkuu (translaatio) tai pyörii (rotaatio) muuttamatta muotoaan. Jäykän kappaleen liikkeessä kaikki kappaleen pisteet pysyvät samalla kohtaa toistensa suhteen samassa, liikkuvassa koordinaatistossa (siirtymävektorien derivaatta on kaikkialla kappaleessa nolla). Tämän johdosta jäykän kappaleen liike ei aiheuta siihen myöskään venymiä tai jännityksiä. Esimerkiksi ilmaan heitetty kivi on likimain jäykkä kappale ilmalentonsa aikana (sen paikka ja asento muuttuu, mutta muoto säilyy).
Muodon vääristymisessä kappaleen pisteet liikkuvat toistensa suhteen siten, että sen muoto muuttuu. Vääristyminen voidaan jakaa kahteen osaan:
- Tilavuuden muutos (dilataatio), jossa kappaleen tilavuusalkion tilavuus muuttuu. Esimerkiksi pesusienen puristaminen kasaan joka suunnalta samassa suhteessa vastaa likimain tätä tapausta.
- Leikkautuminen. Esimerkiksi maassa kiinni olevan kumipalan yläpinnan työntäminen vaakatasossa aiheuttaa kumipalan leikkautumista.
Venymä
[muokkaa | muokkaa wikitekstiä]Venymä mittaa tilavuusalkion muodon vääristymisen suuruutta alkuperäiseen tilanteeseen verrattuna. Näin ollen jäykän kappaleen liikkeet eivät vaikuta venymiin. Venymä on materiaalista riippumaton, dimensioton vektorisuure ([m/m]), joka saadaan pienten siirtymien tapauksessa ottamalla derivaatta muodonmuutostilasta eri suunnissa käytettävien koordinaattiakselien suhteen. Näin saatava, kolmiulotteisessa tapauksessa dimensioiltaan 3x3 muodonmuutosmatriisi ilmaisee yksikäsitteisesti tilavuusalkion vääristymän. Siitä voidaan johtaa esimerkiksi paikallinen rakenteen tilavuuden muutos, leikkautuminen, venymät ja leikkautumat halutuissa suunnissa ja esimerkiksi päävenymät. Päävenymät saadaan kiertämällä tarkastelukoordinaatistoa siten, että kyseisessä suunnassa leikkautumat häviävät.
Pienillä venymillä yleensä riittävä, lineaarinen tekninen venymä saadaan yksiulotteisessa tapauksessa jakamalla kappaleen pituuden muutos sen alkuperäisellä pituudella: .
Venymän ja jännityksen välinen yhteys
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Jännitys-venymäkäyrä
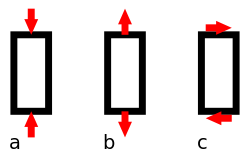
Tämä konstitutiivinen yhteys liittää toisiinsa venymä- ja jännitysvektorit. Jos yhteys on lineaari (materiaalin elastisuus), on kyseessä (yleistetty) Hooken laki. Tällöin saadaan jännitysvektori suoraan kertomalla venymävektori kimmomatriisilla ja edelleen esimerkiksi ulkoiset kuormat selvittämällä kuormien tasapainon toteuttavat tukireaktiot kappaleen reunoilla. Ottamalla kimmomatriisista käänteismatriisi, nk. joustomatriisi ja kertomalla tällä jännitysvektori, voidaan puolestaan selvittää paikalliset venymät. Ottamalla venymistä integraali rakenteen yli voidaan puolestaan selvittää koko rakenteen muodonmuutostila. Ratkaisuun tarvitaan myös yhteensopivuus l. kompabiliteettiehtoa, joilla huomioidaan se, että venymät eivät voi olla täysin mielivaltaisia, vaan eri venymäkomponenttien on oltava keskenään yhteensopivia.
Yleisessä tapauksessa venymän ja jännityksen välinen yhteys ei kuitenkaan ole lineaari tai edes yksikäsitteinen. Esimerkiksi plastinen materiaali myötää tietyn materiaalista riippuvan jännitystason jälkeen, ja kuorman poistuessa rakenteeseen jää pysyviä venymiä (ja näitä vastaavia jäännösjännityksiä). Pysyvillä venymillä tarkoitetaan useimmiten tässä yhteydessä rakenteeseen jääviä muodonmuutoksia, jotka eivät poistu kuorman poistuessa. Esimerkiksi kestomuovit ovat usein hyvin plastisia.
Materiaali voi myös murtua. Haurailla aineilla tämä tapahtuu lähes samalla venymällä kuin myötäminen.
Virumisella ymmärretään venymien kasvamista ajan mukana vakiokuormallakin.
Materiaalien käyttäytymiselle kuormitettuna on lukuisia muitakin mahdollisuuksia. Materiaalien mekaanista käyttäytymistä tutkii kokonaan oma tieteenalansa, materiaalioppi.
Lujuushypoteesi
[muokkaa | muokkaa wikitekstiä]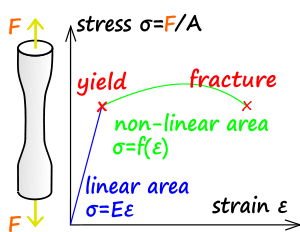
Lujuushypoteesi on teoria joka ennustaa, kestääkö materiaali jonkin jännitystilan vaurioitumatta.
Rakenteen paikallinen jännitys- ja venymätila ovat vektorisuureita. Materiaalin lujuuteen liittyvät lujuusarvot, kuten esimerkiksi materiaalin myötämisen aiheuttava jännitys (myötöraja) tai murtumisen aiheuttava murtoraja ilmaistaan kuitenkin usein vain yhdellä, esimerkiksi vetosauvalla tehtyjen vetokokeiden perusteella saadulla materiaaliarvolla, eli skalaarilla. Lujuushypoteeseillä todellisesta jännitys- (tai venymä)vektorista muodostetaan skalaari vertailujännitys, jota verrataan vetokokeen tulokseen. Jos vertailujännitys ylittää kyseisen materiaaliarvon, pettämisen oletetaan tapahtuvan. Lujuushypoteesi siis yksinkertaistaa todellisen jännitystilanteen ja tarjoaa yksinkertaisen tavan vertailla materiaalin kokemaa jännitystä materiaalitestien tuloksiin.
Yleisimpiä jännityshypoteesejä ovat maksimipääjännitys-, maksimipäävenymä-, maksimileikkausjännitys (Tresca), vakiomuodonmuutosenergia- ja vakiomuodonvääristymisenergia (von Mises)-hypoteesit. Nykyään useimmiten käytetään von Misesin tai Trescan kriteeriä sitkeille aineille, kuten teräs. Hauraille aineille (valurauta, betoni) käytetään myös pääjännitys- ja päävenymähypoteesejä.
Komposiittimateriaaleilla, joiden lujuus vaihtelee kuormitussuunnasta riippuen, on omia lujuushypoteesejään.
Rakenteiden vaurioituminen
[muokkaa | muokkaa wikitekstiä]Rakenteessa oleva materiaali voi joutua niin kovan jännityksen alaiseksi että siinä tapahtuu vaurioituminen. Tällöin on kyseessä materiaalin lujuuden ylittyminen. Myös materiaalin kyky kestää väsyttävää kuormitusta tai virumista voi ylittyä. Kuitenkin tarkasteltaessa rakennetta kokonaisuutena se voi vaurioitua myös stabiliteetin menettämisen johdosta. Stabiliteetin menettämisen tapoja ovat esimerkiksi nurjahdus, lommahdus ja kiepahdus. Käytännössä aina seurauksena on lisäksi myös pysyviä vaurioita rakenteeseen, jotka johtuvat materiaalin lujuuden ylittymisestä.
Lujuusopin käsitteitä
[muokkaa | muokkaa wikitekstiä]Keskeisiä lujuusopin käsitteitä ovat:
- taipuma
- siirtymä
- pituuden muutos
- venymä (myötymä)
- painopiste
- nurjahdus, lommahdus
Lujuusopin suureita ja yksiköitä
[muokkaa | muokkaa wikitekstiä]- jänneväli (yksikkö m)
- poikkipinta-ala (yksikkö m²)
- kimmokerroin eli kimmomoduuli (E, yksikkö N/m²)
- normaalivoima (yksikkö N)
- leikkausvoima (yksikkö N)
- taivutusmomentti (M, yksikkö Nm)
- taivutusvastus (W, yksikkö m³)
- jäyhyysmomentti (=jäyhyys; I, yksikkö m4)
- jännitys (σ, yksikkö N/m²)
- kuormitustiheys (yksikkönä N/m)
Lähteet
[muokkaa | muokkaa wikitekstiä]- Pennala, Erkki: Lujuusopin perusteet. Moniste 407, Otatieto 1992, Espoo.
